Применение математического моделирования в менеджменте

В эпоху глобального научно-технического прогресса, а также беспощадной конкуренции - менеджер обязан владеть математическими методами, а также инструментами для количественного анализа состояния и прогнозирования развития социально-экономических систем разного уровня, для моделирования инвестиционных процессов, а также для оценки рисков управленческих решений.

Однако на данный момент профессиональные характеристики управленца не включают в себя профессиональное владение экономикоматематического анализа, а предполагает лишь поверхностное знание о том, как влияет математика на решение тех или иных вопросов. Математические методы абсолютны универсальны, применить их можно в любой сфере жизнедеятельности человека, именно поэтому они так важны в области менеджмента.

Двигатель национального развития - конкуренция всех имеющихся ресурсов (материальных или интеллектуальных). Для того, чтобы быть готовым к конкурентной борьбе организаций - менеджер должен уметь принимать моментальные, а главное, эффективные управленческие решения в сложно ситуации, нестандартно мыслить, уметь независимо выявлять проблемы, а также их причины, прогнозировать дальнейшее развитие данной проблемы, а также четко видеть пути ее решения. [1] Менеджер в наши дни - универсальный специалист, знающий все отрасли развития своего предприятия:  состояние исследований, техники, конкуренции, динамики рынка, спроса на продукцию. Но он не сможет все это проанализировать, не владея математической основой.

Назовем две основные проблемы, в области обучения «Менеджмент»:

Первое, что необходимо отметить: при всех высказываниях и переизбытке менеджеров на рынке труда, квалифицированных специалистов недостаточно. На самом деле, в учебном плане многих образовательных учреждений не предусмотрен тот факт, что каждая организация имеет свою природу, а, соответственно, различного характера управленческие задачи.

Второе - равнодушное отношение многих организаций и самих менеджеров к математической подготовке. Уровень их обучения, к сожалению, не позволяет быть максимально эффективным в организации. [4].

В последнее время заметно изменились запросы к профессиональной подготовке менеджеров всех уровней. Современный менеджер обязан не только владеть знаниями и умениями в рамках свой профессиональной подготовки, но и уметь применять их, а самое главное, решать те или иные задачи компании с помощью этих навыков.

На сегодняшний день существует множество возможностей внедрения математического моделирования, как инструмента управления - в сферу менеджмента.

Одной и той же математической моделью можно воспользоваться для решения нескольких задач, которые одинаковы по своей управленческой природе, но абсолютно разные по экономическому смыслу.

Наглядный пример - классификация В.Е. Глизнуцина, которая позволяет решать задачи менеджмента, с помощью каких-либо математических моделей. [2]

Соответственно, применение какого-либо метода определяет вид задачи.

Примеры (Таб.1)

Таблица 1. Соответствие конкретной математической модели конкретным задачам управления

Математическая модель	Применение
Теоретические модели	Модель непрерывного начисления процентов
Балансовые модели	Модель международной торговли
Макроэкономические модели	Модель   межотраслевого   баланса   В. Леонтьева
Микроэкономические модели	Модель «затраты-выпуск» для конкретного экономического объекта

Однако необходимо отметить, что существует несколько мнений о математическом моделировании, поэтому развернутой классификации математических моделей не существует. С развитием в данной области вопрос классификации только усугубляется, так как появляются новые типы математического моделирования, а также новые признаки их классификации.

Имея некий багаж знаний, а также умение применять математическое моделирование-менеджер без затруднений оценит текущее положение компании, также выявит причины, из-за которых сложилось данное положение и сможет найти пути решения.

В современном обществе все больше и больше стирается грань между подчиненным и управляющим. Вместе с переходом от преимущественно -функционального к процессному управлению - изменились и запросы к профессиональным требованиям управленца. Теперь для качественного и продуктивного выполнения своих функций - менеджер должен расширять свой круг навыков и умений, быть более грамотным в использовании новейших инструментов управления. Управленец - это не власть, а полномочия. [6]

По мнению А. М. Лялина, будущих выпускников по направлению «Менеджмент» необходимо готовить к жесткой конкурентной борьбе своих организаций, а успех в данной борьбе будет основан на оптимизации использования ограниченных ресурсов, высокой экономической культуре, спланированной концепции развития компании. Всех этих аспектов успеха компании можно добиться посредством математических моделей. [3] Следует выделять не менее четырех компонент, за которые отвечает непосредственно менеджер, представляющие собой единый комплекс политик, реализуемых любой современной компанией, стремящейся обеспечить себе устойчивое стратегическое лидерство в быстроменяющихся условиях: кадровая, финансовая, маркетинговая, технологическая. В любой из них математическая основа просто необходима.

Рассмотрим пример на модели теории фирм, рынка.

Пусть y(t) - интенсивность выпуска продукции некоторого предприятия. Предполагается , что с увеличением выпуска происходит насыщение рынка и цена товара р (у) падает. Пусть, например, р (у)= b-ay (a,b>0) и скорость увеличения интенсивности выпуска продукции является возрастающей функцией дохода. [4]

Составляем дифференциальное уравнение для функции y(t) и, решив его, построим график этой функции .

dy

Согласно механическому смыслу производной у =— есть скорость dt изменения функции y(t.) По условию — = k(b - ay)y, dt где р(у)у - доход от продажи выпуска y(t) по цене р(у).

dy Разделяя переменные, получим уравнение------- = kdt ,

У ⁽ b ^- ay )

Cbebkt интегрируя которое находим У =;—-—ти.

• 1    + Cae

Полученная в результате интегрирования функция y(t) представляет собой уравнение так называемой логистической кривой, часто возникающей в различных разделах экономических наук.

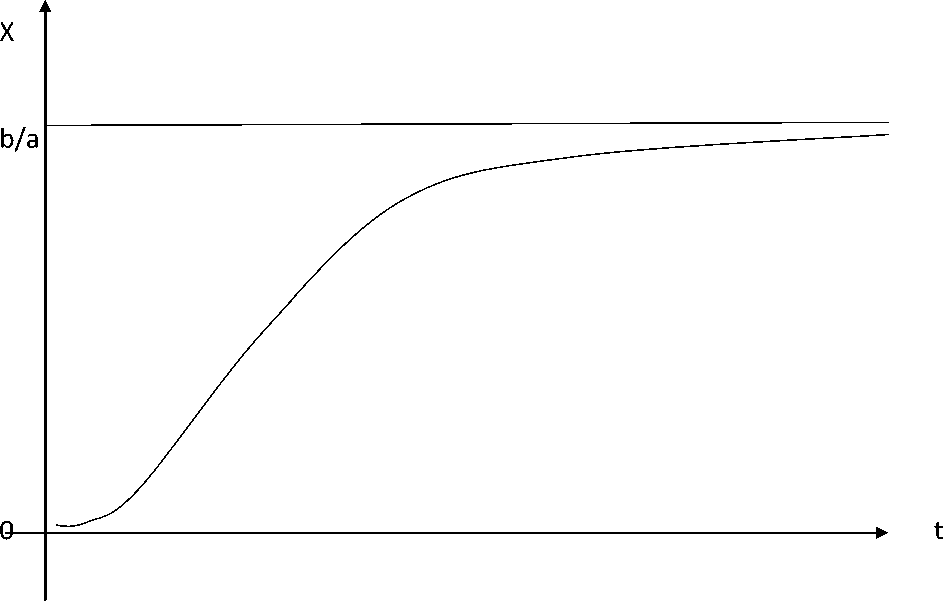
Логистическая кривая в данном случае отражает характер поведения выпуска продукции y(t) в соответствии с условием задачи, а именно на лицо насыщение рынка товаром с ростом времени t. [5]

Владение знаниями в области математического моделирования помогает не только развить целый ряд имеющихся навыков, но и приобрести новые. Тут же необходимо отметить, что для менеджера математическое моделирование не является основой его деятельности, оно выступает в качестве агрегата, которым можно воспользоваться.

Таким образом, можно сделать вывод: вряд ли высококвалифицированный менеджер возможен без какой-либо фундаментальной подготовки, а особенно в сфере математического моделирования.