Применение математического пакета для разработки и визуализации решения задачи аналитической геометрии с параметром

Автор: Копотева А.В., Затонский А.В., Мамаев Д.А.

Журнал: Вестник Южно-Уральского государственного университета. Серия: Компьютерные технологии, управление, радиоэлектроника @vestnik-susu-ctcr

Рубрика: Информатика и вычислительная техника

Статья в выпуске: 3 т.25, 2025 года.

Бесплатный доступ

Данная работа посвящена изучению вопроса возможности применения математического пакета Mathcad 15.0 для решения задач аналитической геометрии с параметрами. Обзор отечественных и зарубежных источников показал, что при всем разнообразии применения различных математических пакетов для решения задач с параметрами их почти не используют. Цель исследования: изучение возможности применения математического пакета для решения задач аналитической геометрии с параметрами, что позволит не только избежать арифметических и прочих ошибок, свойственных человеку, но и получить инструмент генерации различных вариантов одной и той же задачи и шаблон для проверки соответствующих работ учащихся. Материалы и методы. Исследование выполнено в среде Mathcad 15.0 на примере решения задачи взаимного расположения прямой и эллипса с переменной ординатой центра симметрии. Были рассмотрены два различных способа аналитических решений задачи и выполнена реализация одного из них в среде Mathcad. Аналитическое решение задачи взаимного расположения прямой и кривой второго порядка с параметром возможно либо путем анализа числа их общих точек на основании выраженных через параметр координат, либо путем нахождения координат точки касания на основании равенства угловых коэф¬фициентов прямой и касательной к кривой в точке касания. Результаты. В рамках данного исследования установлено, что Mathcad позволяет как реализовать оба аналитических метода решения задачи, так и непосредственно найти выражения для координат точки касания в зависимости от параметра путем решения системы нелинейных уравнений и затем исследовать их на принадлежность множеству действительных чисел. Заключение. Проведенное нами исследование позволяет утверждать, что Mathcad позволяет реализовать различные варианты решения задачи аналитической геометрии с параметром и сделать соответствующую графическую интерпретацию результата. Полученное решение может быть использовано для составления различных вариантов задачи с решением из области рациональных чисел, проверки полученных студентами результатов, а также в качестве образца выполнения задания.

Еще

Аналитическая геометрия, эллипс, прямая, задача с параметром, точка касания, Mathcad

Короткий адрес: https://sciup.org/147251611

IDR: 147251611 | DOI: 10.14529/ctcr250302

Текст научной статьи Применение математического пакета для разработки и визуализации решения задачи аналитической геометрии с параметром

Математические задачи с параметром из школьной или университетской программы в силу своих сложности и нетривиальности оказываются подходящим инструментом организации научноисследовательской работы студентов младших курсов. Однако использование таких задач в учебном процессе сопровождается целым рядом сложностей. Помимо непосредственной формулировки задачи на естественном языке преподавателю необходимо, во-первых, обеспечить достаточное число вариантов в соответствии с количеством студентов, во-вторых, подобрать такие числовые величины в ней, чтобы результаты расчетов оказались приемлемыми, в-третьих, разработать и реализовать метод решения, подходящий для проверки решения задачи студентом, и, в-четвертых, визуализировать полученные результаты. При этом само решение задачи с параметром зачастую приводит к набору взаимосвязанных задач различной сложности, часто не имеющих аналитического решения. В связи с перечисленными проблемами возникает необходимость выбора инструментального средства, позволяющего решить их хотя бы частично. Естественно, реализация одного и того же метода решения задачи с использованием различных математических пакетов может существенно различаться, а решение любой задачи в рамках конкретного пакета является прикладной задачей, имеющей собственную специфику и сложности. В рамках данной работы выполнена оценка возможностей среды Mathcad 15.0 для разработки и реализации метода решения задач с параметром на примере задачи исследования взаимного расположения прямой и кривой второго порядка в зависимости от параметра одной из них.

Обзор исследований, посвященных решению задач с параметрами, привел к неожиданным результатам. Вопросы необходимости и преимуществ применения программных средств в образовании поднимаются в [1] (на примере Mathcad), [2] (на примере Wolfram Mathematica) и [3] (на примере Matlab), однако нам не удалось обнаружить исследований, посвященных решению задач с параметрами из школьной или университетской программы. Русскоязычные авторы уделяют существенное внимание решению задач с параметрами из школьной программы в рамках подготовки к ЕГЭ. В частности, существуют статьи, посвященные решению геометрических [4] и тригонометрических [5] задач с параметрами, а также методам решения таких задач [6]. В отдельных исследованиях рассматриваются вопросы применения программных продуктов для решения задач школьной программы с параметром, в частности, Mathcad [7] и Wolfram alpha [8]. Несколько более широко как в отечественных, так и зарубежных изданиях представлены исследования, посвященные использованию программных средств для решения теоретических и прикладных задач. Применение пакета Mathcad для визуализации в задачах аналитической геометрии рассматривается в работах [9, 10]. Решение и визуализации задач начертательной геометрии средствами Wolfram Mathematics описаны в [11], применение его для построения линии пересечения поверхностей второго порядка – в [12]. Построение в среде Matlab поверхностей каналов теплообменных устройств реализовано в [13]. Проблеме программной визуализации и анимации на примере параметрических кривых Безье посвящено исследование [14]. Моделирование в среде Mathcad поведения идеальных материалов выполнено в [15].

Достаточно широко представлены прикладные задачи с параметрами, например, посвященные исследованию температуры стальных конструкций под действием солнечной энергии [16] и применению балансовой модели популяции для симуляции процесса кипения в смеси двух жидкостей [17]. Кроме того, большое внимание уделяется математическим задачам с параметрами: алгебраическим (решение общих нелинейных задач нахождения собственных значений матриц [18]), математического анализа (решение общих линейных эллиптических уравнений в частных производных второго порядка [19]), вариационного исчисления [20]. Таким образом, нам не удалось найти статей, посвященных решению задач аналитической геометрии с параметрами с использованием математических пакетов. Проблема является весьма актуальной как для преподавателя по причинам, перечисленным ранее, так и для студентов, поскольку попытка выполнить соответствующее задание вызвала у них существенные затруднения. Это означает, что успешная разработка и реализация метода решения задачи с параметром с использованием математического пакета полезны не только для преподавателя с точки зрения разработки и проверки студенческих работ, но и для студентов в качестве образца выполнения таких заданий, что и определяет актуальность данной работы.

Выполним решение задачи аналитической геометрии на взаимное расположение прямой и кривой второго порядка средствами Mathcad 15.0. Параметром может выступать любой из коэффициентов уравнений прямой или кривой второго порядка. Для определенности сформулируем задачу следующим образом: требуется исследовать взаимное расположение эллипса с центром в точке М (–1; y 0 ) и полуосями а = 4 и b = 3 и прямой 5· x – 16· y – 32 = 0 в зависимости от значения параметра у 0 , определить координаты общих точек, если они есть, и построить графики.

1. Визуализация задачи средствами Mathcad 15.0
2. Решение задачи взаимного расположения прямой и эллипсапутем определения их общих точек

Каноническое уравнение эллипса с центром в точке М ( x 0 ; y 0 ) и полуосями а > 0 и b > 0 имеет вид ( x – x 0 )²/ a ² + ( y – y 0 )²/ b ² = 1, причем явной однозначной зависимости между абсциссой и ординатой в данном случае на существует. Построение графика кривой в неявном виде в Mathcad 15.0 невозможно, поэтому введем замену переменных ( x – x 0 )/ a = cos( t ), ( y – y 0 )/ b = sin( t ) и перейдем к параметрическим уравнениям эллипса x = x 0 + a ·cos( t ), y = y 0 + b ·sin( t ). Тогда в нашем случае эллипс с центром симметрии в точке М (–1; y ₀), полуосями а = 4 и b = 3 описывается уравнением ( x + 1)²/4² + ( y – y 0 )²/3² = 1 или в параметрической форме x = –1 + 4·cos( t ), y = y 0 + 3·sin( t ). Изменение ординаты центра эллипса y 0 приводит к его параллельному переносу по вертикали (рис. 1).

Прямая 5· x – 16· y – 32 = 0 задана общим уравнением, т. е. тоже неявно, однако в данном случае можно получить явное уравнение y = 5· x /16 – 2. Визуальный анализ возможных взаимных расположений прямой и эллипса при различных значениях параметра y 0 (см. рис. 1) позволяет заключить, что кривые могут иметь n = 0, 1, 2 общих точек.

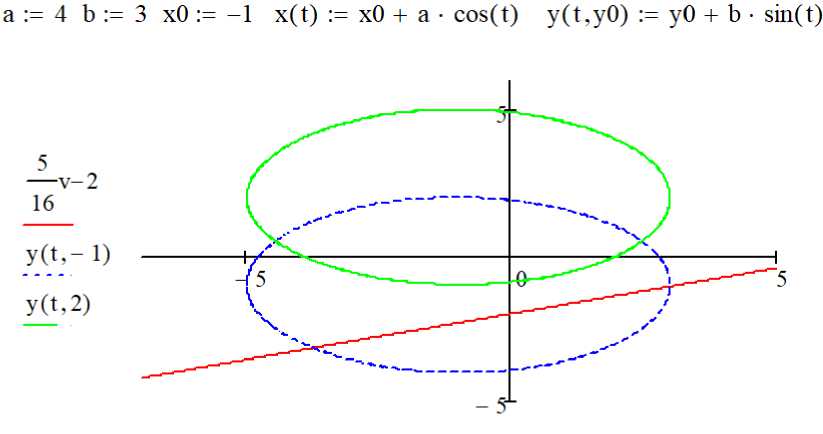
v,x(t) ,x(t) ,x(t)

Рис. 1. Графики эллипса ( x + 1)²/4² + ( y – y 0 )²/3² = 1 и прямой 5· x – 16· y – 32 = 0 при различных значениях параметра y 0

Fig. 1. Ellipse ( x + 1)²/4² + ( y – y 0 )²/3² = 1 and the straight line 5· x – 16· y – 32 = 0 graphics for different values of parameter y 0

Формально координаты общих точек могут быть найдены путем решения системы

⁽ x + 1) 2 , ⁽ У - У 0 ) 2

<42 32 ;(1)

5 ■ x - 16 ■ у - 32 = 0.

Полученная система является нелинейной, при подстановке в первое уравнение явного выражения для у получается квадратное уравнение для x с параметром вида

.169■ x2 - 120+1 .x + *02. + ±А-21 = 0.(2)

2304 72 9 9144

Найдем выражение для дискриминанта квадратного уравнения (2) и разложим его на простые множители:

D = - у 02 /36 - 37- у о /288 + 445/3072 = (15-16- у о )-(16- у о + 89)/9216.

Тогда x 1,2 = 1152<(5- у о + 1)/72 ± D) )/169.

Очевидно, уравнение (2) не имеет действительных коней при D < 0, имеет действительный корень кратности 2 при D = 0 и пару различных действительных корней при D > 0.

Разложение дискриминанта на простые множители позволяет установить, что D = 0 при у ₀ i = 15/16 и у ₀₂ = -89/16, т. е. при соответствующих значениях параметра система (1) имеет единственное решение, а прямая и эллипс - единственную общую точку (рис. 2). Найдем ее координаты при у ₀₁ = 15/16:

x1 = 1152-(5-15/16 + 1)/72)/169 = 7/13, тогда у 1 = 5/16-7/13 - 2 = -381/208,

т. е. точкой касания эллипса и прямой будет M 1 (7/13; -381/208). При у ₀₂ = -89/16

x 2 = 1152-(-5-89/16 + 1)/72)/169 = -33/13, тогда у 2 = 5/16-(-33/13) - 2 = -581/208,

т. е. точкой касания эллипса и прямой будет M 2 (-33/13; -581/208).

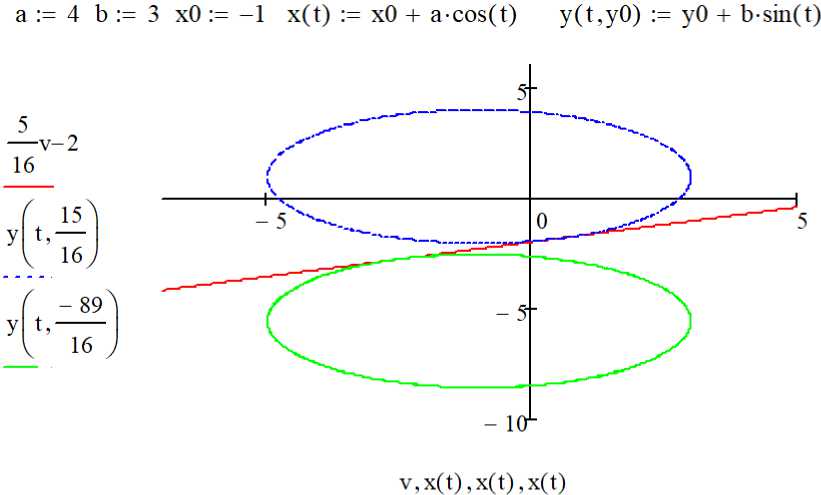
Рис. 2. Касание эллипса ( x + 1)²/4² + ( y – y 0 )²/3² = 1 и прямой 5∙ x – 16∙ y – 32 = 0

Fig. 2. Ellipse ( x + 1)²/4² + ( y – y 0 )²/3² = 1 and the straight line 5∙ x – 16∙ y – 32 = 0 points of contact

Если дискриминант положителен, т. е. (15 - 16^ у ₀у(16^ у о + 89)/9216 > 0, то система (1) имеет два решения, а прямая пересекает эллипс в двух точках. Решение полученного неравенства имеет вид -89/16 < у ₀< 15/16. Абсциссы точек пересечения определяются выражениями:

x 1,2 — 1152-((5- у о + 1)/72 ± 7 (15 -16 • у0) • (16 • у0 + 89)/9216 )/169, откуда x1 — 16/169 + 80-уо/169 + 12^ 7(15 -16 • у0) • (16 • у0 + 89) /169, x2—16/169 + 80;уо/169 - 12^ 7(15 -16 • у0) • (16 • у0 + 89) /169.

Ординаты точек пересечения равны соответственно у 1 — 5^x 1/16 - 2 — 5^(16/169 + 80;уо/169 + 12^ ^(15-16• у0)• (16• у0 + 89) /169)/16 - 2 —

— 25- у о /169 - 333/169 + 15^ ^(15 - 16 • у ₀) • (16 • у ₀ + 89) /676,

у 2 — 5^ x 2 /16 - 2 — 5^(16/169 + 80; у о /169 - 12^ ^(15 - 16 • у ₀) • (16 • у ₀ + 89) /169)/16 - 2 —

— 25- у о /169 - 333/169-15- ^(15 - 16 • у ₀) • (16 • у ₀ + 89) /676.
3. Решение задачи взаимного расположения прямой и эллипсапутем нахождения точки их касания

Если дискриминант отрицателен, т. е. (15 - 16- у 0)^(16' у0 + 89)/9216 < 0, то система (1) не имеет решений, а прямая не пересекает эллипс. Решение полученного неравенства имеет вид у о е (-да; -89/16) и (15/16; +да).

Задачу можно решить альтернативным способом, исходя из следующих соображений. В точке касания прямой и эллипса производная эллипса равна угловому коэффициенту касательной. Полученное равенство в совокупности с уравнениями прямой и эллипса дает систему трех уравнений с тремя неизвестными - искомым параметром и координатами точки касания.

В нашем случае производная эллипса находится по формуле производной неявной функции:

d	' ⁽ x ⁺ ^{1)2 (} у - у 0 ⁾²	=d-m => ² • ⁽ x ⁺ 1) । ² • ⁽ у ^- у 0 ) • у ‘ ₌₀ => x ⁺ ¹ 1 ² • ⁽ у ^- у 0 ) • у' =о =>
dx	[ 4² 3² ,	d x 16 9 8 9

, ² • ( У ^- У о ) • У' x + 1 x + 1 9 _ 9 x + 1

—> ------------- _--—> y — --• ---------- _--• ------ .

9 8 8 2 • ( у - у о ) 16 у - у о

Равенство полученной производной в точке касания угловому коэффициенту рассматриваемой прямой дает соотношение вида

9 x _K +1 5

к --.---------_---

¹⁶ y к - y 0 ¹⁶

или после преобразования

5·( y к – y 0 ) + + 9·( x к + 1) = 0.

Поскольку точка касания лежит на прямой

5∙ x – 16∙ y – 32 = 0,

то полученная пара равенств образует систему двух линейных уравнений с параметром вида

/5 • ( y к - y о ) + ⁹ • ( x к + 1) = 0;
5 • x_K - 16 • y_K - 32 = 0.

кк

Ее решение имеет вид xк = (80·y0 + 16)/169;

y к = (25· y 0 – 333)/169.

Подставляя полученные значения в уравнение эллипса, получаем квадратное уравнение относительно параметра y 0 вида

16· y 0 ²/169 + 74· y 0 /169 – 1335/2704 = 0.

Его решение дает пару действительных корней y01 = 15/16 и y02 = –89/16, совпадающих со значениями параметров, полученными выше. Подставляя полученные значения в выражения для координат точки касания, получаем x1 = (80·15/16 + 16)/169 = 7/13;

x 2 = (80·(–89/16) + 16)/169 = –33/13;

y 1 = (25·15/16 – 333)/169 = –381/208;

y 2 = (25·(–89/16)–333)/169 = –581/208.

Понятно, что при значениях параметра, отличного от найденных, прямая будет либо пересекать эллипс, т. е. иметь с ним пару общих точек, либо не пересекать его, т. е. не иметь с ним общих точек. В соответствии с рис. 1 можно утверждать, что при превышении параметром соответствующего значения в верхней точке касания, т. е. при y ₀ > 15/16, эллипс расположен выше прямой 5∙ x – 16∙ y – 32 = 0 и не имеет с ней общих точек. Аналогично при значениях параметра меньших, чем в нижней точке касания, т. е. при y 0 < –89/16, эллипс расположен ниже прямой 5∙ x – 16∙ y – 32 = 0 и также не имеет с ней общих точек. Соответственно, при –89/16 < y ₀< 15/16 прямая пересекает эллипс в двух точках. Координаты точек пересечения при этом придется искать как решение системы (1), причем случаи нулевого и отрицательного дискриминанта уравнения (2) можно не рассматривать.

Заметим, что все расчеты выполнены в Mathcad в силу громоздкости получаемых выражений.

Найдем координаты общих точек прямой и эллипса как решение соответствующей системы

Given	(х + 1) .		(у - уО) ------=1 5х-16у-32=0 9				2 ' 256-уО 16 169
	It	( 80-у0 169
			/ 2 /
			12 у 1335 - 1184-уО - 256 у0	16	80 у0 12 ^ 1335 - 1184-уО -
			169	169	169	169
Find(x	-у) ->
		25-уО	15-^ 1335 - 1184-уО - 256-уО²	333	25-уО 15 J1335 -	1184-уО -	256-уО² 333
		169	676	169	169	676	169 )

Определим значения параметра, при которых подкоренное выражение равно нулю уО1:= — 16

-=1 5х-16у-32=0

, (у-уО1)

, (У-У02)

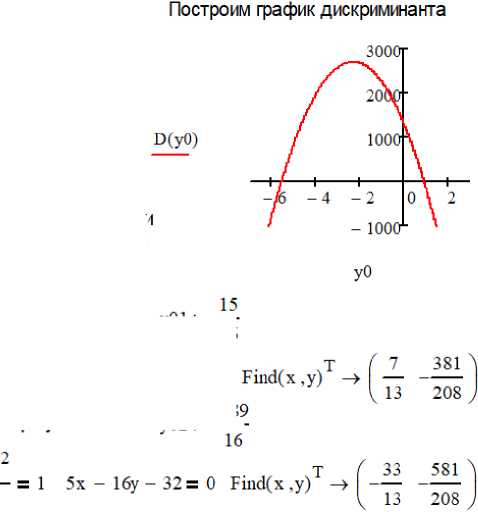
D(yO) := 1335 - 1184-уО - 256у0

Given D(yO) = О

Find(yO) —>

15 89

16 16

При положительном дискриминанте, те. при -89/16<у0<15/16, получаем две точки пересечения с координатами, найденным выие. При отрицательном дискриминантее, т.е. при у0<-89/16 и у0>15/16, прямая не пересекает эллипс.

Найдем координаты точки касания при у0=15/16

Given

Найдем координаты точки касания при у0=-89/16 _У02 := —

Given

Рис. 3. Решение задачи взаимного расположения эллипса ( x + 1)²/4² + ( y – y 0 )²/3² = 1 и прямой 5∙ x – 16∙ y – 32 = 0 в зависимости от параметра y 0 в среде Mathcad 15.0 Fig. 3. Relative position of ellipse ( x + 1)²/4² + ( y – y 0 )²/3² = 1 and straight line 5∙ x – 16∙ y – 32 = 0 problem solution depending on the parameter y 0 in Mathcad 15.0

Заключение

Приведенные в работе варианты решения задачи определения взаимного расположения эллипса и прямой в зависимости от ординаты центра эллипса позволяют убедиться возможности разработки различных способов решения задачи с параметром в соответствии с навыками и предпочтениями решающего ее лица и реализации этого способа в математическом пакете. При этом Mathcad оказывается не только удобным средством визуализации и решения задачи в рамках собственного функционала, но и незаменимым инструментом, позволяющим сконструировать различные варианты аналитического решения, автоматизировать арифметические вычисления и алгебраические преобразования с целью устранить соответствующие ошибки, подобрать числовые значения и их сочетания для обеспечения требуемого вида решения и генерации необходимого числа вариантов задачи. Это позволяет использовать его как удобную и гибкую среду разработки, реализации и проверки правильности методов решения различных задач с параметрами.

Статья научная