Применение математической регрессии для определения параметров трёхфазного асинхронного двигателя
Автор: Воржев Владимир Борисович, Калиенко Иван Викторович
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 5-6 (74) т.13, 2013 года.
Бесплатный доступ
Статистический разброс параметров электротехнических устройств часто является проблемой для анализа их работы и точного определения оптимальных режимов. В этих условиях требуются математические алгоритмы, позволяющие производить диагностику таких устройств с точностью, достаточной для инженерных расчётов. В настоящей работе предложен новый алгоритм расчёта характеристики момент-скольжение трёхфазного асинхронного двигателя. Он позволяет определить величины максимального момента и критического скольжения. Для этого статистически обрабатывается начальный участок характеристики, полученный экспериментальным путём. Этот в значительной степени универсальный метод решения подобных электротехнических задач базируется на общих математических подходах. В связи с этим он может быть положен в основу электронного диагностического устройства на базе микропроцессора.
Математическая регрессия, метод наименьших квадратов, характеристика момент-скольжение, диагностика электротехнических устройств
Короткий адрес: https://sciup.org/14250012
IDR: 14250012 | УДК: 519.6:621.313.333.045.53 | DOI: 10.12737/1284
Текст научной статьи Применение математической регрессии для определения параметров трёхфазного асинхронного двигателя
Введение. Применение сложной микропроцессорной техники позволяет создавать устройства диагностики электродвигателей, основываясь на минимальном количестве измерений. Их нехватка компенсируется сложными математизированными алгоритмами. На сегодняшний день это не повышает стоимости подобных приборов, но значительно упрощает для потребителя процедуру диагностики. Таким образом, соответствующее направление представляется актуальным. В настоящее время сформировались некоторые теоретические и практические подходы к вопросам диагностики электродвигателей, в том числе асинхронных [1—3]. Одно из таких решений представлено в настоящей статье.
-
1. Постановка задачи. Как известно, основной энергетической характеристикой трёхфазного асинхронного двигателя является характеристика момент-скольжение (рис. 1), выражаемая с достаточной точностью формулой Клосса [4].
-
2. Описание метода. Предлагаемый в данной статье метод основан на статистической обработке начального участка характеристики M ( s ) по методу наименьших квадратов (МНК) [5] с вычислением величин Mm и sкр . Как следствие, получаем теоретическую зависимость (1).
2М s s
M ( s ) = . (1)
кр
Как видно из (1), для её получения необходимо знать значения двух величин: максимального момента Mm и критического скольжения sкр . Эти величины известны не всегда. Их экспериментальное обнаружение затрудняет остановка двигателя при достижении им точки ( sKp , Mm ) . При теоретическом нахождении указанных величин сложность представляет определение параметров Т-образной схемы замещения. Таким образом, выяснив значения величин Mm и sкр , можно с достаточной точностью рассчитать все остальные точки рабочего участка кривой M ( s ).
Работа выполнена в рамках инициативной НИР.
Как известно [5], МНК основан на определении экстремума некоего функционала f ( 51, a2
,...,
a n ) = £ [ У экс;
— V meopi ( Хэкс; ) ] 2 ^ min,
где y3KCi — вектор экспериментальных значений функции, yTeopi ( x^ i ) — вектор теоретических (предполагаемых) значений этой функции с аргументами, полученными экспериментальным путём.
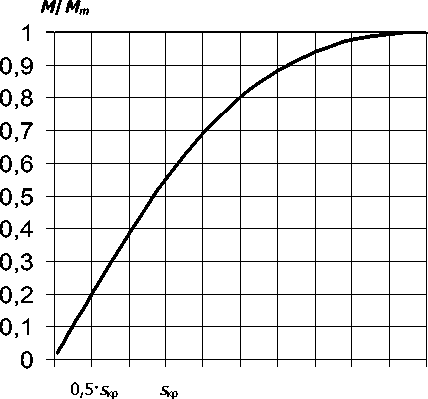
s ·100%
Рис.
1. Нормированная характеристика момент-скольжение
Сделаем некоторые преобразования в формуле (1):
22 кр
s
M(s} IM s s 2M s m кр m кр
Введём обозначения: — = a , s = b , —= y (s ). Mm " M ( S ) X '
+ s kp
2 M m s
.
Тогда
Из (2) следует, что
y(s)
as ab
=--1--.
2 b 2 s
f ( a , b ) = S V i
—
i
asi
2 b
—
ab Т 2 s - J
> min.
Тогда в точке экстремума
' f ( a , Ь ) d a
' ff ( a , b ) d b
S Vi
= S V i
—
—
|
as i ab |
s i b |
|
2 b " 2 s i |
— 2 b 2 s i |
|
as i ab |
[ as i a - |
|
2 b " 2 s " _ |
[_ 2 b 2 2s ; J |
= 0.
= 0,
После преобразований получим
<
( 1v l—yS Visi
V 2 i
an b2 + 2
■ ab 2 = 0,
2 S ys
—-E s2
4 S '
Окончательно для определения неизвестных коэффициентов a и b получим следующую систему нелинейных уравнений:
-
ai a a
-
-1 + a2 b + + a4 a + a5 a b 2 = 0,
< (7)
в а R a -l вз а R a^h n
"b^T + в2 a + b“ + в4ab = 0, где коэффициенты αn и βn определяются согласно (6), n — количество измерений.
Эта система может быть решена численно, например в приложении MathCAD, что и было проделано в настоящей работе.
С практической точки зрения интересно изучить поведение полученного алгоритма в условиях вносимых погрешностей измерений при определении величин скольжения и вращающего момента.
В этой связи после успешного тестирования алгоритма при точных значениях величин si и Mi эти величины брались с отклонением в 3 % от их истинных значений. Испытания проводились с различным количеством измерений (от 7 до 50), а также с различными интервалами по шкале величин скольжений ( s < 0,5 sKp , s < 0,6 s р , s < 0,7 sp ).
На рис. 2, 3 представлены результаты этих исследований для величин математических ожиданий M и среднеквадратичных отклонений σ ошибок определения искомых величин sкр и
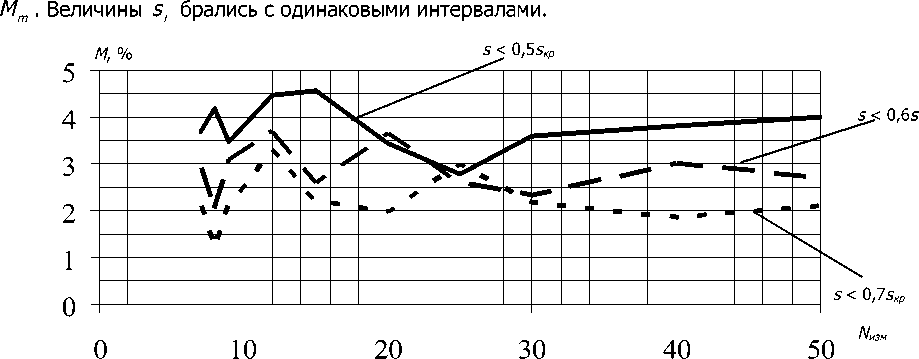
Рис. 2. Зависимости математического ожидания (в процентах) ошибки измерения от количества измерений на различных
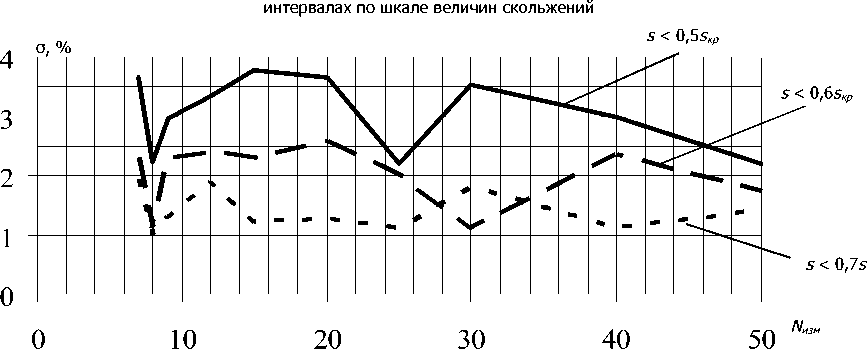
Рис. 3. Зависимости среднеквадратичного отклонения (в процентах) ошибки измерения от количества измерений на различных интервалах по шкале величин скольжений
Данные рис. 2, 3 иллюстрируют рост устойчивости в определении искомых величин при увеличении объёма выборки и ширины участка по шкале величин скольжений. Начиная с объёма выборки, равного 40, устанавливаются удовлетворительные (не превышающие значения вносимой погрешности) значения величин M и о. Однако для кривой, соответствующей s < 0,5 sKp , эти значения недопустимо велики, поэтому целесообразно применять интервалы измерений s < 0,6 sp или s < 0,7 sp .
Поскольку устойчивость расчётов определяется в том числе величиной интервала по оси скольжений, то представляется желательным получить возможность определения этого интервала каким-либо алгоритмическим способом.
На рис. 4 представлены нормированные (к величине максимального момента) зависимости m ( s ), а также её первая и вторая производные m '( s ) и m "( s ) соответственно. Видно, что функция m "( s ) имеет минимум в интересующей нас области, который можно использовать для опре-
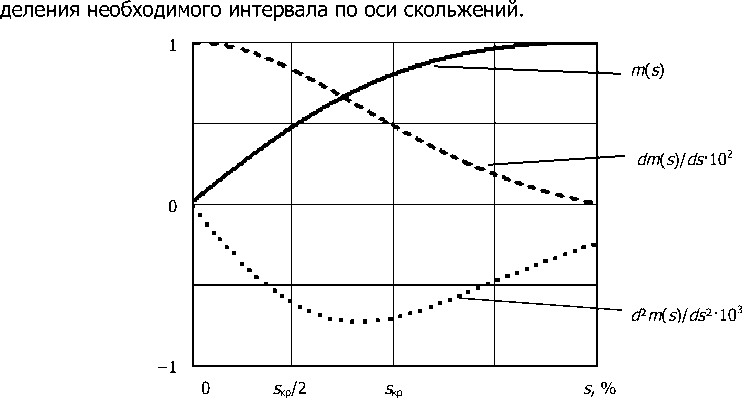
Рис. 4. Зависимости нормированных функций момент-скольжение, а также её первой и второй производной
от скольжения
Для нормированной функции момент-скольжение m ( s ) =
M (s)
m (si)
si +r s1
.
Трижды дифференцируя (8), получим:
m ”( s 1 ) =
— 12
1 1 4
• +
-
I 2 I
-
V s 1 )
•
I s 1 + s i J
Решая уравнение m '"( s 1 ) = 0, получим:
113 I s13 si M s1)
—
1 1
J + s i )
1 1 4
s 1 + _ I s 1
s 1 )
.
-
— 12 s — 6 s - +1 = 0. ( s* + 1 ) 4
-
3. Результаты и выводы. Данный метод может быть положен в основу диагностического устройства, работающего на базе микропроцессора. Для диагностики можно использовать и ПК, считывающий информацию непосредственно с измерительных датчиков. При этом, если отсутствуют какие-либо данные о величинах sкр и Mm , то для их поиска исследуемый двигатель должен сделать два прогона. Первый — для приближённого определения величины интервала по оси скольжений. Для этого нужно найти s min , что позволит определить величину шага si . На втором прогоне будут найдены параметры sкр и Mm .
Отсюда s14 - 6s12 +1 = 0 .
Это уравнение имеет корни:
s1‘=(-2,414 -0,414 0,414 2,414), из которых условию задачи удовлетворяет s*3 = 0,414, то есть smin = 0,414 ■ дкр .
Значит, отследив равенство нулю третьей производной функции m ( s ) , можно с некоторой точностью «масштабировать» ось скольжений, определив таким образом необходимый для измерения интервал. Учитывая, что погрешность численного дифференцирования растёт с ростом степени производной, в данном случае лучше следить за функцией m "( s ) , определив величину s min как аргумент, при котором эта функция имеет минимальное значение.
Для реализации этого метода использовались общие математические подходы. Поэтому сфера его применения не исчерпывается решением представленной здесь задачи. Так, например, модифицируя регрессионную функцию, с его помощью можно экспериментально определить параметры однофазного трансформатора P 0 и Pк , задавшись известной в электротехнике формулой для зависимости КПД от коэффициента загрузки [4]:
β Sн cosφ
-
в S h cosф + P 0 + в Р '
Список литературы Применение математической регрессии для определения параметров трёхфазного асинхронного двигателя
- Способ диагностики электродвигателя переменного тока и связанных с ним механических устройств: патент RU 2339049 С1 Рос. Федерация/В. С. Петухов. -№ 2007107715/28; заявл. 02.03.2007; опубл. 20.11.2008, Бюл. № 32.
- Комплексный метод диагностики асинхронных электродвигателей на основе использования искусственных нейронных сетей [Электрон. ресурс]/ООО «Олбест». -Режим доступа: http://knowledge.allbest.ru/transport/2c0a65625a3ac78b4d53a88521216c27_0.html (дата обращения: 10.04.13).
- Чернов, Д. В. Функциональная диагностика асинхронных двигателей в переходных режимах работы: дис.. канд. техн. наук/Д. В. Чернов. -Ульяновск, 2005. -129 с.
- Пантюшин, В. С. Общая электротехника/В. С. Пантюшин. -Москва: Высш. школа, 1970. -568 с.
- Гмурман, В. Е. Теория вероятностей и математическая статистика/В. Е. Гмурман. -Москва: Высш. образование, 2006. -479 с.


