Применение медианных фильтров с взвешенным центральным элементом для очистки изображений от импульсного шума

В процессе передачи и преобразования посредством радиотехнических систем изображения подвергаются воздействию различных помех, что в ряде случаев приводит к ухудшению визуального качества и потере участков изображений. С широким внедрением цифровых систем связи увеличивается актуальность решения задач восстановления изображений, полученных с по- мощью фото- и видеокамер, с целью фильтрации изображений. На практике часто встречаются изображения, искаженные шумом, который появляется на этапах формирования и передачи его по каналу связи [1]. Линейные алгоритмы фильтрации применяются для реставрации и улучшения визуального качества изображений. Их можно применять для снижения уровня шума на изображениях. Однако, чтобы подавить шум и при этом сохранить контурную часть изображений, приходится применять нелинейные фильтры [2].

Все линейные алгоритмы фильтрации приводят к сглаживанию резких перепадов яркости изображений, прошедших обработку. Недостаток в том, что линейные процедуры являются оптимальными при гауссовском распределении сигналов, помех и наблюдаемых данных. Реальные изображения не подчиняются данному распределению вероятностей. Одна из основных причин этого состоит в наличии у изображений разнообразных границ, перепадов яркости, переходов от одной текстуры к другой. Поддаваясь локальному гауссовскому описанию в пределах ограниченных участков, многие реальные изображения в этой связи плохо представляются как глобально гауссовские объекты. Именно это и служит причиной плохой передачи границ при линейной фильтрации. Вторая особенность линейной фильтрации – ее оптимальность, как только что упоминалось, при гауссовском характере помех. Обычно этому условию отвечают шумовые помехи на изображениях, поэтому при их подавлении линейные алгоритмы имеют высокие показатели.

Однако часто приходится иметь дело с изображениями, искаженными помехами других типов. Одной из них является импульсный шум. При ее воздействии на изображении наблюдаются белые и черные точки, хаотически разбросанные по кадру [3]. Применение линейной фильтрации в этом случае неэффективно – так как каждый из входных импульсов дает отклик в виде импульсной характеристики фильтра, а их совокупность способствует распространению помехи на всю площадь кадра.

Удачным решением перечисленных проблем является применение медианной фильтрации, разработанной в [4]. Медианная фильтрация применяется в обработке инфракрасных изображений [5], изображений, сделанных под водой [6], а также в медицине: при очистке рентгеновских снимков от шума [7], снимков, полученных с помощью магнитно-резонансной томографии [8] и снимков сетчатки глаза [9]. Кроме того, медианные фильтры (МФ) находят применение в системах адаптивной фильтрации изображений [10].

Медианный фильтр может быть спроектирован так, чтобы наилучшим образом удалить шум, но МФ с взвешенным центральным элементом (ВЦЭ) дает аналогичные результаты, и путем выбора веса центрального элемента фильтра пользователь может получить желаемый уровень сглаживания [11].

Поскольку центральный вес уменьшается для достижения желаемого уровня подавления импульса, выходное изображение будет испытывать повышенные искажения, особенно вокруг мелких деталей изображения. Тем не менее применение МФ с ВЦЭ может быть очень эффективным в устранении шума «соль и перец», сохраняя при этом детали изображения [12].

В этой статье мы покажем зависимость качества восстановления изображения, искаженного импульсным шумом, от его интенсивности и веса МФ с ВЦЭ.

Будем считать, что цифровые изображения представляются набором чисел на квадратной решетке {.Yy j } ’ где и,й изменяются по z² или по некоторому подмножеству Z², где z – это множество целых чисел.

Рассмотрим простой МФ, в котором фильтрация осуществляется посредством движения окна некоторой маски вдоль последовательности дискретных отсчетов и замены значения в центре маски медианой исходных отсчетов внутри маски. Обозначим как W<)} И {У(у)} входной и выходной компоненты МФ соответственно, тогда

Жй =

4            .X 7 2     (1)

= median{X(i-s,j-Й | (s,0 e PT,(i,j) e Z"), где W – «окно» (далее без кавычек), которое определяется в окрестности начала координат. Например, для (2L + l)x(2Z + l) квадратное окно задается как W = sv(sA\-L

Рассмотрим простой МФ с весами

< h(s, ^) | (5, t) g W, ^^h(s,t)-c >, _                        Vs,iW            ,

где c – нечетное целое, большее или равное размеру окна. При получении выходных данных У(/, /) данный МФ генерирует h(s,t) копии ХЦ-sJ-t) для каждого (s,t)eW, всего c выборок значений. Затем берется медианное значение c -выборок. Таким образом, Y(i,j) представляется в виде

ЖЛ =

= median{h(s,t)OX(i — s,j — 0 | ($,0 e Wy (3)

При применении МФ происходит последовательная обработка каждой точки кадра, в результате чего образуется последовательность оценок. В принципе, для каждого отсчета выполняется независимая оценка медианы в окне. В целях ускорения оценки целесообразно алгоритмически на каждом шаге использовать ранее выполненные вычисления. Отсчеты изображения, оказавшиеся в пределах окна, образуют рабочую выборку текущего отсчета.

Чтобы выполнить данную фильтрацию для элемента изображения, необходимо сначала упорядочить по возрастанию значения пикселей внутри окрестности, затем найти значение медианы и, наконец, присвоить полученное значение обрабатываемому элементу. Так, для окрестности 3x3 элементов медианой будет пято е значение по величине, для окрестности 5x5 – тринадцатое значение, и так далее [13].

Например, пусть в окрестности 3x3 элементы имеют следующие значения: {90,150, 83,163, 255,132,72,142,173}, где элемент 255 соответствует центру окна. Большое значение ярко сти в этой точке кадра является результатом воздействия импульсного шума. Упорядоченная по убыванию выборка имеет вид: {72, 83, 90,132,142,150,163,173, 255}, следовательно в соответствии с процедурой на выходе МФ получаем значение 142.

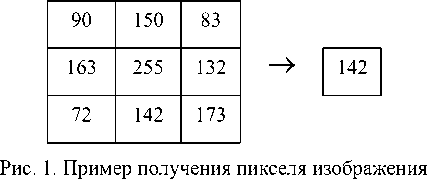
после применения медианного фильтра с окном 3x3

Простой МФ с центральным весом //(0,0) = 2^ + 1 и h{s,t) = 1 для каждого (^,0*(0,0) называется МФ с взвешенным центральным элементом (ВЦЭ), где к - неотрицательное целое число. Выход Y(i,j) МФ с ВЦЭ задается выражением

Y (i, 7) = median ^X (i — s,j — ty 2K0X(i,j)\(S,t)eWy

где вертикальный «ромбик» означает, что в массиве, который необходимо отсортировать, необ- ходимо использовать элемент ху, й не один раз, а взять его 2K копий [12]. Если K=0, то МФ с ВЦЭ становится простым медианным фильтром, а когда 2^ + 1 больше или равен размеру окна 2£ + l, он становится тождественным фильтром, не изменяющим сигнал.

Утверждение [11]. Для независимых и одинаково распределенных входов функция распределения выходного сигнала F_Y МФ с ВЦЭ с размером 2£ + l и центральным весом 2 K + 1 задается выражением

2/.

FY=^CyFry-FxfL-J +

2L                                        (5)

^CyF^-FxyL+'"J , где kv=L + ;-K , k,=L + l + K ,FX – входное распределение и c* = – биномиальные коэффициенты. Далее мы рассмотрим подавление шума при помощи МФ с ВЦЭ с масками 3x3, 5x5 и 7x7.

Под импульсным шумом понимаем искажение сигнала импульсами, то есть выбросами с очень большими положительными или отрицательными значениями и малой длительностью. При обработке изображений импульсный шум возникает, например, вследствие ошибок декодирования, которые приводят к появлению черных и белых точек на изображении. Поэтому его часто называют точечным шумом. Выбросы шума особенно заметны на очень темных или очень светлых участках изображений. Для таких участков можно вывести формулы для вероятности правильного воспроизведения [14].

Появление выброса шума в каждой точке (6 j) изображения имеет вероятность p и не зависит ни от наличия шума в других точках изображения, ни от исходного изображения. Искаженная точка приобретает стабильное значение d , соответствующее черному или белому цвету. Пусть ^sxX – искаженное изображение. Тогда

^S(i,j) с вероятностью (1-/?);

^(б7) =                              (6)

{« с вероятностью р, где №7)}" значения неискаженного изображения. Пусть N равно максимально возможному значению пикселя изображения: например, для 8-битных изображений в оттенках серого N = 255. При допущении о том, что при импульсном шуме появление белых или черных пикселей равновероятно, модель импульсного шума может быть переписана в виде:

Рг{ЖУ) = 0} = , Рг{Жу) -N^^-,

(7) рг№п-8а,п^\-р.

где Рг{Л} – вероятность появления события Л.

При рассмотрении МФ с размером окна 2L + 1 и весом центрального элемента 2^ + 1 поиск медианы при вычислении результата работы фильтра осуществляется по массиву, состоящему из 2L + 2K + 1 элементов.

Если центральный пиксель части изображения, к которой применен МФ с ВЦЭ, имеет минимально возможное значение 0, то для того, чтобы результатом работы фильтра был 0, необходимо и достаточно, чтобы среди оставшихся 2L пикселей части изображения не менее (2L-2K-1V2 пикселей имели значения 0. Поскольку количество пикселей является целым числом, то это требование можно заменить на требование равенства 0 не менее L-K пикселей части изображения.

Если центральный пиксель части изображения, к которой применен МФ с ВЦЭ, имеет значение, отличное от 0, то для того, чтобы результатом работы фильтра был 0, необходимо и достаточно, чтобы среди оставшихся 2L пикселей части изображения не менее (2£ + 2^ + 1)/2 пикселей имели значения 0. Поскольку количество пикселей является целым числом, то это требование можно заменить на требование равенства 0 не менее £ + ^ + 1 пикселей части изображения.

Таким образом, вероятность получения 0 в качестве результата работы МФ с ВЦЭ равна

2L / \V рк№п=т=^ q[Wi-^ + i=L-K \ ^ У \      7

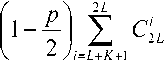
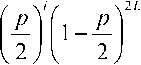
С учетом (8)-(9) можно найти вероятности получения «искаженного» результата работы МФ с ВЦЭ, соответствующего получению 0 или N на выходе фильтра, и «неискаженного» результата работы МФ с ВЦЭ, соответствующего получению значений, отличных от 0 или N на выходе фильтра:

Рг{У(/, У) -«искажен»} =

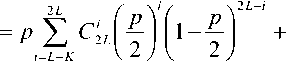
+ (2-/?) ^ c;/^Ki-^ i=L+K+\ V V .

Рг{У(/,У) — «не искажен»} =

-\-p^Lc\l i=L-K

-(2-р) У C}J^ 1-^

i=L+K+1 V \      .

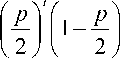
В таблицах 1-3 приведены значения вероятностей получения неискаженных пикселей изображения, рассчитанные по формуле (11) для медианных фильтров с размерами масок 3x3, 5x5 и 7х7, с различными весами центральных элементов для значений вероятности р = 0,01; 0,05; ОД; 0,25; 0,5.

Из таблиц 1-3 видно, что во всех случаях вероятность получения неискаженного пикселя изображения уменьшается с ростом коэффициента К.

p/f№V) = o) = y £ c;/yKi-y) + i=L-K V 7 V ^7

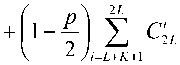
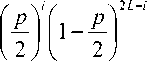
С учетом допущения равной вероятности появления черных и белых пикселей при импульсном шуме можно записать аналогичную формулу для вероятности получения N в качестве результата работы МФ с ВЦЭ:

Для оценки структурного изменения изображения после применения МФ с ВЦЭ предположим, что пиксели изображения подчиняются равномерному закону распределения с функцией распределения

Fx^ =

О,

если л- < 0;

—, если 0 <  х < N; N

если х >

где А" – уровень яркости пикселя изображения.

Таблица 1. Вероятность получения неискаженного пикселя изображения, искаженного импульсным шумом с вероятностью р , и восстановленного МФ 3x3 С L = 4 и весом центрального элемента 2ЛГ + 1 .

К	Вероятность, p
	0,01	0,05	0,1	0,25	0,5
0	1,000000	0,999998	0,999934	0,995035	0,902145
1	1,000000	0,999960	0,999420	0,983014	0,832932
2	0,999993	0,999209	0,994276	0,934070	0,682968
3	0,999607	0,990833	0,966342	0,835902	0,550034
4	0,990000	0,950000	0,900000	0,750000	0,500000

Таблица 2. Вероятность получения неискаженного пикселя изображения, искаженного импульсным шумом с вероятностью р , и восстановленного МФ 5x5 с L =12 и весом центрального элемента 2^ + 1

К	Вероятность, p
	0,01	0,05	0,1	0,25	0,5
0	1,000000	1,000000	1,000000	0,999996	0,993259
1	1,000000	1,000000	1,000000	0,999985	0,988546
2	1,000000	1,000000	1,000000	0,999914	0,972500
3	1,000000	1,000000	1,000000	0,999586	0,939311
4	1,000000	1,000000	0,999999	0,998292	0,883097
5	1,000000	1,000000	0,999987	0,994030	0,803706
6	1,000000	0,999999	0,999904	0,982426	0,711078
7	1,000000	0,999986	0,999403	0,956777	0,623324
8	1,000000	0,999861	0,997022	0,911891	0,557509
9	0,999998	0,998932	0,988406	0,852043	0,519901
10	0,999936	0,993990	0,966082	0,794916	0,504515
11	0,998867	0,977232	0,929199	0,760142	0,500502
12	0,990000	0,950000	0,900000	0,750000	0,500000

Таблица 3. Вероятность получения неискаженного пикселя изображения, искаженного импульсным шумом с вероятностью р, и восстановленного МФ 7x7 с Z = 24 и весом центрального элемента 2^ + 1

К	Вероятность, p
	0,01	0,05	0,1	0,25	0,5
0	1,000000	1,000000	1,000000	1,000000	0,999839
1	1,000000	1,000000	1,000000	1,000000	0,999729
2	1,000000	1,000000	1,000000	1,000000	0,999306
3	1,000000	1,000000	1,000000	1,000000	0,998237
4	1,000000	1,000000	1,000000	1,000000	0,995 822
5	1,000000	1,000000	1,000000	0,999999	0,990823
6	1,000000	1,000000	1,000000	0,999998	0,981325
7	1,000000	1,000000	1,000000	0,999990	0,964780
8	1,000000	1,000000	1,000000	0,999962	0,938411
9	1,000000	1,000000	1,000000	0,999867	0,900057
10	1,000000	1,000000	1,000000	0,999575	0,849294
11	1,000000	1,000000	1,000000	0,998756	0,788378
12	1,000000	1,000000	1,000000	0,996685	0,7223 86
13	1,000000	1,000000	0,999998	0,991983	0,658177
14	1,000000	1,000000	0,999989	0,982455	0,602417
15	1,000000	1,000000	0,999945	0,965355	0,559525
16	1,000000	0,999999	0,999755	0,93 8422	0,530572
17	1,000000	0,999991	0,999053	0,901635	0,513624
18	1,000000	0,999939	0,996829	0,858718	0,505151
19	1,000000	0,999658	0,990933	0,816798	0,501603
20	0,999999	0,998410	0,978204	0,783453	0,5003 94
21	0,999982	0,994086	0,956705	0,762705	0,500072
22	0,999758	0,983086	0,930065	0,753233	0,500009
23	0,997862	0,964832	0,908526	0,750411	0,500001
24	0,990000	0,950000	0,900000	0,750000	0,500000

Тогда функция распределения пикселей изображения, искаженного импульсным шумом, по формуле (6) будет иметь вид

О,

если х < 0;

Р , ^~Р)х 2 N

если 0 < х <  N; (13)

если х >  N.

График функции (13) на промежутке (o,n) для р = ОД и N = 255 (случай 8-битных изображений в оттенках серого) показан на рис. 2а. Результат применения МФ с ВЦЭ искажает обрабатываемое изображение. Для оценки уровня этого искажения необходимо исследовать функцию в F_Y (X) из формулы (5) с учетом подстановки в нее функции F_x^ из формулы (13).

На рис. 2 б - 2 е показан график функций F^xY полученный для случая р = 0,1, N = 255, L = 4

(случай МФ 3x3) с различными значениями K = 0;l;2;3;4 .

Из рис. 2 б - 2 е видно, что для малых значений К функция распределения Fy ^х^ существенно изменяется относительно функции F^xY а при увеличении К разница между этими функциями становится все меньше и меньше. Для оценки степени различия функции F_y (х) и F_x^ будем использовать величину I:

N

I = J|F_y (x) - F_Y (x)|t7x.

Геометрический смысл этого интеграла показан на рис. 3: он равен площади фигуры, заключенной между графиками функции F_y(x) и F_x(x). Чем меньше величина I, тем ближе функции F_y (x) и F_Y (л) друг к другу в смысле метрики функционального пространства.

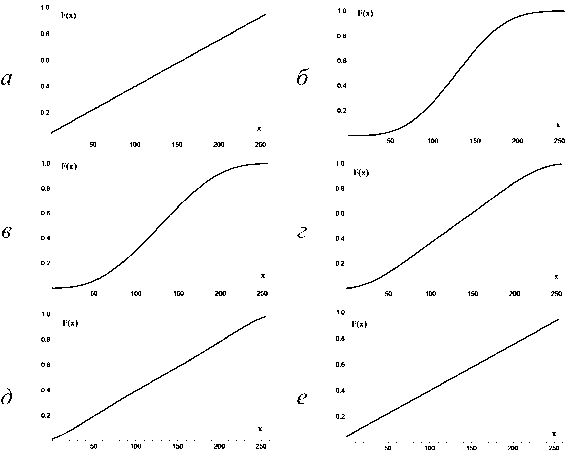
Рис . 2. Графики функций распределения для изображений в оттенках серого с N = 255, обработанных МФ с Z = 4 и различными весовыми коэффициентами центрального элемента: a ) зашумленное изображение /2 = 0,1; б ) ^ = 0;

в ) ^ = 1 ; г ) ^ = 2 ; д ) ^ = 3 ; е ) K = 4

В таблицах 4-6 приведены значения величины I из формулы (14) для изображений в оттенках серого с # = 255, зашумленных импульсным шумом с вероятностями /> = 0.01; 0,05; 0,1; 0,25; 0,5, и медианных фильтров с масками 3x3, 5x5, 7x7 с различными весами центрального коэффициента.

Из таблиц 4 - 6 видно, что увеличение веса центрального элемента К ведет к уменьшению величины I во всех случаях. Это означает, что применение больших коэффициентов центрального элемента в МФ с ВЦЭ значительно меньше искажает структуру изображения по сравнению с малыми значениями К .

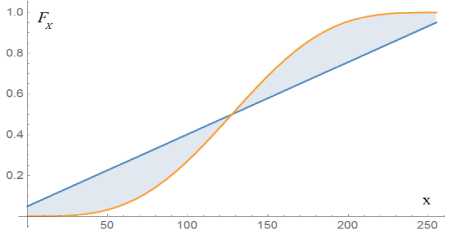
Рис. 3. Геометрический смысл величины 1 для случая N = 255, р = ОД, L = 4, K = 0

Как было показано ранее, увеличение коэффициента к , с одной стороны, уменьшает структурное искажение изображения от применения МФ, а с другой стороны увеличивает вероятность получения искаженных значений пикселей, то есть вероятность пропуска шумовых компонент. Таким образом, практическое применение МФ требует нахождения оптимальной величины к, которая позволяла бы минимально искажать структуру обрабатываемого изображения при максимально большой вероятности корректной очистки от шума.

Таблица 4. Значения величины 1 для МФ 3x3 с L = 4 и весом центрального элемента 2 К + 1 (случаи N = 255 )

К	Вероятность, р
	0,01	0,05	0,1	0,25	0,5
0	32,6936	33,9091	35,2619	37,8891	35,2864
1	27,0591	28,0375	29,0655	30,5709	26,7776
2	15,7902	16,2954	16,6891	16,3175	11,9662
3	5,5946	5,6899	5,6186	4,6649	2,5224
4	0	0	0	0	0

Таблица 5. Значения величины I для МФ 5x5 с £ = 12 и весом центрального элемента 2ЛГ + 1 (случай N = 255 )

К	Вероятность, р
	0,01	0,05	0,1	0,25	0,5
0	44,4278	46,1374	48,1694	53,3407	56,1843
1	42,9539	44,6014	46,5480	51,3952	53,3352
2	39,0935	40,5785	42,3016	46,2998	45,9520
3	33,7593	35,0197	36,4339	39,2601	36,0178
4	27,8293	28,8400	29,9109	31,4394	25,5593
5	21,9678	22,7317	23,4633	23,7285	16,2189
6	16,5806	17,1177	17,5376	16,7021	9,0108
7	11,8699	12,2086	12,3570	10,7121	4,2463
8	7,9171	8,0895	8,01543	6,0025	1,6206
9	4,7486	4,7890	4,55979	2,7354	0,4667
10	2,3712	2,3208	2,04596	0,8906	0,0896
И	0,7866	0,7127	0,54411	0,1532	0,0086
12	0	0	0	0	0

Таблица 6. Значения величины I для МФ 7x7 с L = 24 и весом центрального элемента 2К + 1 (случай N = 255 )

К	Вероятность, р
	0,01	0,05	0,1	0,25	0,5
0	49,9278	51,8690	54,2194	60,6007	66,9959
1	49,3612	51,2786	53,5961	59,8528	65,8749
2	47,7741	49,6246	51,8502	57,7578	62,7357

Таблица 6. Значения величины I для МФ 7х7с£ = 24и весом центрального элемента 2 К +1 (случай N = 255 ) (окончание)

К	Вероятность, р
	0,01	0,05	0,1	0,25	0,5
3	45,3681	47,1173	49,2037	54,5819	57,9812
4	42,3754	43,9986	45,9117	50,6315	52,0785
5	39,0222	40,5042	42,2232	46,2053	45,4914
6	35,5023	36,8361	38,3513	41,5590	38,6320
7	31,9632	33,1479	34,4582	36,8874	31,8398
8	28,5060	29,5452	30,6554	32,3241	25,3848
9	25,1934	26,0931	27,0115	27,9517	19,4807
10	22,0602	22,8280	23,5650	23,8170	14,2955
11	19,1242	19,7683	20,3353	19,9447	9,9504
12	16,3933	16,9224	17,3313	16,3493	6,5076
13	13,8708	14,2938	14,5567	13,0437	3,9563
14	11,5581	11,8837	12,0127	10,0467	2,2091
15	9,4555	9,6926	9,6999	7,3880	1,11757
16	7,5631	7,7205	7,6186	5,1096	0,5043
17	5,8810	5,9676	5,7697	3,2581	0,1992
18	4,4091	4,4338	4,1558	1,8660	0,0673
19	3,1475	3,1194	2,7844	0,9273	0,0189
20	2,0962	2,0255	1,6716	0,3812	0,0042
21	1,2552	1,1561	0,8423	0,1208	0,0007
22	0,6244	0,5226	0,3147	0,0260	0,0000
23	0,2048	0,1410	0,0646	0,0029	0,0000
24	0	0	0	0	0

Для моделирования были использованы полутоновые изображения «горы» и «грибы», которые изображены на рис. 4 и рис. 5 вместе с зашумленными импульсным шумом изображениями, сгенерированными функцией imnoise в программ- ной среде Matlab R2015b.

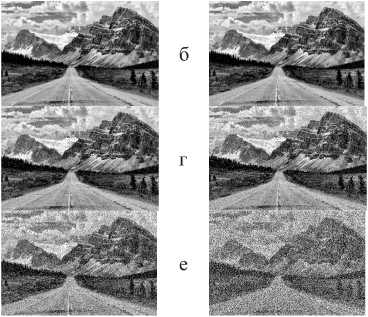
Рис . 4. Изображение «горы», зашумленные импульсным шумом с различной интенсивностью: а) исходное изображение; б) р = 0,01; PSNR = 24,9554;

^р = 0,05 ; PSNR= 18,012; г) р = 0,1; PSNR= 15,0178;

д) р = 0,25; PSNR = 11,0529; с) р = 0,5 ; PSNR = 8,0322

В качестве вероятности появления шумовых пикселей были выбраны значения р = 0,01;0,05;0,1;0,25;0,5.

Для оценки качества очистки изображения от шума была использована характеристика PSNR (пиковое отношение «сигнал-шум»), которая вычисляется по формуле:

P5W = 101og10

гр Л

MSE ,

где MSE = ---- — -----—-— – среднеквадра-

^1 ^2

тическая ошибка сравнения качества восстановленного изображения; N – максимальная величина пикселя изображения; D^ и D₂ – ширина и высота изображения, а суммирование производится по всем координатам пикселей изображения.

Величина PSNR имеет логарифмическую природу, и единицей ее измерения является дБ. Чем больше величина PSNR, тем лучше качество восстановленного изображения, для тождествен- но равных изображений PSNR = oo . При иссле- довании алгоритмов сжатия и очистки от шума изображений в оттенках серого практически пригодной считается величина PSNR, изменяющаяся в пределах от 20 дБ до 50 дБ.

Рис. 5. Изображение «грибы», зашумленные импульсным шумом с различной интенсивностью: а) исходное изображение; б) /> = 0,01, PSNR=24,6028; в) p = 0,05 ; PSNR = 17,6645; r) p = 0,1; PSNR = 14,649; д) p = 0,25; PSNR = 10,6848; e) p = 0,5; PSNR = 7,6496

Над зашумленными изображениями на рис . 4 - 5 были применены МФ с ВЦЭ с окнами W размером 3x3;5x5 и 7x7, которым соответствуют значения L = 4; Z = 12 и Л = 24. Для каждого медианного фильтра были испытаны все возможные значения веса центрального элемента К : 0 <  К < L. На рисунке 6 показан пример обработки изображения «горы» с уровнем шума р = 0,25 при помощи МФ с ВЦЭ с окном W размером 3x3 и различными К . Результаты обработки изображений «горы» и «грибы» во всех случаях показаны на рис. 7 - 8.

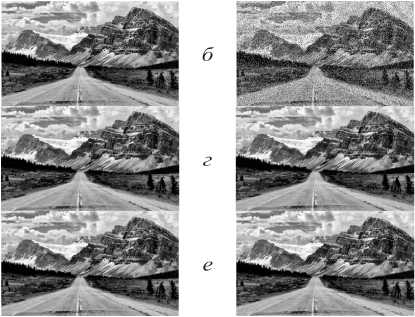
Рис. 6. Результат обработки изображения «горы», зашумленного импульсным шумом с р = 0,25 МФ с окном 3x3 с различными весами центрального элемента: а ) исходное изображение; б ) зашумленное изображение, PSNR = 11,0529; в ) к = о , PSNR= 23,9900; г ) ^ = 1, PSNR = 21,3842; д ) ^ = 2 , PSNR = 16,4518; е ) К = 3 , PSNR = 12,7548

На рис. 7 а , 7 б , 8 а и 8 б отчетливо видно возрастание качества очистки от шума, выраженного величиной PSNR, достижение максимального значения и последующее снижение качества обработки, при изменении К от 0 до L , во всех случаях. Это связано с тем, что для небольших уровней шума существенную роль играет сохранение структуры изображения, изменения которой зависит от величины I , приведенной в таблицах 4 - 6. Снижение качества обработки для больших значений К объясняется существенным снижением вероятности получения неискаженного пикселя изображения, которая приведена в таблицах 1-3.

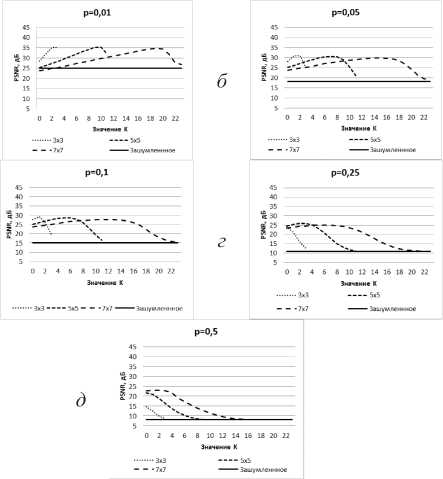
Рис. 7. Результаты обработки МФ изображения «горы» с различными уровнями импульсного шума: а) р = 0,01; б) р = 0,05 ; в) р = 0,1; г) р = 0,25; д) р = 0,5

Для высоких уровней шума (см. рис.7 в - 7 д , 8 в - 8 д ) возрастание качества обработки до достижения максимального значения за счет уменьшения величины I уже не так хорошо заметно из-за существенного увеличения влияния вероятности получения неискаженного пикселя изображения. Наилучшие значения PSNR между исходными изображениями и изображениями, очищенными от шума при помощи МФ с ВЦЭ, приведены в таблице 8. Из таблицы 8 видно, что для уровней шума от 0,01 до 0,1 наилучший результат показывает фильтр с окном 3x3.

Для уровня шума р = 0,25 наилучший результат показывает фильтр с окном 5x5, а для уровня шума Р = 0,5 наилучший результат показывает фильтр с окном 7x7. Данный факт может быть объяснен тем обстоятельствам, что наилучшие результаты обработки изображений достигались при к*о.

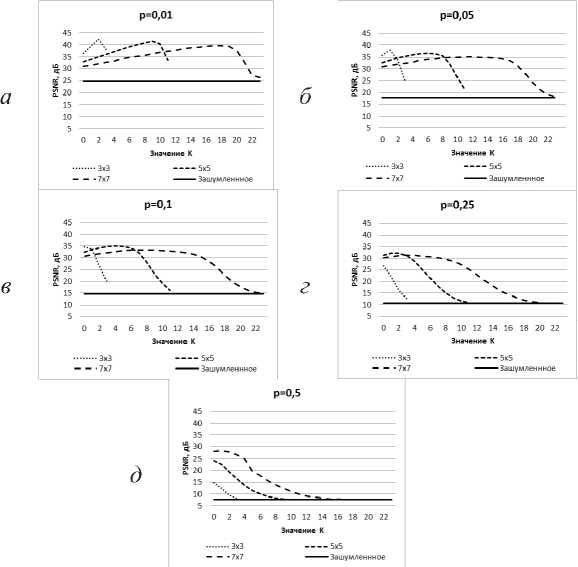
Рис. 8. Результаты обработки МФ изображения «грибы» с различными уровнями импульсного шума: а ) 72 = 0,01;

б ) р = 0,05 ; в) Р = 0,1 ; г) /> = 0,25 ; д) р = 0,5

В тех случаях, когда ^ = 0, результат не являлся наилучшим по причине строгого убывания величины PSNR (это хорошо видно на графиках из рис. 7 - 8). Другими словами, значения PSNR не является экстремальным для этих случаев, что и объясняет относительно низкий результат обработки. Улучшение результата обработки изображений с высоким уровнем шума фильтрами большего размера объясняется относительно высокой вероятностью получения неискаженных пикселей изображения. Это хорошо видно из верхних строк таблиц 1-3. Так, например, для уровня шума Р = 0,5 вероятность получения неискаженного пикселя изображения, обработанного фильтром 3x3 с^ = 0 , составляет «0,9021; обработанного фильтром 5x5 с^ = 0 составляет «0,9933; обработанного фильтром 7x7 с^ = 0 составляет «0,9998.

Полученные результаты могут быть систематизированы следующим образом: для небольших уровней шума лучшее качество обработки изображений в оттенках серого достигается при использовании медианных фильтров наименьшего размера (3x3). Для высоких уровней шума целесообразнее использовать медианные фильтры большего размера (5x5 и 7x7). Для использования МФ с ВЦЭ на практике следует определять характеристики возникающего шума для подбора наилучшего размера маски фильтра и веса центрального элемента. Кроме того, МФ с ВЦЭ могут быть использованы в системах адаптивной фильтрации изображений следующим образом: осуществлять определение уровня шума с последующим подбором наилучшего МФ с ВЦЭ по показателю уровня очистки.

Таблица 8. Наилучшие значения PSNR при МФ изображений с различными уровнями интенсивности импульсного шума

Уровни интенсивности шума, р	Размер окна	Изображение «горы»		Изображение «грибы»
		PSNR, дБ	К	PSNR, дБ	к
0,01	3x3	35,5095	3	42,2584	2
	5x5	35,4846	10	41,4250	9
	7x7	34,7326	19	39,6269	18
0,05	3x3	30,9645	2	37,8918	1
	5x5	30,6255	7	36,6489	6
	7x7	29,7289	15	35,0498	12
0,1	3x3	29,2184	1	34,6385	0
	5x5	28,5595	5	34,9324	4
	7x7	27,6093	12	33,2754	8
0,25	3x3	23,9896	0	26,7474	0
	5x5	25,8744	3	32,2554	2
	7x7	25,0730	4	31,3112	4
0,5	3x3	14,6351	0	14,6638	0
	5x5	21,5800	0	24,1330	0
	7x7	22,9915	2	28,4957	1

В работе показано применение МФ с взвешенными центральными элементами для очистки от импульсного шума изображений в оттенках серого. Показано, что на качество обработки влияют две характеристики: вероятность получения неискаженного пикселя изображения и уровень искажения функции распределения пикселей изображения. Фильтры с окном 3x3 в меньшей мере искажают входное изображение, однако имеют меньшую вероятность получения неискаженного пикселя изображения. Данные фильтры позволяют получать более высокое качество очистки изображений от шума с небольшой вероятностью искажения пикселей (р<0,1).

Медианные фильтры с размерами окон 5x5 и 7x7 значительно сильнее искажают функцию распределения пикселей изображения, однако имеют значительно более высокую вероятность получения неискаженных пикселей при обработке. Такие фильтры позволяют получать более высокое качество очистки изображений от шума с высокой вероятностью искажения пикселей (^>0,1). Причем чем выше уровень шума, тем больший размер маски МФ может потребоваться.

Полученный результат может быть использован для улучшения качества медицинских и спутниковых изображений, а также при разработке систем адаптивной фильтрации. При этом для эффективного практического использования необходимо проводить технический анализ системы на шумовые характеристики для подбора наилучшего соотношения размера маски МФ и веса его центрального элемента. Работа выполнена при финансовой поддержке гранта Президента Российской Федерации МК-5980.2016.9.

Chervyakov N.I., Lyakhov P.A., Orazaev A.R.

North-Caucasus Federal University, Stavropol, Russian Federation