Применение метода автокорреляционного анализа в исследовании многолетней динамики численности жужелиц (Coleoptera, Carabidae) Баргузинского хребта

Многолетние наблюдения за динамикой численности живых организмов, дающие возможность получения статистически достоверных результатов анализа, позволяют взглянуть на экосистемные процессы по-новому. Исследование ритмики природных процессов входит в задачу экологического мониторинга и является важным направлением научно-исследовательской деятельности заповедников [1]. Изучение временных рядов позволяет приблизиться к пониманию их внутренней природы [2]. При помощи некоторых статистических процедур могут быть решены задачи, которые не поддаются изучению традиционными способами обработки биологических данных [3].

Жуки-жужелицы являются наиболее крупной таксономической группой герпетобионтных насекомых, на долю которой приходится до 70% количественного состава среди остальных групп в Баргузинском заповеднике. Многолетние учеты численности жужелиц позволили провести более детальный анализ данных [4]. Предметом нашего внимания в предлагаемой статье было обнаружение периодической компоненты в многолетних рядах численности жужелиц. Так как за каждой компонентой стоит порождающая ее самостоятельная и независимая причина, имеет смысл использовать ее в качестве предиктора [5]. Для этой цели мы применили автокорреляционный анализ статистической обработки данных [6].

Материал и методы исследования

В основу настоящей работы заложены результаты количественных учетов населения модельной группы жуков-жужелиц на ключевом участке Баргузинского хребта в 1988-2008 гг. [7]. Исследование проведено на стационарных площадях в срединной части Баргузинского хребта стандартным методом отлова почвенными ловушками [8] (рис. 1).

Проанализировано 37 динамических рядов популяций 18 массовых видов жужелиц из 11 биотопов. Доминантными считались виды жужелиц, имеющие 5% и более от численного обилия: Pterostichus montanus Motsch., 1844, (26,6% от общего количества отловленных экземпляров), Carabus odoratus barguzinicus Shil, 2000,

(17,3%), Pterostichus dilutipes Motsch., 1844, (16,7%), Calathus micropterus Duft., 1812 (6,2%), Carabus loschnicovi F.-W., 1823 (5,1%). К субдоминантным видам (1-5%) принадлежат: Carabus henningi F.-W., 1817, (4,4%), Pterostichus eximius, Mor.^ 1862 (4,1%), Pterostichus adstrictus Eschs., 1823 (3,1%), Pterostichus orientalis Motsch., 1844

(2,5%), Amara brunnea Gyll., 1810 (2,3%), Amara quenseli Schoenh., 1806 (2,1%), Curtonotus hyperboreus Dej., 1831 (1,9%). В группу фоновых видов (менее 1,0%) вошли: Curtonotus aulicus Panz., 1787, Cicindela sylvatica Linn_n 1758, Amara nitida Sturm. Д&25, Amara ovata F, 1790, Amara similata Gyll., V&\0, Harpahis latus F, 1758 [2, 4, 9].

Высота

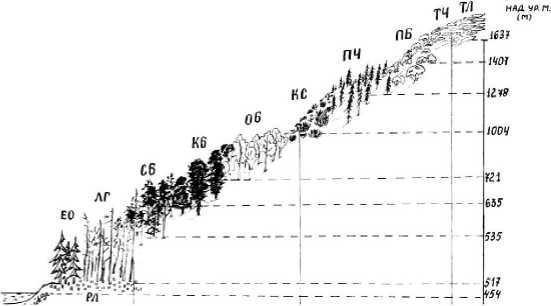
Рис. 1. Схема постоянного трансекта в долине р. Давше (Баргузинский хребет)

Примечания: Обозначения биотопов : РЛ - разнотравный луг, цд.7; ЛГ - лиственничник голубичный, пл.8; ДО - ельник осоковый, пл.9; СБ - сосняк брусничный, пл.10; КБ - кедровник бадановый, пл.И; ОБ - осинник бадановый, пл.12; КС - формация кедрового стланика, пл.13; ПЧ - пихтарник черничный, пл.14; ПБ - парковый березняк, пл.15; ТЧ - тундра черничная, пл.16; ТЛ - тундра лишайниковая, пл.17. Отделы катены : EL - элювиальный, TR - 1 - верхний транзитный, TR - 2 -нижний транзитный, АС - аккумулятивный.

Автокорреляционный анализ

Порядок статистической обработки данных методом автокорреляционного анализа временных последовательностей в программе Excel 2003 состоит из следующих этапов:

• 1.    Массив исходных данных по каждому виду в биотопе формируем следующим образом: располагаем значения среднемноголетней численности вида напротив лет исследования вертикально. Высота каждого столбца пропорциональна частоте наблюдений. Достраиваем по соседству с первым столбцом второй с тем же набором значений (А =20), но смещенный на один шаг (год) вниз. Величина смещения называется лагом (Z) [10]. Формирование все новых выборок связано с уменьшением их размера и сопровождается снижением значимости полученных коэффициентов, поэтому ограничиваем минимальный рекомендованный объем примерно на уровне трети от длины исходного ряда (в нашем случае L = 8) [6].

• 2.    Рассчитываем коэффициент корреляции г\ функции Гк между двумя множествами данных, показывающий степень согласованности одних и тех же чисел. Коэффициент г есть показатель соответствия динамики переменной на соответ

• 3.    Проводим анализ статистических свойств значений полученных автокорреляционных функций. Цель биометрического анализа состоит в том, чтобы избавиться от флюктуаций, выходящих за рамки доверительного интервала. Каждый коэффициент функции показывает, насколько динамика численности данного фрагмента ряда походит на динамику другого участка ряда, отстоящего от него на 1, 2, 3 и т.д. шагов. Сила связи коэффициента корреляции распределяется следующим образом: г > 0,7 считается сильной, г = 0,5-0,7 - средней, г = 0,2-0,5 -слабой. Оценку статистической значимости вычисленных коэффициентов автокорреляционной функции рассчитываем по формуле:

  /эК=П=кИ(_й-2)/^(1-Г²).

• 4.    Графические методы представления анализируемых данных позволяют лучше понять их локализацию и закон распределения. Одной из форм наглядного изображения автокорреляционной функции является коррелограмма. Кроме

ствующем интервале основного ряда. В первом случае используем значения всего начального ряда и сегмента соседнего ряда (у и уда), смещенного на один шаг, а затем повторим операции для последующих рядов, смещенных на два (у и уда), три (у и уда) и т.д. шагов на протяжении выборки. Таким образом, получаем серию коэффициентов корреляции (г_ь г₂, А ...) аргумента к (в нашем случае, это год) при к = 1,2,3,...называемую автокорреляционной функцией. Суть ее такова, что одно и то же значение (на выходе) служит аргументом той же функции (на входе): уда =jy^ к, т.е. моделирование динамики численности происходит на основе только внутрипопуляционных факторов [11]. Величина коэффициента корреляции варьирует от -1 до +1. При к = 0, г₀ = 1 по определению, и это значение исключается из рассмотрения как не несущее информации. Область возможных значений коэффициентов г в исследуемой выборке -доверительный интервал г ± tm_w где t - табличное значение распределения коэффициента Стьюдента (для а = 0,005, df п-2), т,. - стандартная статистическая ошибка коэффициента автокорреляции, рассчитывается по формуле: т_г = "V (1-г²) / (п-2). ‘ '

Сравним полученное значение /_эксп с табличным / - распределения Стьюдента и установим статистически доказанный уровень вероятности (Р) имеющихся значений автокорреляционной функции. К высокому доверительному уровню, согласно данным таблицы, относятся коэффициенты корреляции при Р = 0,002-0,001, к среднему -Р =0,02-0,01, к низкому - Р = 0,10-0,05 [12].

Автокорреляционные функции с коэффициентами г < 0,2, Р < 0,10 в дальнейший анализ не включаются, выбраковываются.

значений самой функции на графике пунктирной линией размещают приблизительный 95% доверительный интервал для всех к + 0, иначе его называют «доверительной трубкой» [6].

Результаты и обсуждение

Форма корреляционной функции позволяет выявить отрезок времени, значения которого повторяются, и делать выводы о периодизме изучаемого процесса. Чем выше доверительный уровень, на котором делается вывод, тем больше уверенность в его обоснованности. Высокие положительные значения г автокорреляционной функции (смещения) обеспечивают значимую коррелированность и доказывают, что ряд периодичен. А наибольшие коэффициенты t по уровню вероятности Р указывают на величину периода Т. Значения автокорреляции, близкие к 0, говорят об ее отсутствии [11].

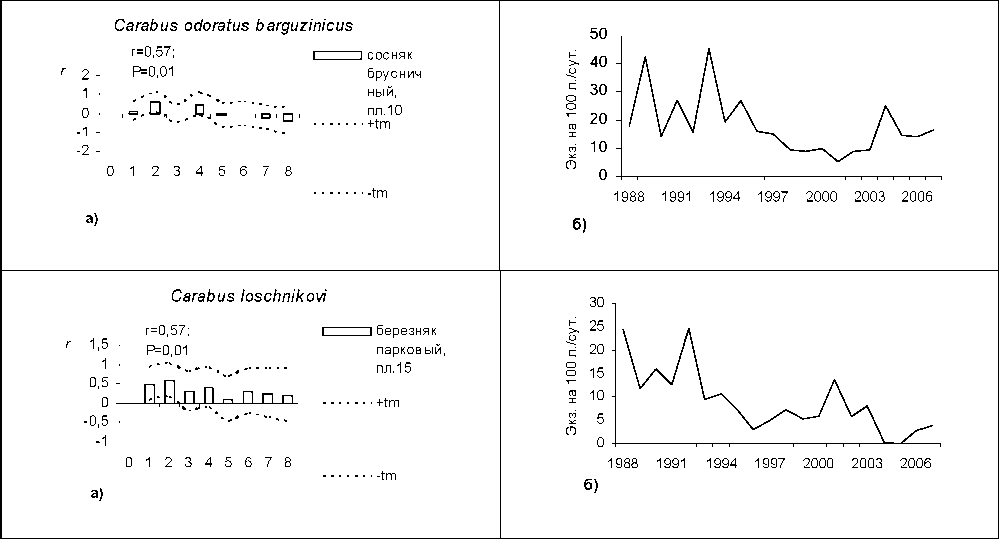
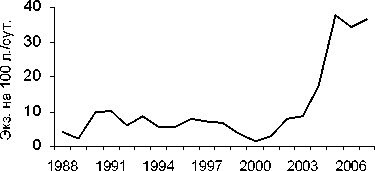
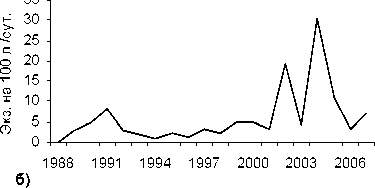
Методом автокорреляционного анализа многолетней динамики численности жужелиц было установлено, что из 37 временных рядов лишь в 16 популяциях, относящихся к 13 видам жужелиц, выявлены периоды с высокой степенью значимости. Если пролонгированный мониторинг динамики численности только показал волновой характер ряда (рис. 26, 36, 46, 56), то использование автокоррелляционного метода анализа в наших расчетах позволило выяснить наличие периодизма и определить величину периода Т (рис. 2а, За, 4а, 5а).

ный, пл.

.......+tm

Carabus henningi r=0,67;                        1        'ЛуГ

. сп пи                         разнотрав

• 1 -

• О -

• ■1 -

• ■2 -

• ........tm

б)

Calathus micropterus

r=0,86; г 2 п Р=0,001

разнотрав ный, пл.7

+tm

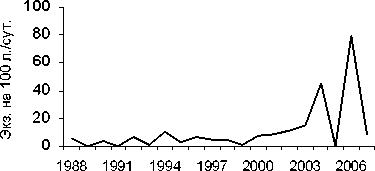
б)

Pterostichus adstrictus

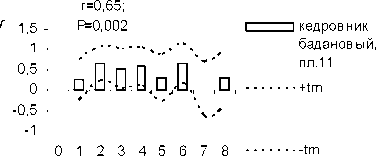
Curtonotus aulicus

-------tm

50 и

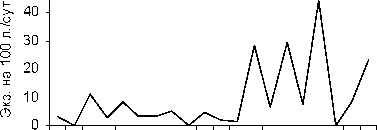
1988 1991 1994 1997 2000 2003 2006

Amara ovata

• ^{1          1 П}У^Г

r             r=0,60;                                  ’

• ^1,5 1    P=0 01                          разнотрав

  12 n

  

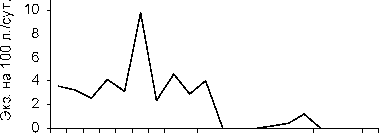
  1988 1991 1994 1997 2000 2003 2006

  
  

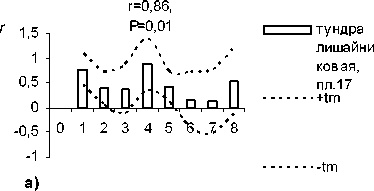
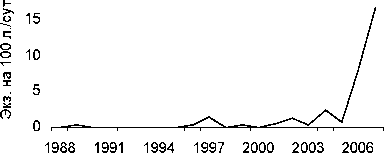
  Pterostichus montanus

  
  
  

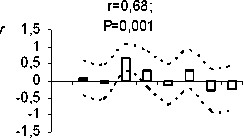
  a)

  
  

  тундра лишайнико вая, пл.17

  
  

  60 и

  
  

  +tm

  
  

  ■tm

  
  

  CD

  
  

  40 -

  20 -

  
  
  

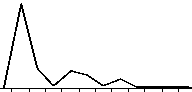
  1988 1991 1994 1997 2000 2003 2006

  
  

  Pterostichus eximius

  
  

  г=0,57; Р=0,01

  
  

  J осинник бадановый, пл.12

  
  
  
  
  
  
  
  
  
  

  0,5 - П П о — Д, ЕЗД, LI ,U ,□ ,□

  -0,5-° ¹ 2 3 4' 5 б'«7,8

  
  

  +tm

  
  

  ■tm

  
  
  
  
  
  

  1988 1991 1994 1997 2000 2003 2006

  
  

  a)

  
  
  
  

  Рис. 3. Коррелограммы динамики численности жужелиц Баргу зинского хребта с периодом Г = 3

  
  

  Cicindela sylvatica

  
  
  
  
  
  

  Pterostichus dilutipes ।      ।

  
  
  
  
  

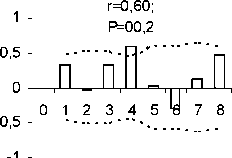
  ничник голубим НЫЙ, пл.8 +tm

  
  
  
  
  

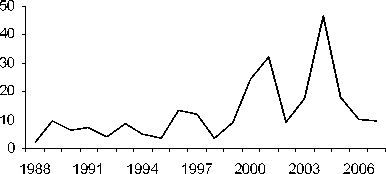
  .......-tm

  
  

  a)

  
  

  Рис. 4. Коррелограммы динамики численности жужелиц Баргузинского хребта с периодом Г = 4

  
  

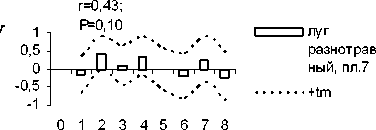
  Amara similata

  
  

  Г 2 _п

  
  

  J луг разнотрав ный, пл.7

  
  

  г=0,53, Р=0,02

  О

  
  
  

  r+tm

  
  

  CD

  
  

  5 0

  
  

  r-tm

  
  

  1988 1991 1994 1997 2000 2003 2006

  
  

  a)

  
  

Рис. 5. Коррелограммы динамики численности жужелиц Баргузинского хребта с периодом Г = 5

Таким образом, способом анализа временных последовательностей методом автокорреляции обнаружены динамические ряды жужелиц с четкой периодичностью. Период Т = 2 отмечен у всех видов рода Carabus: С. odoratus, С. loschnicovi, С. henningi и Calathus micropterus, Pterostichus adstrictus, Curtonotus aulicus, Amara ovata. Период T = 3 зафиксирован у Pterostichus montanus, Pt. eximius; T = ^-Pt. dilutipes, Cicindela sylvatica; T = 5 - Amara similata (рис. 2-5).

В остальных временных рядах видов Pt. orientalis, Am. nitida, Am. quenseli, Harpalus latus все значения коэффициентов автокорреляционной функции оказались недостоверными, периодическая компонента не обнаружена.

Анализируя временные ряды видов жужелиц в разных биотопах, было замечено, что в разных локальных популяциях вида периодическая компонента может проявляться или отсутство вать. Популяция с четкой периодичностью динамического ряда обладает, как правило, высокой плотностью населения со стабильным типом динамики численности и занимает в биотопе лидирующее положение среди других видов. Однако если популяции этого же вида, с низким обилием и продромальным типом динамики численности, в соседнем биотопе занимает подчиненное положение, то четкой периодичности уже не наблюдается. Отсутствие периодической компоненты во временном ряду, возможно, связано с недостаточностью данных для статистического анализа.

Наличие четкой периодичности в многолетнем ряду динамики обилия может свидетельствовать о внутренней устойчивости популяции к влиянию факторов и позволяет спрогнозировать ее численность заранее.