Применение метода дерева решений для решения задач классификации и прогнозирования

Искусственный интеллект является обширной областью науки, алгоритмы которой используются при решении задач, для которых часто сложно и невозможно создать явный алгоритм решения. В настоящее время известно достаточно много алгоритмов, предназначенных для решения задач классификации или прогнозирования: метод опорных векторов, метод k ближайших соседей, нейронные сети и деревья решений [1].

Деревья решений – это способ представления правил в иерархической, последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение [2]. На ребрах дерева записываются атрибуты, от которых зависит целевая функция. Данная статья посвящена одному из классических методов интеллектуального анализа данных– построению деревьев решений. Наиболее общее определение дерева решений – это средство поддержки принятия ре- шений при прогнозировании, которое широко применяется в статистике и анализе данных.

Цель процесса построения дерева принятия решений – создать модель, по которой можно было бы классифицировать случаи и решать, какие значения может принимать целевая функция, имея на входе несколько переменных.

Применения метода дерева решений для решения задач классификации и прогнозирования

Приведем пример построения дерева решений, решив задачу классификации сотрудников магазина. В качестве исходных данных выберем небольшой набор данных – сотрудники магазина, представленный в таблице 1.

В качестве целевой переменной возьмем переменную status; 5 записей из 11 целевая переменная имеет значение senior, а оставшиеся 6 записей – junior.

Таблица 1. Сотрудники магазина

department	status	age, years	salary, thousand rubles
sales	senior	31	46
sales	junior	26	28
sales	junior	31	33
marketing	senior	36	46
marketing	junior	31	41
systems	senior	31	66
systems	junior	26	46
systems	senior	41	66
secretary	senior	46	36
secretary	junior	26	28

Энтропия исходного множества до разбиения составит [3]:

Info = -£ /?7 log2p f = -(5 /11) log2 (5 /11)-

-(6/ll)10g2(6/ll) = 1,023 бит.

Произведем разбиение по атрибуту department. Три записи данного атрибута имеют значение sales, четыре – systems, два – marketing, два – secretary. Соответствующие вероятности будут равны:

p =3/ii- p =4/ii-

^Гsales    0/11, ^rsystems ⁴ ' ^{1 1} ’

p = 2/11- P =2/11

marketing             ’ secretary             *

Одна из трех записей, содержащих значение sales, указывает на senior, а две – на junior. Тогда при случайном выборе из этих трех записей вероятность появления senior составит 1/3, а junior – 2/3. Вычислим энтропию для значения sales:

^sales W = “E РД°№ = “0 1 3) 10§2 0 Z 3) ”

-(2/3) log, (2/3) = 1,35 бит.

Две записи из четырех, содержащих значение systems, указывают на senior, а две – на junior. Вычислим энтропию:

WOsyste^N^-^pfo^Pj =

= -(2 / 4) log, (2 / 4) - (2 / 4) log, (2 / 4) = 1 бит.

Одна из двух записей, содержащих значение marketing, указывает на senior, а другая – на junior. Вычислим энтропию:

M„,₀,_fc„„g(^) = -^РД°§2Р, =

= - (1 / 2) log, (1 / 2) - (1 / 2) log, (1 / 2) = 1 бит.

Одна из двух записей, содержащих значение secretary, указывает на senior, а другая – на junior. Вычислим энтропию:

lnf° secretary = -^p До^р 3 =

= -(1 / 2) log, (1 / 2) - (1 / 2) log, (1 / 2) = 1 бит.

На основе полученных данных можно рассчитать полную энтропию разбиения:

Hbdepartment (TV) = (3 /11) x 1,35 + (4 /11) x 1 +

+ (2/1 l)xl + (2/1 1) x 1 = 1,095 бит.

Прирост информации, полученный в результате разбиения по атрибуту department, будет равен:

Ga™department (N) = ^fa(N) -

- ^n/° department (N) = 1,023 -1,095 = - 0,072 бит.

Аналогичным образом находим и получаем прирост информации по остальным атрибутам:

Gainage (N) = Info(N) - Infoage (N) = 0,659 бит;

Gainsalary (N) = Info (N) - Info5Qlary (N) =

= 0,658 бит.

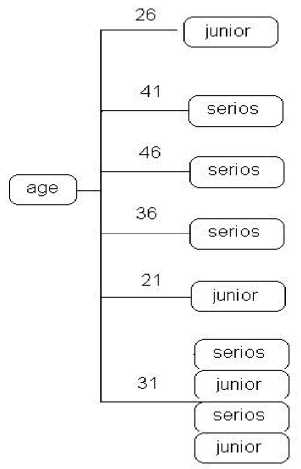
Рис. 1. Результат первого шага построения дерева

Таким образом, прирост информации в результате разбиения по атрибуту age больше по сравнению с другими атрибутами, поэтому выбирается в качестве начального разбиения в корневом узле дерева. Схема начального разбиения представлена на рис. 1.

Для значения 31 год получен узел, содержащий две записи со значением целевой переменно senior и две со значением junior. Далее производим поиск оптимального разбиения данного подмножества (подмножество N 1) данного узла.

Таблица 2. Множество N 1

department	status	age, years	salary, thousand rubles
sales	senior	31	46
sales	junior	31	33
systems	senior	31	66
marketing	junior	31	41

В качестве целевой переменной возьмем переменную status. В двух записях из четырех целевая переменная принимает значение senior и в двух – junior. Поэтому энтропия исходного множества до разбиения составит:

Info(M) = -^/2ylog2^z =

= - (2 / 4) log 2 (2 / 4) - (2 / 4) log 2 (2 / 4) = 1 бит.

Находим прирост информации по каждому нецелевому атрибуту:

Gaindepartmenl (M) = InMM) - Info deparlmem (M) =

= 0,5 бит ;

GainS(1^ (Nl) = Info (ЛП) - Infosalm, (ЛП) =

= 1-0 = 1 бит.

Разбиение по атрибуту salary обеспечивает наибольший прирост информации, поэтому выбирается в качестве дальнейшего разбиения дерева. Полное дерево, полученное в результате разбиения, представлена на рис. 2 [4].

Распространенный способ реализации деревьев решений – это построение дерева на языке программирования Python. Чтобы оценить, насколько хорош выбранный атрибут, алгоритм сначала вычисляет энтропию всей группы. Затем он пытается разбить группу по возможным значениям каждого атрибута и вычисляет энтропию двух новых групп.

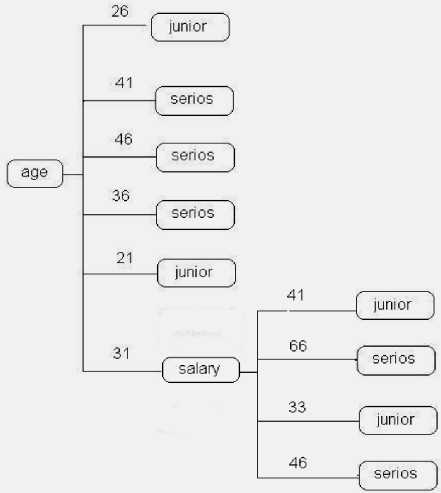
Рис. 2. Полное дерево решений

Для определения того, какой атрибут дает наилучшее разбиение, вычисляется информационный выигрыш, то есть разность между текущей энтропией и средневзвешенной энтропией двух новых групп. Он вычисляется для каждого атрибута, после чего выбирается тот, для которого информационный выигрыш максимален. Вычисляя для каждого узла наилучший атрибут и расщепляя ветви, алгоритм создает дерево [5].

На рис. 3 представлен результат построения дерева решений с помощью интерпретатора языка программирования Python 2.7.6 [6].

Риc. 3. Результат построения дерева решений с помощью Python 2.7

Рассмотрим следующий пример построения дерева решений. В качестве исходных данных выберем классический набор данных – ирисы Фишера. В отличие от предыдущего примера данный набор содержит 150 экземпляров ирисов, принадлежащих к трем видам (setosa, versicolor, virginica). Для каждого экземпляра ириса известны четыре величины: длина и ширина чашелистика, длина и ширина лепестка [7]. Наша задача выработать критерии, по которым можно различить три вида. В качестве целевой переменной возьмем переменную Class; 50 записей из 150 принадлежат атрибуту Iris-setosa, 50 записей – Iris-versicolor, 50 записей – Iris-verginica. Энтропия исходного множества до разбиения составит:

Info^ = -^^ylog2jpy =

= -(50/150)log2(50/150)-(50/150)log2(50/150)-

- (50 /150) log2 (50 /150) = 0,477 бит.

Прирост информации по атрибутам:

Gains-imglh W = lnfo(N) - lnfos_length (N) =

= 0,477-1,383 = -0,906 бит;

Gam .-width (O = !nfo{N) - Infos.wjdth (N) = = 0,477-1,506 = -1,029 бит;

G^p-iength W = NOW - InfOp.length (N) =

= 0,477-0,039 = 0,438 бит;

Gainp-width (^) = Info^N) - Infop_width (N) = = 0,477-0,284 = 0,193 бит.

Прирост информации в результате разбиения по атрибуту petal-length больше по сравнению с другими атрибутами, поэтому выбирается в качестве начального разбиения в корневом узле дерева.

После этого производим дальнейшее разбиение, пока не получим оптимальное разбиение полного множества. Полное дерево, полученное в результате разбиения, представлено на рис. 4.

Чем больше набор данных содержит записей, тем более сложным и трудоемким становится процесс построения дерева решений вручную. Он занимает огромное количество времени, и вероятность ошибок возрастает. Для решения данной проблемы существуют программные продукты, предназначенные для анализа данных и содержащие алгоритм построения деревьев решений.

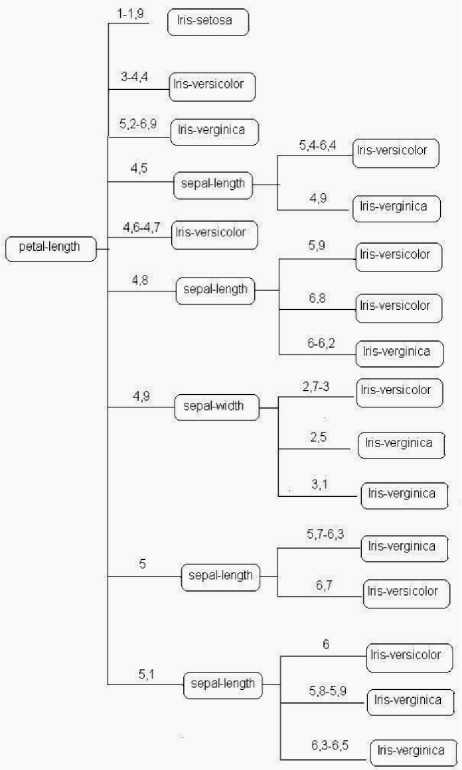
Рис. 4. Полное дерево решений

Одними из самых распространенных программ на сегодняшний день являются Deductor[8] и Orange Canvas [9]. На рис. 6 представлен результат построения дерева решений в Deductor. На рис. 7 представлен результат построения дерева решений в Orange Canvas [10].

Как видно из рис. 6-7, результаты, полученные с помощью программ Deductor и Orange Canvas, соответствуют результатам формульных вычислений. Поэтому можно сделать вывод о том, что задачи (наборы данных) с относительно небольшим числом атрибутов могут решаться вручную, в то время как задачи (наборы данных) с большим числом атрибутов легче и целесообразнее решать с помощью программных систем.

Чем больше набор данных, тем дольше и сложнее становится расчет по формулам. Могут затрачиваться часы, дни и даже месяцы, а программы производит расчеты в течение нескольких секунд. Программа сама отсекает несущественные факторы, выявляет степень влияния тех или иных факторов на результат, а также выдает информацию о достоверности правил дерева м Условие__________________________________| ^ Следствие________| it Поддержка | Д Достоверность |

- •■—:ЕСЛИ		■I 142 I—	____| 49
1—       petal_length < 2,45	J Iris-setosa               I — ______	_] 45H**_	■I 45
В ■■ petal-length >= 2,45	I—	_| 97 |—	ZZI 49
ы !■■! petal_width < LA	иве___	_| 53 1—	ZZ1 48
^— petal-length < 4,9b - ■■■! petal-length >= 4.95	Iris-versicolor I!_______________________	_| 47 |— ZJ 6|—■*—	J 48 1 4
^™ petal width < 1,55	lris-v»ginica	3 1— —	■I 3
:—BJ petal—width >=1,55	Iris-versicolor	_| 3 1— —__	__I 2
[■■l petal_width >= I,/5	Itis-virginica                 |— _______	_| 44 I	■ I 43

Рис. 6. Результат построения дерева решений в Deductor решений. Кроме того, полученные результаты, представленные в программах, являются более простыми для восприятия и понимания.

Результаты, полученные с помощью Orange Canvas и Deductor, обладают примерно равными возможностями. Однако работа с деревьями решений в Deductor реализована заметно удобнее. Программа имеет несколько визуализаторов дерева решений.

Пользователь может выбрать наиболее удобный для понимания. Один из визуализа- торов Deductor – правила «если – то» – удобное представление построенного дерева в виде правил.

Заключение

В статье рассмотрены несколько вариантов реализации алгоритма деревьев решений на конкретных примерах решения задач.

Качество работы метода деревьев решений зависит как от выбора метода, так и от набора исследуемых данных.

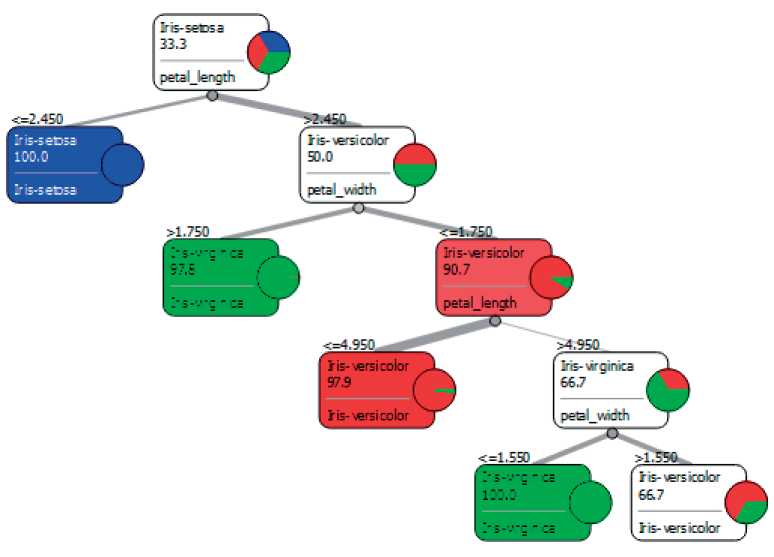
Рис. 7. Результат построения дерева решений в Orange Canvas