Применение метода двойной аппроксимации для построения матриц жесткости объемных конечных элементов
Автор: Гайджуров П.П., Савельева Н.А.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Механика
Статья в выпуске: 4 т.23, 2023 года.
Бесплатный доступ
Введение. При численном решении задач теории упругости в трехмерной постановке методом конечных элементов применяются конечные элементы (КЭ) в форме параллелепипедов, призм и тетраэдров. Обычно построение матриц жесткости объемных КЭ базируется на принципе изопараметричности, суть которого состоит в использовании для аппроксимации геометрии и перемещений полиномов Лагранжа. В расчетной практике наибольшее распространение получили так называемые полилинейные изопараметрические КЭ с линейным законом аппроксимации перемещений. Главный недостаток данных элементов кроется в эффекте «loсking» («запирания») при моделировании изгибных деформаций. Причем погрешность численного решения существенно возрастает в случае, когда конструкция, по сравнению с обычными деформациями, претерпевает значительные смещения как жесткое целое. Многолетний опыт решения задач механики деформируемого твердого тела методом конечных элементов показал, что существующие объемные КЭ обладают медленной сходимостью при моделировании изгибных деформаций пластин и оболочек. Цель настоящего исследования состоит в построении на основе метода двойной аппроксимации матриц жесткости полилинейных объемных КЭ повышенной точности, позволяющих учитывать жесткие смещения.Материалы и методы. Для построения матриц жесткости объемных КЭ применен математический аппарат метода двойной аппроксимации, суть которого состоит в раздельном представлении функций распределения перемещений и деформаций внутри элемента. Хранение и обработка результирующей системы уравнений реализованы в алгоритмических терминах разреженных матриц. Разработка программного обеспечения и проведение вычислительных экспериментов осуществлены с использованием 64-х разрядной вычислительной платформы Microsoft Visual Studio 2013 и компилятора Intel® Parallel Studio XE 2019 со встроенным текстовым редактором Intel® Visual Fortran Composer XE 2019. Визуализация результатов расчетов выполнена с помощью дескрипторной графики пакета компьютерной математики Matlab. В качестве тестового образца использован объемный восьмиузловой КЭ SOLID185 программного комплекса ANSYS Mechanical.Результаты исследования. Разработано математическое и программное обеспечение для исследования напряженно-деформированного состояния массивных конструкций при различных видах внешнего воздействия. На тестовых примерах с известными аналитическими решениями выполнена верификация авторизированного пакета прикладных программ. Показано, что построенные КЭ по точности удовлетворяют основным требованиям, предъявляемым к конечно-элементному моделированию пространственных задач теории упругости.Обсуждение и заключение. Проведенное тестирование разработанного математического и программного обеспечения показало, что построенные на основе метода двойной аппроксимации конечные элементы успешно конкурируют с аналогичными объемными элементами SOLID185 программного комплекса ANSYS Mechanical. Предлагаемые элементы могут быть интегрированы в отечественные импортозамещающие программные комплексы, реализующие метод конечных элементов в форме метода перемещений.
Метод конечных элементов, моментная схема метода конечных элементов, метод двойной аппроксимации, объемные конечные элементы, тестирование конечных элементов
Короткий адрес: https://sciup.org/142239832
IDR: 142239832 | УДК: 539.42 | DOI: 10.23947/2687-1653-2023-23-4-365-375
Текст научной статьи Применение метода двойной аппроксимации для построения матриц жесткости объемных конечных элементов
Original article Application of the Double Approximation Method for Constructing Stiffness Matrices of Volumetric Finite Elements
Peter P. Gaidzhurov , Nina A. Saveleva
Introduction . When numerically solving problems of elasticity theory in a three-dimensional formulation by the finite element method, finite elements (FE) in the form of parallelepipeds, prisms and tetrahedra are used. Regularly, the construction of stiffness matrices of volumetric FE is based on the principle of isoparametricity, which involves the Lagrange polynomials to approximate the geometry and displacements. In computational practice, the most widespread FE are the so-called multilinear isoparametric FE with a linear law of approximation of displacements. The main disadvantage of these elements lies in the “locking” effect when modulating bending deformations. Moreover, the error of the numerical solution increases drastically in the case when the structure, in comparison to conventional deformations, undergoes significant displacements as a rigid whole. Long-term experience in solving problems of deformable solid mechanics by the finite element method has shown that existing volumetric FE have slow convergence, specifically, when modeling bending deformations of plates and shells. This study aims at constructing stiffness matrices of multilinear volumetric FE of increased accuracy allowing for rigid displacements based on the double approximation method.
Materials and Methods . The mathematical apparatus of the double approximation method based on the principle of a separate representation of the distribution functions of displacements and deformations inside the element, was used to construct the stiffness matrices of volumetric FE. The storage and processing of the resulting system of equations was implemented in algorithmic terms of sparse matrices. Software development and computational experiments were carried out using the Microsoft Visual Studio 2013 64-bit computing platform and the Intel ® Parallel Studio XE 2019 compiler with the integrated Intel ® Visual Fortran Composer XE 2019 text editor. Visualization of the calculation results was performed using the descriptor graphics of the MATLAB computer mathematics package. A large eightnode SOLID185 CE of the ANSYS Mechanical software complex was used as a test sample.
Results. Mathematical tool and software were developed to study the stress-strain state of massive structures under various types of external actions. The authorized application software package was verified on test examples with known analytical solutions. It has been shown that the constructed FE accurately satisfy the basic requirements for finite element modeling of spatial problems of elasticity theory.
Discussion and Conclusion . The performed testing of the developed mathematical and program toolkit has shown that the finite elements constructed on the basis of the double approximation method can successfully compete with similar SOLID185 volumetric elements of the ANSYS Mechanical software complex. The proposed elements can be integrated into domestic import-substituting software systems that implement the finite element method in the form of the displacement method.
Введение . При конечно-элементном моделировании напряженно-деформированного состояния массивных тел используются объемные конечные элементы (КЭ) в форме параллелепипедов (гексаэдров), призм и тетраэдров, построение матриц жесткости которых выполнено, как правило, по изопараметрической технологии [1–5]. Вместе с тем известно, что полилинейные изопараметрические КЭ при использовании однослойной схемы неудовлетворительно моделируют изгибные деформации даже при существенном сгущении сетки [6, 7]. Суть данной проблемы состоит в эффекте « locking » («запирания») элемента вследствие так называемой деформации «ложного сдвига» [8, 9]. Для «улучшения» изопараметрических КЭ используют аппарат несовместных элементов, созданных путем введения дополнительных неузловых степеней свободы или вспомогательных аппроксимирующих полиномов [8]. Вместе с тем наиболее эффективным способом решения проблемы «заклинивания» КЭ является применение моментной схемы метода конечных элементов, теоретические основы которой были разработаны А.С. Сахаровым [7]. В последующем данный подход получил название метод двойной аппроксимации (МДА) [6]. Концептуально МДА базируется на раздельном представлении функций распределения перемещений и деформаций внутри элемента. Целью настоящего исследования является построение на базе МДА и тестирование новых объемных полилинейных КЭ, позволяющих моделировать поведение различных конструкций при различных видах внешнего воздействия.
Материалы и методы. Рассмотрим семейство объемных КЭ, состоящее из восьмиузлового и шестиузлового элементов, в глобальных декартовых осях zm , m = 1, 2, 3 (рис. 1). Геометрию и перемещения КЭ представим в следующем виде: ne ne zm = E zk Ф (x 1, x 2 , x 3 ) ; um = E uk Ф (x 1, x 2 , x 3 ) ,
= 1 к = 1
где z(k), u k) — узловые координаты и перемещения; ф k (x 1, x 2, x 3) — «функции формы», представляющие собой произведение одномерных полиномов Лагранжа первой степени; x 1 , x 2 , x 3 — локальные в общем случае неортогональные координаты КЭ; n e — число узлов элемента. Для базового восьмиузлового элемента
(рис. 1 а ) n e = 8 «функции формы» определяем по формуле:
Ф k ( Х 1 , Х 2 , X 3 ) = П (1 + Prk xr ) , (1)
8 r = 1
здесь p rk — координаты узлов в локальных осях. Значения p rk задаем в форме матрицы:
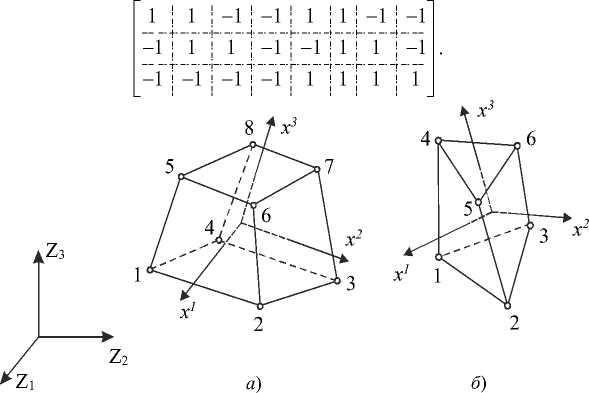
Рис. 1. Объемные КЭ: а — восьмиузловой; б — шестиузловой
Зависимость между ковариантными компонентами тензора деформаций в локальном базисе и перемещениями в глобальных осях имеет вид [7]:
8 = — ( z - u . + z . u ij 2 m , j m , i m , i m , j ,
(суммирование по повторяющемуся индексу)
где z m , s =d z m / d x s ; u m , s =d u m / d Xs , s = i, j .
Механика
Связь между вектором деформаций { е } и вектором узловых перемещений { w } представим в матричной форме:
{е} = [ D ]{w}, где блочная матрица [D] — [[D]i [D]2 .[D]ne ] ;
(6 x П е )
субматрица
[D]к =[{D«}k {D(2)}k {D(3)}k] , к —1,2,...,пе.
(6 x 3)
Выражения для вектор-столбцов рассматриваемых КЭ имеют следующий вид [10]: восьмиузловой элемент
(рис. 1 а ):
Рм I Z , + ГZ + Z л p.Лх. -v(Z n + Z , p., )x. + p 1 к [ m ,1 m ,12 m ,1 p 2 к 2 m ,13 m ,1 p 3 к3
+(Z m + z 1O p.. + Z npM-vz A p., р.Л x. x. l m ,123 m ,12 p 3 к m ,13 p 2 к m ,1 p 2 к p 3 к2 3 ]
р^. I z ,+(z ,,+Z -р.Лх.лЛг ,,+z ,р,Лх.>л-p 2к [ m,2 m,12 m,2 p 1 к 1 m,23 m,2 p 3к3
/ zv zv zv zvX
+ ( z m ,123 + z m ,12 p 3 к + z m ,23 P 1 к + z m ,2 P 1 к P 3 к ) X 1 x 3 ]
Рм I Z .A-(z ,1 + Z . Pm (Z ..-vz . р.Лх. -v
{ D ( m ) } к — 1 <
p 3к [ m,3 m,13 m,3 p 1 к 1 m,23 m,3 p 2к2
+ (Z + Z npM-VZ Pm + Z .Pi/Po/)^^ l m,123 m,13 p 2к m,23 p 1 к m,3 p 1 к p 2к 12 z m,1 p 2к + z m,2 p 1 к + (Z m,13 p 2к + Z m,1 p 2к p3к + z m,23 p 1 к + + Z m ,2 p 1 кР 3 к ) x 3
Z m ,1 p 3 к + Z m ,3 p 1 к + ( Z m ,12 p 3 к + Z m ,1 p 2 к p 3 к + Z m ,23 p 1 к +
+ Z m ,3 p 1 k P 2 к ) x 2
Z m ,2 p 3 к + Z m ,3 p 2 к + ( Z m ,12 p 3 к + Z m ,2 p 1 к p 3 к + Z m ,13 p 2 к + + Z m ,3 p 1 k P 2 к ) x 1
шестиузловой элемент (рис. 1 б ):
r^
Z
r^
Z
r^
Z
z*/ m ,1 Ф к ,1
z*/ i,2 Ф к,2
z*/
,3 Ф к ,3 "
z*x z*/
{ D ( m ) }
к = 8
r^
Z
-
V -
+ ( Z m ,13 Ф к ,1
(
Z m ,23 Ф к ,2
(
Z m ,13 Ф к ,3 "
z*/ m,23 Ф к,3
Z*/ Z*/
-
V -
m ,1 Ф к ,13 ) X 3
m ,2 Ф к ,23 ) X:
-
V -
Z*/ Z*/ X
Z m ,3 Ф к ,13-
Ф к ,23 ) X 2
-™-
,1 Ф к ,2 + Z m ,2 Ф к ,1
+ ( Z
-
V -
-
V -
m ,13 Ф к ,2 + Z
z*/
,1 Ф к ,23 +
.
z*/ Z*/ z*/
Z
m
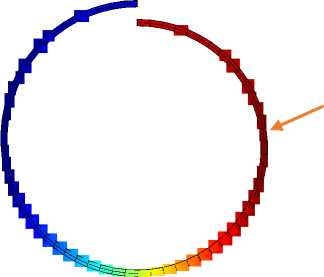
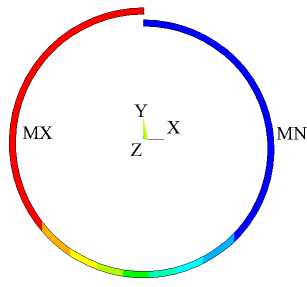
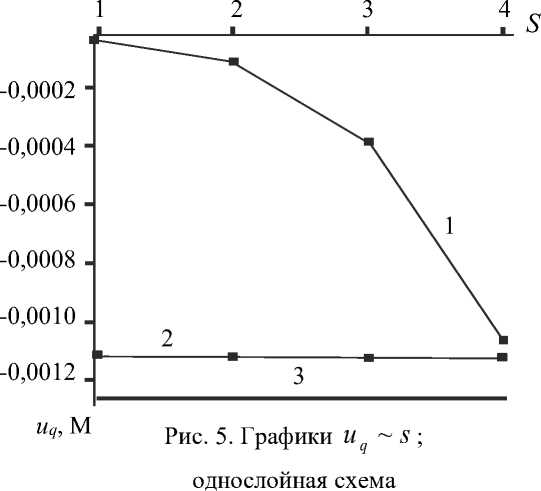
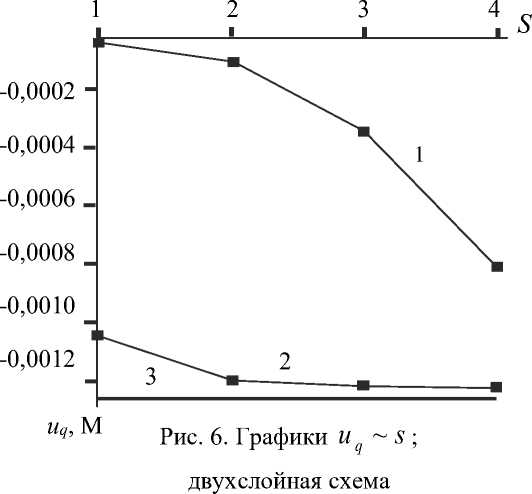
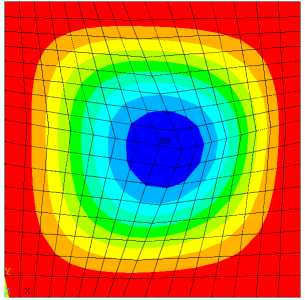
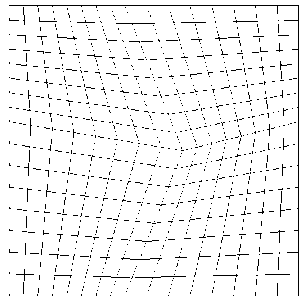
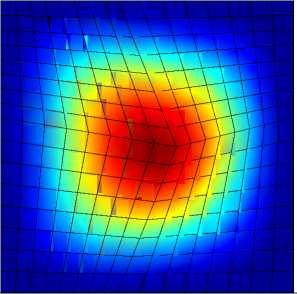
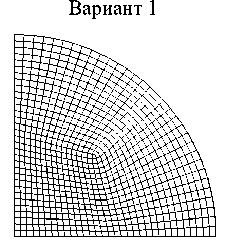
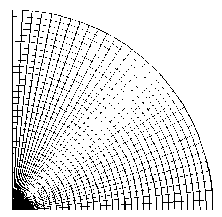
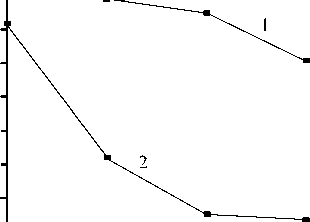
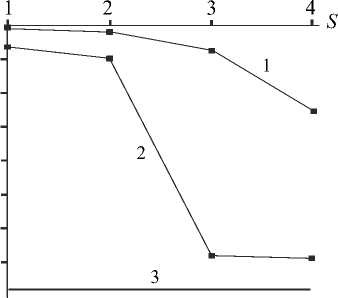
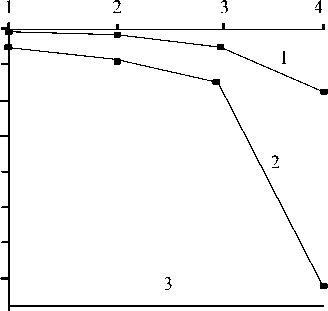
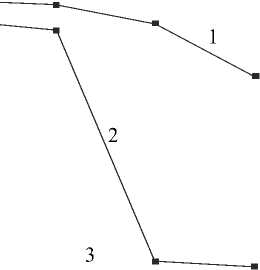
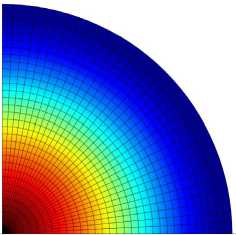
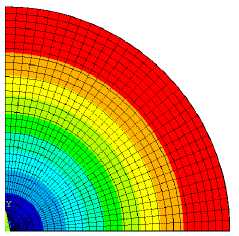
,23 к,1 + Z r^ Z r^ Z z*/ 1 Ф к ,3 z*/ m,2 Фк,13 ) X 3 Z*/ Z*/ m,2 Фк,3 + Z V - m,3 Фк,1 z*/ m,3 Ф к,2 Здесь введены обозначения: •^ Z m, a dim dx a z m,123 XXX , Zm, ap = =0 a3z m d x 1 d x2d x3 a2z m a x a a x p . ' 1 — X 2 — X 3 —0 ; =0 •^ Ф =£r_ к,a d X a * 1 — X 2 — X 3 —0 ; - =d Ф к Ф к, ap z., z., a x a a x p ; a, Р =1,2,3. * 1 =X2=X3=0 Выражения для «функций формы» Ф к (x1, x2, x3) шестиузлового КЭ, полученные на основании полинома (1) с помощью принципа «вырождения», имеют следующий вид: Ф1 =1 (1 +p 11x 1)(1 +p 21x 2)(1+p 31x 3); Ф2 =1 (1 +p 12X1 )(1 +p 22X2 )(1 +p32X3 ) ; p3 = 8 [(1 +Р13x 1 )(1 +Р 23x2 )(1 +Р33x3 ) + (1 +Р14x 1 )(1 +Р24x2 )(1 +Р34x3 )] ; : 1 (1 + Р15x 1 )(1+ Р 25x 2 )(1+ Р 35 x3 ) ; *^ 4 = *^ P 5 = 1 (1+р 16 x i )(1+ p 26 x 2 )(1+p 36 x з); P6 =1[(1 +Р17x 1 )(1 +Р27x2 )(1 +Р37x3 ) + (1 +Р18x 1 )(1 +Р28x2 )(1 +Р38x3 )] . Формулы (2) и (3) являются основой для построения матриц жесткости рассматриваемых КЭ. Соответствующее программное обеспечение разработано на базе вычислительной платформы Microsoft Visual Studio и компилятора Intel® Parallel Studio XE с встроенным текстовым редактором Intel® Visual Fortran Composer XE. Процессы хранения и обработки глобальной матрицы жесткости реализованы в терминах разреженных матриц [11]. Для визуализации результатов расчетов использована дескрипторная графика компьютерной системы Matlab. Результаты исследования. Исследование точности и сходимости разработанного конечно-элементного алгоритма выполнили на тестовых примерах, имеющих аналитическое решение. В тестовых примерах приведены численные решения, полученные с использованием разработанных элементов и аналогичного по размерности элемента SOLID185 программного комплекса ANSYS Mechanical [5, 11]. Ниже приведены примеры, подобранные таким образом, чтобы в них присутствовало сочетание изгибных деформаций и жестких смещений КЭ. Пример 1. Разрезное кольцо, жестко закрепленное в одном сечении и загруженное сосредоточенной силой на свободном конце. Расчетная схема кольца показана на рис. 2. Исходные данные: средний радиус R = 0,2 м; размеры поперечного сечения 0,2*0,2 см; модуль упругости Е = 1011 Н/м2; коэффициент Пуассона v = 0,3; сосредоточенная сила F = 10 Н. Прогиб в точке приложения силы по теории кривых стержней (точное решение) составляет [7]: = F п R3= 10 ■ 3,14 ■ 0,23 f = EJ ~ 1^1011■ 8,333-10' 10 = –0,00302 м. Рис. 2. Расчетная схема разрезного кольца Результаты сходимости представлены в таблице 1. Таблица 1 Результаты сходимости для разрезного кольца Сетка f / 5, м / % МДА ANSYS 2×2×32 –0,00170 / 44 –0,000433 / 86 2×2×64 –0,00292 / 3,3 –0,00125 / 59 2×2×128 –0,00293 / 3 –0,00251 / 17 В таблице 1 в числителе приведено значение прогиба f, в знаменателе — относительная погрешность 5 . Механика Визуализация перемещений uy , полученная на базе МДА и ANSYS на сетке 2×2×64, представлена на рис. 3 и 4. Отметим, что поле вертикальных перемещений, полученное с помощью ANSYS, не отражает зоны с экстремальным значением u y = –0,00314 м, показанной на рис. 3 стрелкой. Рис. 3. Картина распределения u y (МДА) uy , м -0,003138 -0,002456 -0,001793 -0,001121 -0,0004484 0,0 Рис. 4. Картина распределения u y (ANSYS) uy, м -. 001186 -. 001026 -. 865E-03 -. 705E-03 -. 545E-03 -. 385E-03 -. 225E-03 -. 646E-04 -. 001346 . 956E-04 В данном примере особенно отчетливо прослеживается важность учета жестких смещений. Пример 2. Квадратная пластина, жестко защемленная по контуру и нагруженная равномерно распределенной нагрузкой. Исходные данные: длина стороны а = 1 м; толщина h = 0,01 м; модуль упругости Е = 105 Н/м2; коэффициент Пуассона ν = 0,25. Точное значение прогиба в центре пластины определяется по формуле [12]: где α = 0,00126; D= Eh3 12(1 -ν2) uq qa =α D цилиндрическая жесткость; q = 0,00888889 Н/м2 интенсивность распределенной нагрузки. Точная величина uq (в метрах) равна коэффициенту α . В данном примере рассматривалась ¼ часть пластины с учетом условий симметрии. Результаты сходимости в виде графиков uq ~ s для однослойной и двухслойной моделей представлены на рис. 5 и 6. Здесь и далее под слоями подразумевается разбивка пластины на КЭ по толщине. На этих рисунках значения параметра s 1, 2, 3, 4 соответствуют сеткам: 4×4, 8×8, 16×16, 32×32. Приведенные графики отображают результаты решения, полученные с помощью ANSYS (линия 1) и МДА (линия 2). Горизонтальная линия, обозначенная цифрой 3, соответствует точному решению. Из рис. 5 следует, что при однослойной схеме разбивки значения относительной погрешности на сетке 32×32 составляют: SOLID185 — 16 %; МДА — 10,5 %. При использовании двухслойной схемы (рис. 6) на сетке 32×32 имеем: SOLID185 — 36 %; МДА — 2,8 %. Патч-тестирование КЭ выполнено для схемы разбивки 16×16×2 с искажением сетки (рис. 7). Результаты патч-теста в виде картин распределения прогибов uz приведены на рис. 8 и 9. Рис. 8. Распределение u (SOLID185) q -. 958E-04 -. 851E-04 -. 745E-04 -. 639E-04 -. 532E-04 -. 426E-04 -. 319E-04 -. 213E-04 -. 106E-04 0 Рис. 7. Схема разбивки пластины для патч-теста uq , м uq , м -0,001263 -0,001010 -0,0007575 -0,0005050 -0,0002525 0,0 Рис. 9. Распределение u (МДА) q Как видно из рисунков, искажение сетки при использовании SOLID185 приводит к более заметной асимметрии поля uz , чем при использовании МДА. При этом значение максимального прогиба для КЭ МДА uq = 0,001263 м совпадает с точным решением. Пример 3. Круглая пластина, жестко защемленная по контуру и нагруженная равномерно распределенной нагрузкой. Радиус и толщина пластины: R = 1 м; h = 0,01 м. Механические константы аналогичны данным примера 2. Механика Точное значение прогиба в центре пластины определяется по формуле [12]: u q 1 qa4 64 D При значении интенсивности распределенной нагрузки q = 0,00888889 Н/м2 значение uq = 0,01563 м. В процессе тестирования были использованы два варианта дискретизации ¼ части пластины (сектора) на КЭ. В первом варианте три стороны сектора делились на равное число отрезков. Второй вариант базировался на радиальной регулярной схеме разбивки сектора. При этом число элементов вдоль радиуса и циркульной части сектора принималось одинаковым. Рассмотренные варианты дискретизации сектора для сетки 32×32 приведены на рис. 10. Вариант 2 Рис. 10. Варианты дискретизации сектора круглой пластины на КЭ: 1 — равномерная разбивка трех сторон сектора; 2 — радиальная регулярная разбивка Результаты сходимости в виде графиков uq ~ s для дискретизации ¼ части пластины по варианту 1 при однослойной и двухслойной схемах разбивки представлены соответственно на рис. 11, 12 и рис. 13, 14. S - 0,002 - 0,004 - 0,006 - 0,008 - 0,010 - 0,012 1 2 3 4 - 0,014 3 uq, M Рис. 11. Графики uq ~ s для варианта 1; однослойная схема uq, M -0,002 -0,004 -0,006 -0,008 -0,010 -0,012 -0,014 Рис. 12. Графики uq ~ sдля варианта 2; однослойная схема На этих рисунках значения параметра s 1, 2, 3, 4 соответствуют сеткам 4×4, 8×8, 16×16, 32×32. Как и в примере 1, линия 1 соответствует решению на базе SOLID185, а линия 2 — МДА. Горизонтальная линия, обозначенная цифрой 3, соответствует точному решению. Из приведенных графиков следует, что элемент, построенный по моментной схеме на сетке 32×32×2 вариант 2, имеет относительную погрешность 4 %. Картины визуализации поля распределения вертикальных перемещений u z для МДА и SOLID185 при радиальной схеме разбивки ¼ пластины (сетка 32×32×2) показаны соответственно на рис. 15 и 16. -0,002 -0,004 -0,006 -0,008 -0,010 -0,012 -0,014 uq, M S Рис. 13. Графики uq ~ s для варианта 1; двухслойная схема 0+ -0,002 4 -0,004 -^ -0,006 -^ -0,008 -0,010 -0,012 -0,014Н uq, M 4S uz, м -0,01503 -0,01202 -0,009016 -0,006011 -0,003005 0,0 Рис. 15. Распределение u z (МДА) Рис. 16. Распределение u z (SOLID185) Рис. 14. Графики uq ~ sдля варианта 2; двухслойная схема uz, м Из приведенных рисунков видно, что несмотря на качественное совпадение картин u z , относительные погрешности для максимального прогиба составляют: МДА — 3,8 %; SOLID185 — 71 %. Такая значительная погрешность при использовании SOLID185 объясняется тем, что разработчики использовали для аппроксимации геометрии и перемещений шестиузлового КЭ «функции формы» аналогичные функциям, примененным для восьмиузлового элемента, т. е. без принципа «вырождения» [7]. Обсуждение и заключение. Построенные на базе метода двойной аппроксимации матрицы жесткостей объемных полилинейный конечных элементов позволяют моделировать напряженно-деформированное состояние строительных конструкций произвольной геометрии при различных видах внешнего воздействия. Принципиальным отличием предлагаемой концепции от ранее известных конечно-элементных технологий является то, что перемещения в данном случае задаются в глобальных координатах, а компоненты тензора деформаций определяются в местных, в общем случае, неортогональных осях. На тестовых примерах показано, что объемные конечные элементы, построенные по методу двойной аппроксимации, обладают устойчивой сходимостью и успешно конкурируют с элементом аналогичного типа SOLID185 вычислительного комплекса ANSYS Mechanical. Разработанное математическое обеспечение может быть внедрено в отечественные импортозамещающие программные комплексы, реализующие метод конечных элементов в форме метода перемещений.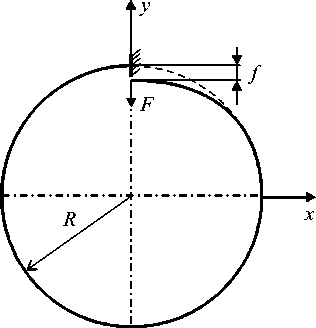



Список литературы Применение метода двойной аппроксимации для построения матриц жесткости объемных конечных элементов
- Zienkiewicz O.C., Taylor R.L. The Finite Element Method, Fifth edition. Oxford, UK: Butterworth-Heinemann; 2GGG. 7G8 p.
- David V. Hutton. Fundamentals of Finite Element Analysis. New York, NY: McGraw Hill Companies; 2004. 494 p. URL: https://wp.kntu.ac.ir/fz kalantary/Source/Finite%2Gelement%2Gmethod/BooksNumerical/Fundamentals%2Gof%2GFinite%o2GEl ement%2GAnalysis,%2GHutton%20(2004).pdf (дата обращения: 15.08.2023).
- Daryl L. Logan. A First Course in the Finite Element Method. New York, NY: CL Engineering; 2011. 836 p. URL: https://kntu.ac.ir/DorsaPax/userfiles/file/Mechanical/OstadFile/dr nakhodchi/DarylL.LoganAFirstCourse.pdf (дата обращения: 15.08.2023).
- Carlos A. Felippa. Introduction to Finite Element Methods. Boulder, CO: University of Colorado; 2004. 791 p. URL: https://vulcanhammernet.files.wordpress.com/2017/01/ifem.pdf (дата обращения: 15.08.2023).
- Saeed Moaveni. Finite Element Analysis. Theory and Application with ANSYS. Hoboken, NJ: Prentice Hall; 1999. 527 p. URL: http://ftp.demec.ufpr.br/disciplinas/TM738/Livros/Finite%20Element%20Analysis,%20Theory%20and% 20application%20with%20ANSYS,%20.pdf (дата обращения: 15.08.2023).
- Голованов А.И., Тюленева О.Н., Шигабутдинов А.Ф. Метод конечных элементов в статике и динамике тонкостенных конструкций. Москва: Физматлит; 2006. 391 с.
- David V. Hutton. Fundamentals of Finite Element Analysis. New York, NY: McGraw-Hill; 2004. 505 p. URL: https://wp.kntu.ac.ir/fz kalantary/Source/Finite%20element%20method/BooksNumerical/Fundamentals%20of%20Finit e%20Element%20Analysis,%20Hutton%20(2004).pdf (дата обращения: 15.08.2023).
- Miguel Luiz Bucalem, Klaus-Jürgen Bathe. The Mechanics of Solids and Structures - Hierarchical Modeling and the Finite Element Solution. New York, NY: Springer; 2011. 597 р.
- Jacob Fish, Ted Belytschko. A First Course in Finite Elements. Hoboken, NJ: Wiley; 2007. 319 p.
- Гайджуров П.П. Конечные элементы повышенной точности для решения трехмерных задач теории упругости. Известия вузов. Северо-Кавказский регион. Технические науки. 2003;(1):54-57. URL: https://cyberleninka.ru/article/n/konechnye-elementy-povyshennoy-tochnosti-dlya-resheniya-trehmernyh-zadach-teorii-uprugosti/viewer (дата обращения: 15.08.2023).
- Чигарев А.В., Кравчук А.С., Смалюк А.Ф. ANSYS для инженеров. Справочное пособие. Москва: Машиностроение; 2004. 512 с. URL: https://www.researchgate.net/profile/AKravchuk/publication/262729610 ANSYS -dla inzenerov/links/0f31753b4294b13fc9000000/ANSYS-dlainzenerov.pdf (дата обращения: 15.08.2023).
- Madenci E., Guven I. The Finite Element Method and Applications in Engineering Using ANSYS. New York, NY: Springer; 2015. 664 p.


