Применение метода F-преобразования для прогноза компоненты векторного тренда и числового представления временного ряда

Нечеткое сглаживание временных рядов на основе нечеткого преобразования ( F- преобразования) — методика, разработанная И. Перфильевой [1], которая может быть отнесена к методикам нечеткого приближения. Нечеткое преобразование ( F -преобразование) представлено для непрерывных функций и функций на ограниченном наборе точек.

Предположим, что функция f известна в точках p 1 ,...,p _N е w . Мы делим интервал w на множество равноудаленных узлов– x _k = u _L +h(k - 1 ),k = 1,... ,n ,

F k+1 = aF k + eF k — р

R k+1 = aR k + eR k — p

Y' = F k+p + R k+p

Для конкретной реализации F- преобразования был выбран следующий вид базисных функций:

, / _x x ^{— x}_k,

A, (x) =------k-^-,еслис, , < x < x, k X /                                     k 1                k xk - xk -1

,   uR - uL где N > n,h      — фиксированной длины. F- n — 1

преобразование имеет две фазы.

Прямое F -преобразование. Определим n базисных функций A 1 ,...,A _n , которые покрывают w и разделим его на n неясных областей. Базисная функция должна удовлетворять следующим условиям (к = 1,... ,n) :

• 1.    A k : w ^ [0,1],A k (X k ) = 1 ,

• 2.    A _k (x) = 0 if x t (x _{k — 1} ,x _k+1 ) , где мы формально полагаем x ₀ = x 1 = u _L , x _{n+ 1} = x _n = u _R ,

• 3.    A _k (x) непрерывна,

• 4.    A _k (x) монотонно возрастает на [ x _{k — 1} ,x _k ] и монотонно убывает на [x _k , x _{k+ 1} ] ,

• 5.    S A k (x) = ¹ для всех x е w •

Используя базисные функции, мы преобразуем данную функцию f в кортеж из n действительных чисел [ F 1 ,...,F _n ] , определенных

X fP 2 A k ⁽P z 2 S Ap)

k = 1

. ,n

Построение модели ВР для генерации числовых оценок прогноза F, R и у по формуле линейной комбинации:

, ( X     ^x i-+1 ^{— x}             .

A , ( x ) = —^k-1-----, еслиx, <  x <  x,₊₁

k                                 k            k + 1

x k+ 1 ^- x k

A _k ( x ) = 0, в противном случае

Далее строится матрица нечеткого разбиения и производится F -преобразование. F -компоненты представляют собой тренд временного ряда.

Вычисляются остатки — разность между трендом и исходным временным рядом:

• r. = Л- Ft.

Прогноз F ( _{n+ 1} ) -ой компоненты реализован несколькими методами:

• - на основании системы двух линейных уравнений

F k — 1 = aF k — 2 + eF k — з +Y F k - 4      (2)

Найдя a , в, Y

^F k+1 = ^aF k ^{+ eF} k — 1 +Y ^F k-2 .

– использованием нейронной сети

Для обучения сети и прогнозирования строилась регрессия: F _{k+ 1} = aF _k + eF k — 1 +Y F k2. .

Для получения числового прогноза временного ряда необходимо сложить обратное F -преобразование с остатками. Остатки для прогноза получаются при помощи системы линейных уравнений, аналогичной (2).

Для оценки качества прогноза вычисляется критерий MAPE :

Романов Антон Алексеевич, аспирант.

1 n

MAPE = -У n²^

у

*100%

Также приводится оценка по критерию SMAPE:

n

SMAPE = - У n t= 1

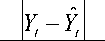
A

( Y + Y )/2

*100%

При его минимальном значении в автоматическом режиме делается вывод об оптимальных сочетаниях параметров. С данным сервисом был произведено порядка 40 экспериментов на ВР различного характера: стационарных, нестационарных, реальных, модельных. Полученные результаты (табл. 1) показали, что прогноз тренда имеет более выраженное направление, если шаг базисной функции имеет относительно большую величину (случай, когда весь временной ряд разбивается на 5-10 компонент) (рис.1, 2).

В первом случае MAPE тренда (внешняя) = 35%, во втором случае MAPE тренда (внешняя) = 12,9%. При использовании большого шага базисной функции мы хотя и добиваемся более сглаженного тренда, но одновременно и устраняем негативные всплески ВР, акцентируя тренд на наиболее общую тенденцию.

Однако при увеличении шага базисной функции ухудшаются показатели качества прогноза остатков. Их оптимальные показатели при шаге базисной функции равной 5-9 единиц.

Производится прогнозирование одной компоненты тренда, начиная с наименьшего количества точек, которые можно подать на вход программы. В эксперименте принимали участие ряды, хранящиеся в БД. Искусственные ряды также присутствовали в эксперименте.

Целью данного эксперимента является выявление ограничений, накладываемых на использование метода F -преобразований.

Для начала рассмотрим искусственный ВР, длиной 150 точек (2-12) (рис. 3)

Покажем зависимость точности прогноза от количества точек ВР, участвующих в обучении (рис. 4)

Таблица 1. Сводные данные по оценкам прогноза тренда ВР

ВР (код)	Длина ВР	Шаг базисной функци и	Метод	Тренд
				Mape (внеш)	Smape(внеш)
2-6	40	11	НС	4,95	5
2-8	43	13	НС	9,68	9,84
2-9	42	7	СЛУ	2,3	2,3
2-10	90	11	СЛУ	5,99	5,82
2-11	57	9	НС	65,67	49,44
2-12	150	5	СЛУ	0,85	0,84
2-13	25	11	СЛУ	2,04	2,02
3-15	13	5	НС	94,99	180,94
3-16	13	5	НС	1.69	1.68
3-17	13	5	СЛУ	81,27	57,78
3-24	12	5	НС	19.72	21.88
3-25	12	5	НС	84.09	145.09

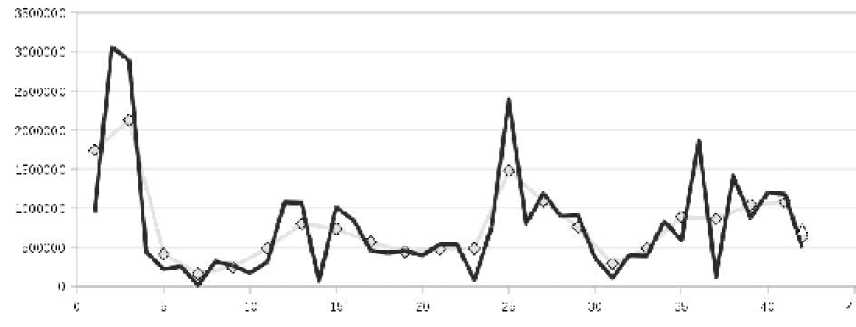
Рис. 1. Тренд построен при малом шаге базисной функции

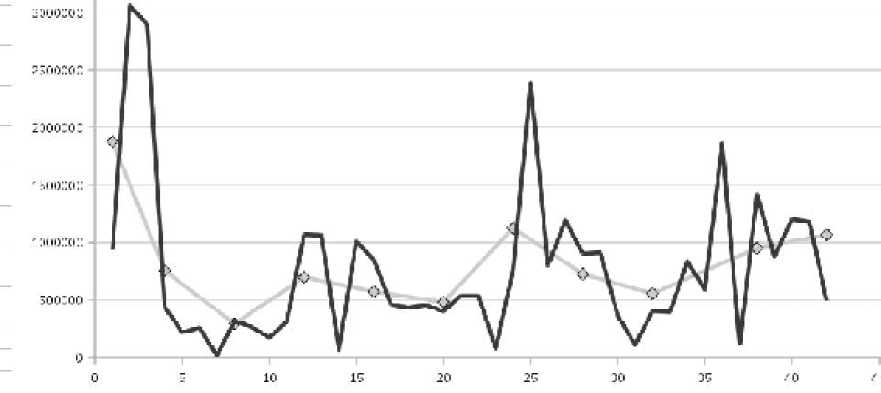
Рис. 2. Тренд построен при большом шаге базисной функции

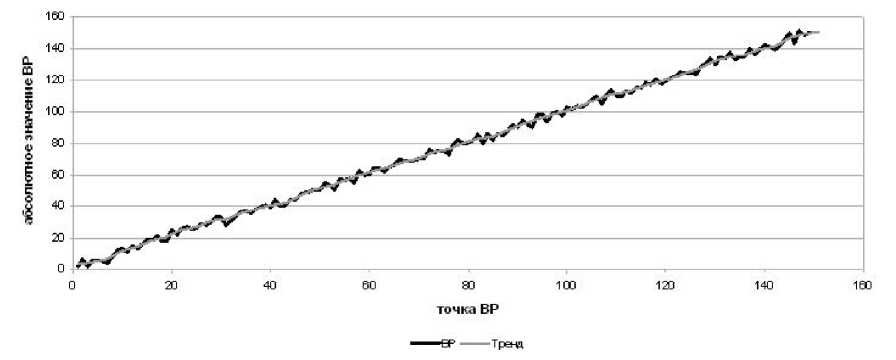
Рис. 3. ВР и построенный на нем тренд

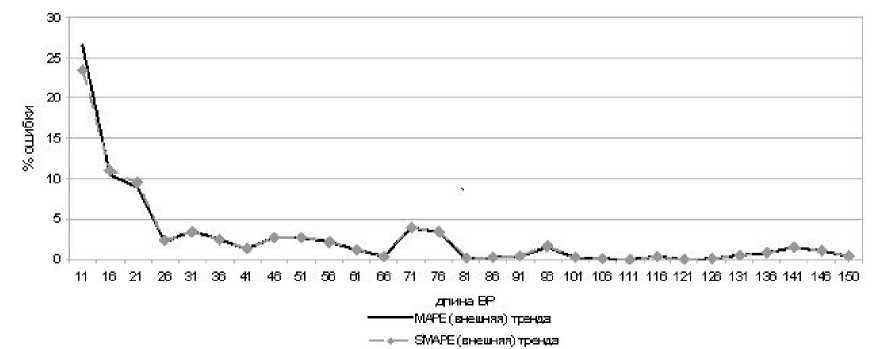
Рис. 4. Зависимость % ошибок от длины тренда

На рисунке показаны критерии оценки: MAPE (внешняя) тренда и SMAPE (внешняя) тренда. По рисунку можно выделить область, когда ошибка стабилизируется. Это наступает после 26 точек ВР, используемых для обучения. Данный случай

- когда в прогнозе проявляется линейность тренда, участвующего в обучении. На графиках ошибок также (за редким исключением) проявляется линейная зависимость: чем больше длина ВР для обучения — тем точнее прогноз.

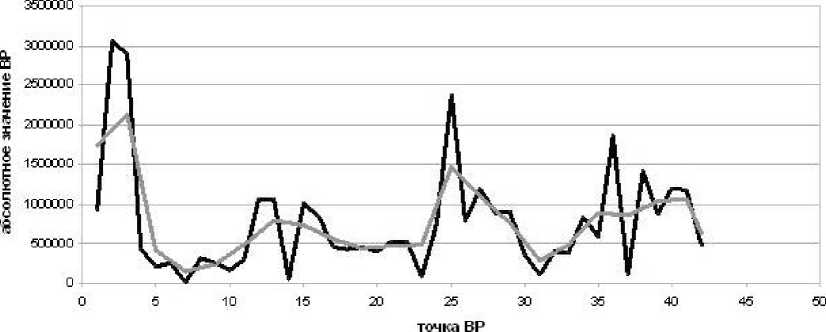
ВР Тренд

Рис. 5. ВР и построенный на нем тренд

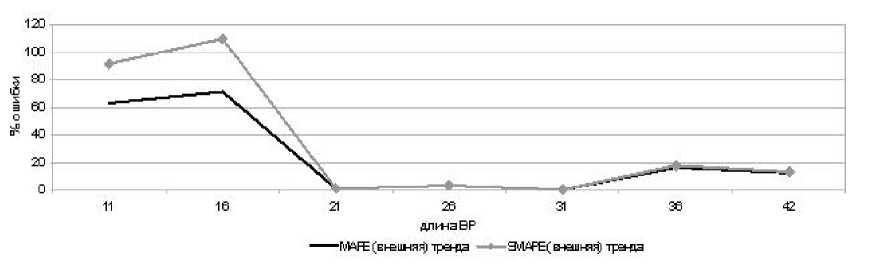
Рис. 6. Зависимость % ошибок от длины тренда

Теперь рассмотрим реальный ВР, длиной 43 точки (2-8) (рис. 5).

И также построим зависимость показателей качества прогноза от длины ВР (рис. 6)

На данном графике также видна тенденция, когда показатели качества входят в допустимую зону в районе 21-26 точек ВР. Как показано в сводной таблице на данном ВР достигнутая точ- ность MAPE (внешняя) тренда ? 10% (на максимально возможном количестве точек данного ряда).

Рассмотрим ряд с выраженным трендом, но имеющим нестационарности (реальный ВР) длиной 42 точки (2-9) (рис. 7, 8)

Видно, что ошибка практически не изменятся от длины ряда (за счет выраженного тренда)

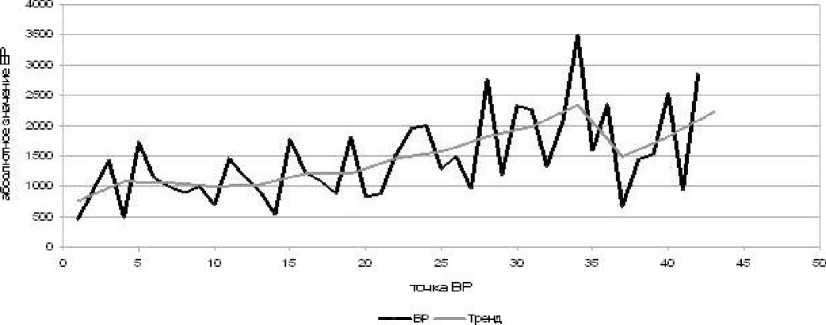
Рис. 7. ВР и построенный на нем тренд

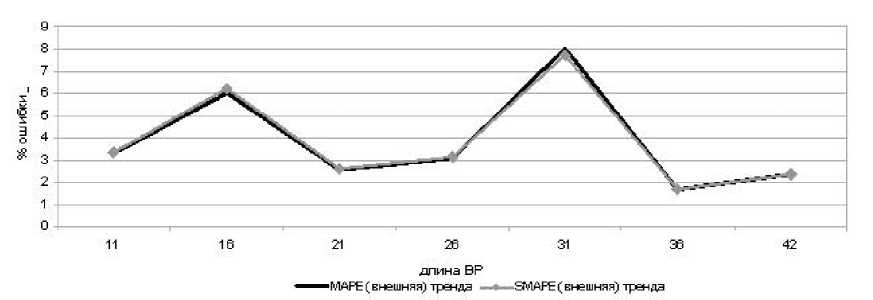
Рис. 8. Зависимость % ошибок от длины тренда

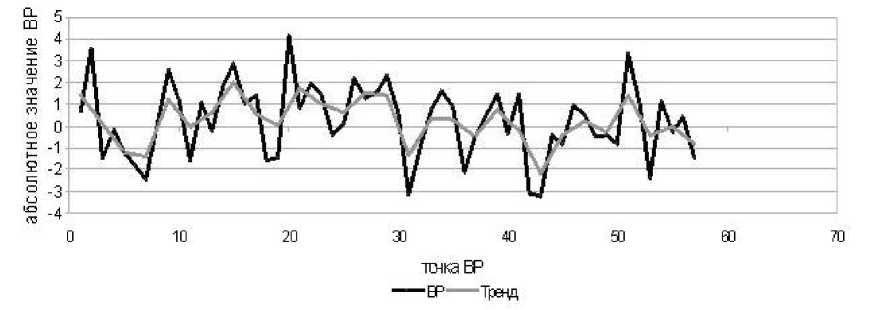
Рис. 9. ВР и построенный на нем тренд

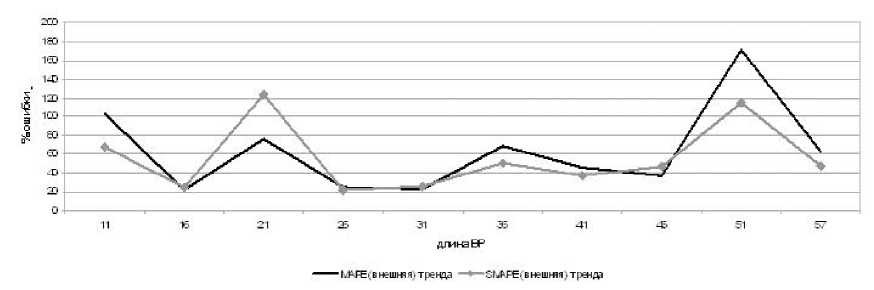
Рис. 10. Зависимость % ошибок от длины тренда

и имеет небольшую величину (до 10%) - линейность тренда. Только при переходе через излом тренда ошибка немного повышается — за счет того, что разность прогноза при обучении и реальной величины тренда имеет большую величину, чем на всем остальном ВР.

Ряд, без выраженного тренда длиной 57 точек (2-11) (рис. 9. 10):

Ошибка на таком ВР очень высока, и не зависит от длины ряда, участвующего в обучении. В такой ситуации снизить ошибку можно за счет сглаживания тренда — увеличения шага базисной функции. Но, полагаю, что такой шаг не име- ет практической ценности, поскольку происходит вырождение тренда в прямую и теряется суть прогноза тренда — выявления тенденции.

Проведенные эксперименты показали, что данный метод достаточно хорошо работает (% ошибок укладывается допустимый интервал < 20%) на рядах с выраженным трендом и лишенных случайных перепадов значений. Заданная точность достигается уже при длине ВР более 25-30 точек. Вследствие этого необходимо дополнить использование данного метода способом определения характера ВР для предварительного анализа и принятия решения о целесообразности прогноза.

Исследование выполнено при поддержке