Применение метода F-преобразования для прогноза тренда и числового представления временного ряда

Метод F-преобразования. Нечеткое сглаживание временных рядов на основе нечеткого преобразования (F-преобразования) – методика, разработанная И. Перфильевой [1], которая может быть отнесена к методикам нечеткого приближения. F-преобразование представлено для непрерывных функций и функций на ограниченном наборе точек. Оно предполагает задание нечеткого разбиения универсального множества. В качестве последнего выбирается конечный интервал [a,b] действительной прямой. Зафиксируем n (n>2) узлов x1,…,xn на [a,b] и предположим, что x1 ^... ^ xn, причем a=x1, b=xn. Под нечетким разбиением    [a,b]    будем    понимать совокупность n функций A1,…,An: [a,b]→[0,1], удовлетворяющих следующим свойствам: 1. Ak: [a,b] →[0,1],Ak(xk) = 1

• 2.  A k (x)=0  если x t ( x_k - 1 , x_{k +1}) , где для

• 3.    A k (x) непрерывна

• 4.    A k (x), k=2,…,n строго возрастает на [ x k-1 ,x k ] и строго убывает на [ x k ,x k+1 ].

• 5.   S ^Ak^(x) = ¹ для всех x ^{g [} a , b ^]

единообразия обозначения мы положим x 0 = a , x_n+ 1 = b

Функции A 1 ,…, A n называются базисными функциями. Базисные функции могут служить также функциями принадлежности нечетких подмножеств A 1 ,…, A n (обозначения функций и множеств унифицированы). Отметим, что форма базисных функций может быть уточнена дополнительно и согласована с такими требованиями к модели, как, например, гладкость. Следующие формулы представляют нечеткое разбиение отрезка [x 1 ,x n ], полученное совокупностью функций:

A i^{( x} ) = '

1   ( x - x )     _r     .

1--—-, x g [ x i , x ₂]

h i

0, иначе

( x - x ,)      _r        .

—---k-,x E [xk-i,xk], hk-1

A k ⁽ x ) = *

A 1^{( x} ) = ‘

.   ( x - x_k )     _r

1--;------,x G [xk, xk+1], hk

0, иначе

1 -

^{( x - x}n - 1 )

h

n - 1

0, иначе

, ^{x g [ x}n - 1 , ^xn ^]

где k =1,…, n – 1 и h k = x k+1 – x k .

Предположим, что функция f имеет своей областью      определения      множество

P = ^{А,-., pi } ^{c [} a , b ^] , где l> n . Множество P считается плотным относительно нечеткого разбиения A 1 ,…, A n , если выполнено условие:

( V k )( V j ) A k ( P j ) >  0

Пусть   Ak(pj)=akj,k=1,…,n;   j=1,…,l,   тогда матрица Anxl = akj называется матрицей нечеткого разбиения для P, для которой справедливы свойства:

• 1.   ( V k )( V j ) a „ .e [0,1]

• 2.   ( V i ) S k = 1 a„ = 1

F-преобразованием вектора f , определяемым матрицей нечеткого разбиения A , назовем вектор F n [ f ], где

l

F =    j = 1 i f

F. [ f ] = ( F i ...F . ) и '    £ i = 1 a ,

и прогноз вектора остатков:

R k + i = a R k + e R k - I-

Координаты вектора  Fn[f]  назовем компонентами F-преобразования. Обозначим ai = £ H a,, i =1,-.-,n;                     тогда

(aiF,.-.,anFn)T = A * f . Компоненты F-преобразования являются точками минимума функции, задающей критерий взвешенного среднеквадратичного отклонения. Пусть Fn[f] есть F-преобразование f, определяемое Anxl = akj Обратным F-преобразованием Fn[f] назовем вектор  fF,n,  вычисляемый по формуле fF, n = Fn [ f ] * A. Можно доказать, что если n возрастает, тогда fF,n(pj) сходится f(pj),j=1,…,N. F-преобразование имеет (кроме прочих) следующие свойства, важные для использования в качестве сглаживания временных рядов: a) у него прекрасные фильтрующие свойства; b) его легко вычислять c) F-преобразование стабильно относительно выбора точек p1,…,pN. Это означает, что при выборе других точек pk (и, возможно, изменяя их число N), результирующая функция fF,n значительно не меняется.

Реализация метода F-преобразования. Прогноз. Сглаживание методом F-преобразования было реализовано в сервисе прогнозирования компоненты тренда и числового представления временного ряда. Данный сервис работает в составе Internet-сервиса, интегрирующего нечеткое моделирование и анализ нечетких тенденций временных рядов. В качестве сглаживаемой функции выступает временной ряд. Сглаживание производится по формуле (1). Полученные компоненты представляют собой тренд временного ряда. Прогнозирование тренда и прогнозирование числового представления временного ряда производится раздельно. Для этого необходимо вычислить так называемые остатки – разность между временным рядом и его трендом:

R = (№,) — F k ) } rde j : A„(J)> 0

Полученный вектор R -вектор остатков для k -й компоненты тренда. Прогноз тренда и векторов остатков реализуется по формуле линейной комбинации. Прогноз компоненты тренда:

F_k + i = a F_k + 3 F_k — 1 ...

Для получения прогноза находится решение системы уравнений:

J F k - i = aF k — 2 + eF k - 3

I F k = ^aFk - 1 + ^e F k - 2 •

Аналогично строится прогноз вектора остатков. Также для построения прогноза используется нейронная сеть. Реализовано два вида нейронных сетей:   многослойный перцептрон и сеть Кохонена с выходной звездой Гроссберга. Вид нейронной сети определяет вид входных данных: на вход многослойного перцептрона подаются только абсолютные значения (Fk,Fk-1,…), на вход сети Кохонена подаются значения точек тренда, вычисленные относительно друг друга (Fk – Fk-1, Fk-1 – Fk-2).

В ходе проведения экспериментов выяснилось, что процесс получения прогноза тренда и остатков зависит от некоторых параметров, которые в модели не удается задать жестко. Выбор данных параметров в значительной степени влияет на качество прогноза. Определим их:

• •   степень авторегресии при построении

прогноза тренда (область значений [1,5] )

• •    метод, которым производится прогноз (значения:   [line, neyro,   neyro_with_delta,

neyro_delta]) Расшифровка методов:

line — решение системы линейных уравнений neyro - нейронная сеть, на вход – абсолютные значения предыдущих компонент neyro_delta — нейронная сеть, на вход -только разности между предыдущими компонентами neyro_with_delta — нейронная сеть, на вход – абсолютные значения предыдущих компонент, а также разности между ними

• •    количество точек, покрываемых базисной функцией (значения [5, 7, 9, 11, 13]);

• •    сезонность (история отстоит на k точек от прогноза).

Сочетание параметров, при котором получается наилучший прогноз получается перебором. Для оценки качества прогноза вычисляется критерий MAPE:

n

MAPE =

n £

Y t

*100%

где Y - реальное значение точки тренда, Y -модельное (спрогнозированное) значение точки тренда.

Также приводится оценка по критерию SMAPE:

n

SMAPE = ntt(Yt+Y/2

*100%

При его (2) минимальном значении в режиме подбора параметров делается вывод об их оптимальном сочетании.

В ходе экспериментов было установлено, что на качество прогноза влияет количество нейронов во внутреннем слое. Если первоначально количество нейронов во внутреннем слое рассчитывалось по формуле n=n +1, где n - количество нейронов входного слоя, то теперь рассчитывается так: n=n+50. Число 50 подобрано эмпирически. При дальнейшем его увеличении возрастает время обучения сети без существенного увеличения качества прогноза. После получения прогнозных значений тренда и вектора остатков возможно построение числового представления прогноза временного ряда. Для этого производится сложение прогнозной компоненты тренда и прогнозного вектора остатков.

Общие сведения о результатах экспериментов. С данным сервисом был произведен ряд экспериментов на временных рядах экономического характера. Они показали, что прогноз тренда имеет более выраженное направление, если количество точек, покрываемых одной базисной функцией, имеет относительно большую величину.

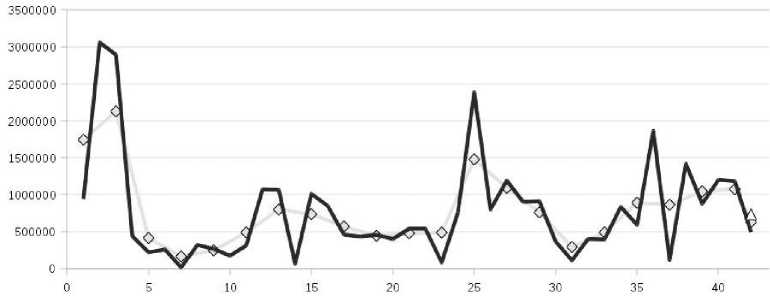
Рис. 1. Тренд построен при малом количестве точек, покрываемых базисной функцией

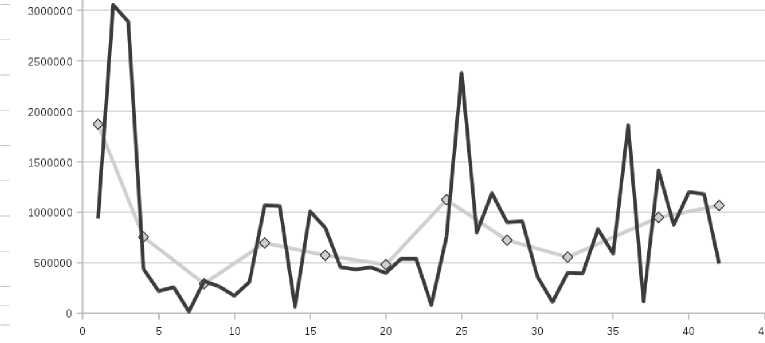
Рис. 2. Тренд построен при большом количестве точек, покрываемых базисной функцией

В первом случае MAPE тренда (внешняя) = 35%, во втором случае MAPE тренда (внешняя) = 12,9%. При использовании большого шага базисной функции мы хотя и добиваемся более сглаженного тренда, но одновременно и устраняем негативные всплески ряда, акцентируя тренд на наиболее общую тенденцию. Однако при увеличении шага базисной функции ухудшаются показатели качества прогноза остатков.

Зависимость качества прогноза от длины временного ряда. Производится прогнозирование одной компоненты тренда, начиная с наименьшего количества точек, которые можно подать на вход программы. Искусственные ряды также присутствовали в эксперименте. Целью данного эксперимента является выявление ограничений, накладываемых на использование метода F-преобразований.

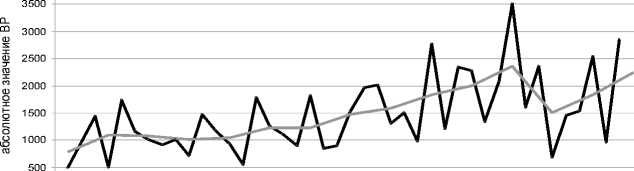
Для начала рассмотрим искусственный временной ряд, длиной 150 точек (рис. 3). Покажем зависимость точности прогноза от количества точек временного ряда, участвующих в обучении (рис. 4):

20              40              60

100             120             140

точка ВР

ВР     Тренд

Рис. 3. Ряд и построенный на нем тренд

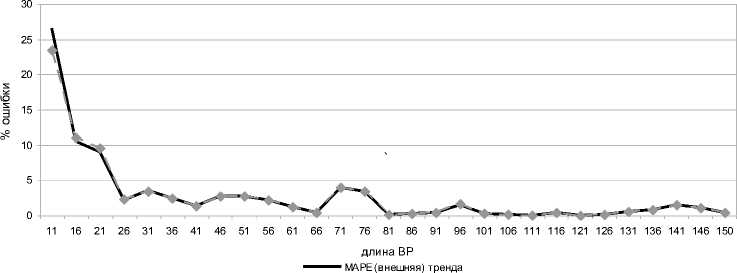
SMAPE (в нешняя) тренда

Рис. 4. Зависимость % ошибок от длины тренда

На рисунке показаны критерии оценки: MAPE (внешняя) тренда и SMAPE (внешняя) тренда. По рисунку можно выделить область, когда ошибка стабилизируется. Это наступает после 26 точек ряда, используемых для обучения. Данный случай - это когда в прогнозе проявляется линейность тренда, участвующего в обучении. На графиках ошибок также (за редким исключением) проявляется линейная зависимость: чем больше длина ряда для обучения — тем точнее прогноз. Теперь рассмотрим реальный ряд, длиной 43 точки (рис. 5) и построим зависимость показателей качества прогноза от длины ряда (рис. 6).

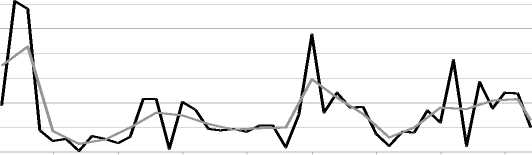
5          10         15         20         25         30         35         40

точка ВР

ВР     Тренд

Рис. 5. Ряд и построенный на нем тренд

§ 80

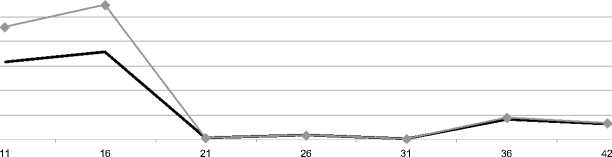
длина ВР

^^^^^^ MAPE (внешняя) тренда      SMAPE (в нешняя) тренда

Рис. 6. Зависимость % ошибок от длины тренда

На рис. 6 также видна тенденция, когда показатели качества входят в допустимую зону в районе 21-26 точек временного ряда. Как показано в сводной таблице на данном ряде достигнутая точность MAPE (внешняя) тренда ≈ 10% (на максимально возможном количестве точек данного ряда). Рассмотрим ряд с выраженным трендом, но имеющим нестацио-нарности (реальный ряд) длиной 42 точки (рис. 7) и зависимость ошибок от длины тренда (рис. 8).

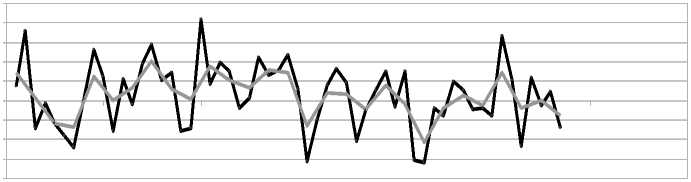
10          15

точка ВР

35         40         45         50

^^н_^^м ВР ^^^^^^н Тренд

Рис. 7. Ряд и построенный на нем тренд

31                36                42

длина ВР

^^^^^^^ MAPE (внешняя) тренда

SMAPE (внешняя) тренда

Рис. 8. Зависимость % ошибок от длины тренда

Видно, что ошибка практически не изменятся от длины ряда (за счет выраженного тренда) и имеет небольшую величину (до 10%) - линейность тренда. Только при переходе через излом тренда ошибка немного повышается – за счет того, что разность прогноза при обучении и реальной величины тренда имеет большую величину, чем на всем остальном ряде.

Построим ряд без выраженного тренда длиной 57 точек (рис.9) и зависимость ошибок от длины тренда (рис. 10). Ошибка на таком ряде очень высока, и не зависит от длины ряда, участвующего в обучении. В такой ситуации снизить ошибку можно за счет сглаживания тренда – увеличения шага базисной функции. Но, полагаю, что такой шаг не имеет практической ценности, поскольку происходит вырождение тренда в прямую и теряется суть прогноза тренда – выявление тенденции.

О) т го о о

0m

§ го

-2

-3

-4

точка ВР

^ж^м ВР ^^^^н Тренд

Рис. 9. Ряд и построенный на нем тренд

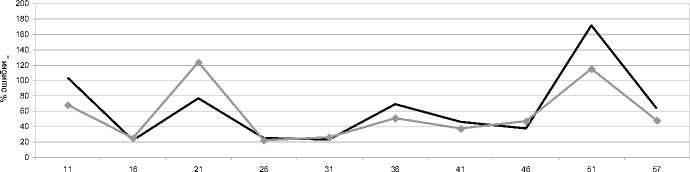
длина ВР

^^^^■1 MAPE (внешняя) тренда е SMAPE (внешняя) тренда

Рис. 10. Зависимость % ошибок от длины тренда

Генетическая оптимизация. Как описывалось ранее, имеется ряд параметров, значения которых не могут быть определены однозначно до запуска сервиса. Оптимальное решение может быть найдено путем перебора всех значений параметров. Задачи такого типа с меньшими затратами могут быть решены путем применения эволюционных алгоритмов. Предлагается следующий классический алгоритм генетической оптимизации:

Имеется функция F ( x 1, …, x 4) – оценка критерия MAPE построения прогноза тренда (должна быть минимизирована), где:

x 1 – степень авторегресии при построении прогноза тренда (целочисленная область значений [1,5]);

x 2 – метод, которым производится прогноз (значения: [line, neyro, neyro_with_delta, neyro_delta])

x 3 – количество точек, покрываемых базисной функцией (целочисленные значения [5, 7, 9, 11, 13])

x 4 – прогноз изначально строился на основании истории из предыдущих N точек. Для выявления сезонности следует строить прогноз, отодвигая историю на t точек назад: F k = αF k-t + βF k-t-1 + …

Алгоритм:

• •    Хромосомы имеют битовое представление (кодируем в коде Грея для получения отличия соседних хромосом в 1 бите).

Вначале производится нормировка значений параметров к интервалу [0, 1]

• •    Оператор скрещивания (возможен случайный выбор между данными вариантами оператора скрещивания)

• •    Сформировать случайно начальную популяцию B0 = {A1,A2,…,Ak) состоящую из k особей ( k определить эмпирически)

• •    Вычислить приспособленность каждой особи FAi = fit(Ai) , i=1…k

• •    Выбрать двух особей Ac из популяции. Ac = Get(Bt).

• •    Произвести скрещивание (выбрав один из предложенных вариантов) и получить новую особь.

• •    Произвести мутацию генов с некоторой вероятностью

• •    Оценить полученную особь функцией приспособленности и добавить в популяцию взамен худшего родителя (т.о. сохраняется количество особей популяции)

• •    Выполнить пункты 5-8 m раз

• •    увеличить счетчик эпох

• •    проверить условие останова (предельное количество эпох или предельное количество особей одного генотипа в популяции).

Выводы: проведенные эксперименты показали, что данный метод достаточно хорошо работает (% ошибок укладывается допустимый интервал <20%) на рядах с выраженным трендом и лишенных случайных перепадов значений. Заданная точность достигается уже при длине временного ряда более 25-30 точек. Для этого необходимо дополнить использование данного метода способом определения характера ряда для предварительного анализа и принятия решения о целесообразности прогноза. После проведения экспериментов по временным рядам (их количество равно 111) средняя ошибка прогноза MAPE (тренда) составила 16,9%.