Применение метода главных компонент для исследования крупномасштабных вихревых структур в турбулентном слое смешения

Результаты PIV измерений обладают большой информативностью благодаря своей па-норамности. Главное преимущество перед зондовыми методами - это возможность анализа, пространственных когерентных структур. Однако при попытке исследования с помощью PIV метода, крупномасштабных структур в развитом турбулентном течении возникает проблема. их выделения на. фоне мелкомасштабной завихренности. Для решения подобных проблем уже довольно давно и успешно применяется метод главных компонент, так же известный, как разложение Карунена-Лоэва, собственное ортогональное разложение или преобразование Хотеллинга. Идея метода, была, предложена. J.L. Lumley в 1967 году [1] как способ выделения крупномасштабных когерентных структур на фоне мелкомасштабных случайных флуктуаций. В дальнейшем метод был развит L. Sirovich и предложен метод снепшотов (англ, method of snapshots) [2]. Этот вариант POD применяется при обработке экспериментальных данных, в частности данных PIV, и результатов численного моделирования. Суть метода, состоит в нахождении в пространстве данных подпространств меньшей размерности, в ортогональной проекции на. которые дисперсия максимальна. В ходе разложения определяется оптимальный (в смысле максимизации дисперсии) базис. При помощи

такого базиса можно описать основные (в смысле энергии) параметры турбулентного течения, используя малое количество базисных векторов (мод). Разложение часто применяется для исключения вклада низкоэнергетических флуктуаций. Так как моды отсортированы по их вкладу в общую энергию, крупномасштабные структуры в течении представляются небольшим количеством первых главных компонент. Также эти структуры представляют анизотропные геометрические параметры течения. Моды, соответствующие низкоэнергичным структурам, описывают изотропную турбулентность. С целью выделения когерентных структур в турбулентном течении метод главных компонент по большей части использовался в зарубежных работах. Было рассмотрено применение метода главных компонент для исследования инвариантов тензора анизотропии турбулентного течения [3]. В работе K.S. Ball, L. Sirovich [4] проведен анализ собственных функций разложения по методу главных компонент данных численного моделирования турбулентного потока в канале.

В данной работе метод главных компонент использовался для выделения крупномасштабных когерентных вихревых структур в слое смешения струи аэродинамической трубы с открытой рабочей частью. Поля скорости измерялись с помощью PIV системы. Работа выполнена в рамках задачи исследования воздействия на слой смешения вихрегенераторов, установленных на срезе сопла.

2.    Метод главных компонент

Строгое описание метода главных компонент можно найти в работах [1], [2]. Рассмотрим работу метода на двумерном примере. Для этого генерируем центрированную выборку из 100 случайных векторов X г (ж1 ,ж₂), между компонентам и которых есть связь ж₂ = 2 • ж1 + е, где е — нормально распределенная случайная величина с матожиданием ц = 0 и средне-

Задача состоит в определении новой системы координат, которая удовлетворяет следующим требованиям:

• 1)    Выборочая дисперсия вдоль первой координаты максимальна (её называют первой главной компонентой).

• 2)    Выборочная дисперсия вдоль второй координаты максимальна, при условии ортогональности первой координате.

• 3)    Выборочная дисперсия к-й координаты максимальна, при условии ортогональности к — 1 первой координате.

Найдем такую систему координат. Рассмотрим единичный вектор v и найдем дисперсию проекции данных на него. Длина проекции вектора X і нa v равна (v^T • X^. Учитывая, что v ^T X і — тоже центрированная величина, дисперсию проекции можно записать как

D [vTX,] = М [(vTX,) • (vTX,)T] = М ДX,XTv] = vTM [X,XT] v = vTSv, где M [... ] — математическое ожидание, S — ковариационная матрица выборки. Таким образом, выборочная дисперсия максимизируется, когда максимально vTSv. При помощи отношения Релея

R( x , А ) =

х^т • А • х х^т • х

для случая ковариационной матрицы можно показать, что R( x , S ) достигает максимального значения Amax в случае, когда х = v _max, г де A_max и v _max — наибольшее собственное число и соответствующий ему собственный вектор ковариационной матрицы У. Ковариационная матрица симметрична и вещественна, следовательно, имеет неотрицательные собственные числа и ортогональные (или приводимые к ним) собственные векторы. Таким образом, базис из собственных векторов ковариационной матрицы задает искомую систему координат. Заметим, что собственные значения ковариационной матрицы равны выборочным дисперсиям вдоль соответствующих направлений.

Для получения искомых направлений необходимо подсчитать ковариационную матрицу и найти её собственные значения и собственные векторы. Вычислим ковариационную матрицу для генерированной выборки:

S=f

’833,25 1607,5 1607,5 3230,7 .

Её собственные числа Аі, А2 и собственные векторы vi, v2 будут следующими:

Ах = 4037,2; А2 = 26,7, vi =

Г0,4484          -0,8938

[0,8938] ^{; v}2 = [ 0,4484 ] ^.

Нанесем на график полученные собственные векторы, умноженные на 2VA, т.е. длиной в два стандартных отклонения вдоль соответствующего направления (рис. 2а). Судя по собственным числам, первой главной компонентой будет ось vi. Спроецировав данные на это направление (рис. 26), можно избавиться от составляющей с меньшей дисперсией. На рис. 26 хорошо видна изначально заданная зависимость Х2 = 2ті.

Эту процедуру можно представить и по-другому: так как базис из собственных векторов ковариационной матрицы ортогонален, экспериментальные точки можно получить при помощи линейной комбинации базисных векторов. Для определения коэффициентов необходимо перейти в систему координат из собственных векторов ковариационной матрицы, составив матрицу перехода.

Удобным инструментом для применения метода является сингулярное разложение (SVD, singular value decomposition). Сингулярное разложение — это представление матрицы в виде произведения трех матриц особого вида. Пусть М — матриц а размера m х п, тогда она представляется при помощи SVD следующим образом:

М = ULV *, где L — матрица размером m х п, на главной диагонали которой стоят сингулярные числа, остальные её элементы равны нулю, U(m х m) и V(п х п) — левая и правая сингулярные матрицы, V* — сопряженно-транспонированная матрица к V (в случае вещественных матриц эквивалентно транспонированию). Опустив математические выкладки (связь метода главных компонент и SVD рассмотрена, например, в [5], [6]), отметим, что матрицы U и Vт состоят из собственных векторов матриц М • Мт и Мт • М соответственно. Учитывая, что S = І (М • Мт), матрица U состоит из собственных векторов ковариационной матрицы для М, а столбцы матрицы М представляются как линейные комбинации этих векторов. Если обнулить некоторое сингулярное число в L, соответствующий ему собственный вектор будет исключен из произведения ULVт. Следовательно, чтобы применить метод главных компонент при помощи SVD, нужно разложить матрицу X = ULVт. В зависимости от задачи определяются компоненты, от которых неообходимо избавиться (обычно это направления с наименьшей дисперсией). Сингулярные числа в L, соответствующие этим направлениям, необходимо обнулить и посчитать новое значение ULVт = X', где X ‘ — новая матрица, в которой содержатся спроецированные на несколько главных компонент данные. Сингулярные числа и собственные значения ковариационной матрицы связаны соотношением

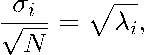
где Ог — сингулярное число, А, — собственное значение, N — количество точек. Количество ненулевых сингулярных чисел, как и ненулевых собственных чисел ковариационной матрицы, равно рангу матрицы входных данных.

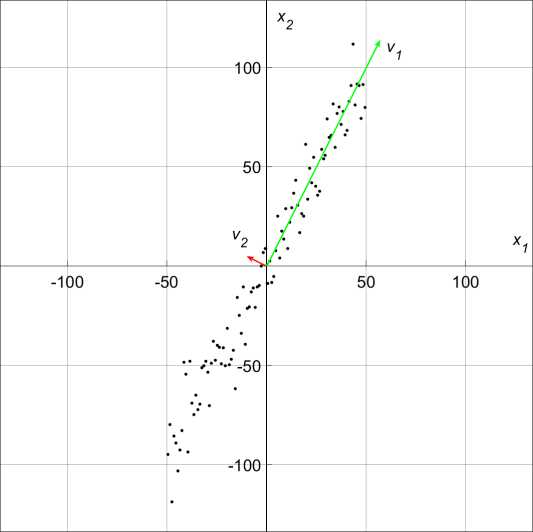
а)

Рис. 2. Собственные вектора ковариационной матрицы (а) и проекция данных на первую главную компоненту (б)

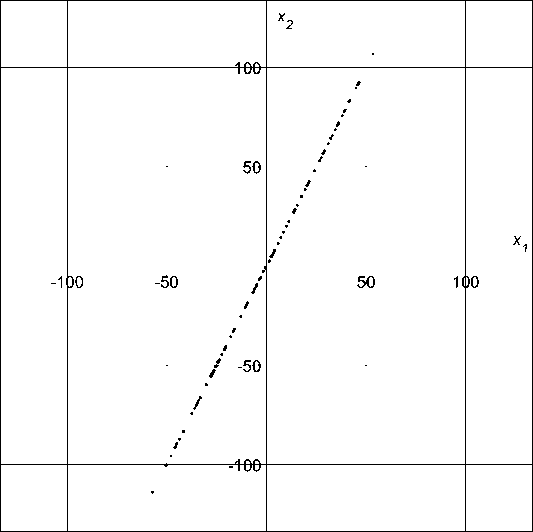
б)

В итоге при помощи метода главных компонент был найден ортогональный базис и вклад в общую дисперсию для каждого из направлений. При помощи представления данных в таком базисе, можно исключить из рассмотрения составляющие с меньшим вкладом в суммарную дисперсию, применив, таким образом, метод главных компонент как фильтр.

Метод часто применяется к измерениям в пространстве большой размерности, к каким относятся и PIV измерения (каждое поле можно рассматривать как точку в пространстве размерностью a • 5. где а и 5 — размеры поля). Применительно к турбулентному течению, полученные моды представляют наиболее энергоемкие структуры в течении.

3.    Результаты обработки

Частью работы по изучению влияния вихрегенераторов на характеристики пограничного слоя струи было экспериментальное исследование поля течения при помощи PIV на установке Т-03 ЦАГИ. Принципиальная схема установки представлена на рис. 3.

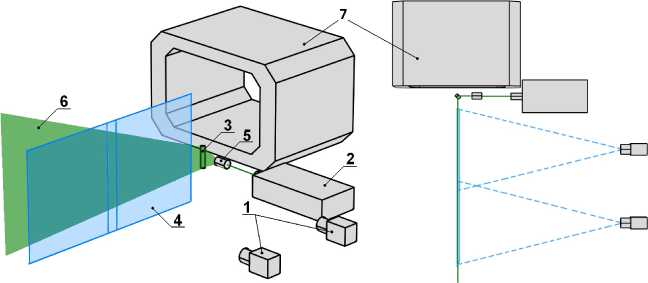
Рис. 3. Принципиальная схема экспериментальной установки. Цифрами на рисунке обозначены: 1 — цифровые камеры, 2 — двойной импульсный лазер, 3 — зеркало, 4 — поле зрения камер, 5 — оптическая система для фокусировки и создния световой плоскости, 6 — световая слоскость, 7 — сопло АДТ

Регистрация и обработка изображений проводилась при помощи системы PIV «Полис». Источником освещения служил двойной импульсный твердотельный лазер. В качестве средств регистрации использовались две камеры «Видеоскан 4021» разрешением 2048 х 2048 пикселей с 60-миллиметровыми объективами. Генератор дыма располагался на полу рабочей части трубы так, что дым всасывался потоком в диффузор и возвращался в рабочую часть, проходя весь тракт трубы, что обеспечивало равномерность засева потока частицами.

Измерения проводились сериями приблизительно по 500 пар кадров. Были использованы две камеры для увеличения общего поля зрения. После обработки к полученным полям размерами 126 х 63 применялась маска для исключения из рассмотрения плохо подсвеченных областей с большим количеством ошибочных векторов. Пример полученного поля скорости представлен на рис. 4. Для простоты дальнейшей обработки было вычислено среднее по времени поле скорости, и дальнейшая работа велась с отклонением от среднего. Без доплнительной обработки в полученных полях скорости не удалось выделить каких-либо структур, поэтому была предпринята попытка применить метод главных компонент.

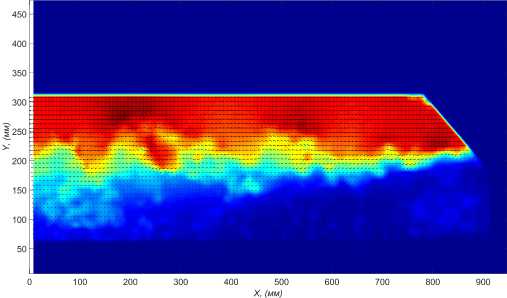
Рис. 4. Пример поля скорости в слое смешения. Направление потока справа налево

Для применения метода главных компонент представим полученные данные в виде «матриц снепшотов» (англ, «snapshot data matrix») вида

Vx(x1 , t1)   . .. Vx(x1 ,t_N1 )

e ^^MxNt

• •                                  ••

• •                                      ••

• •                                          ••

Vx(xM ,ti ) . .. Vx(xM ,tNt )

где Уж — продольная компонента скорости, М — количество точек на поле скорости, N — количество полей. Каждый столбец такой матрицы — поле скорости, представленное в виде вектор-столбца. Таким образом, экспериментальные данные представляются в виде Nt точек в М-мерном пространстве. Аналогичная матрица составляется для поперечной компоненты скорости Vy.

Для применения метода главных компонент найдем ковариационную матрицу, её собственные числа и собственные векторы и отсортируем их по убыванию собственных чисел. Рассмотрим полученные собственные числа. Для этого построим график, по оси абсцисс которого будет отложен номер числа п, а по оси ординат — собственные числа, нормированные на их сумму: A_n /S, где S = ^^ 1 Х_п. Так как собственные числа равны дисперсиям вдоль соответствующих направлений, сумма собственных чисел равна полной дисперсии. Следовательно, точки на графике показывают долю дисперии (и энергии), приходящуюся на соответствующую моду. Графики представлены на рис. 5а, б). Чтобы определить, какую долю энергии описывают первые п мод, необходимо сложить первые п собственных чисел.

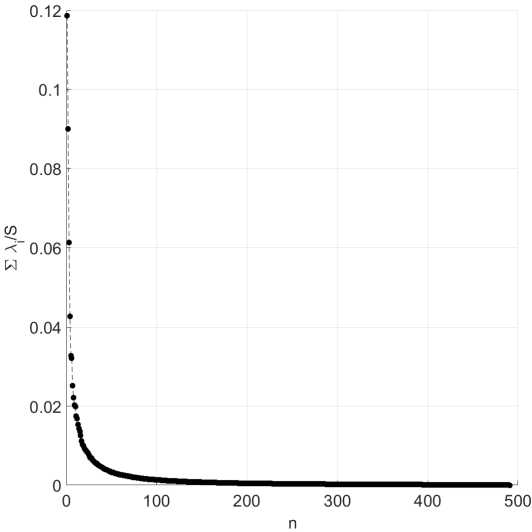
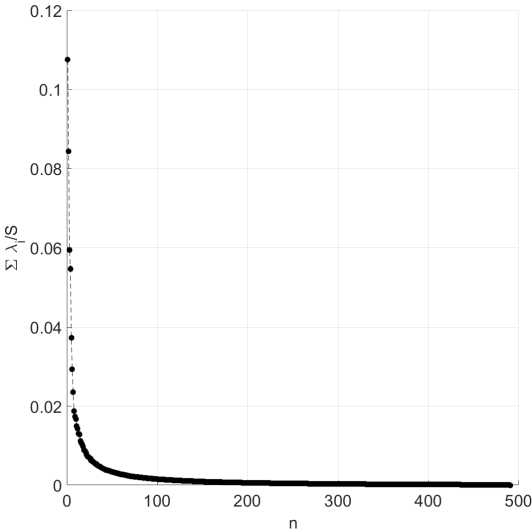
а)                                                       б)

Рис. 5. Нормированные собственные числа для Уж (а), и Vy (б)

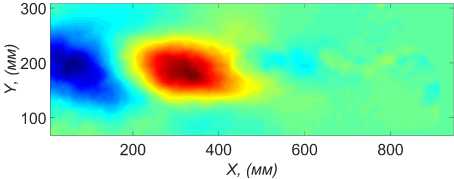
На рис. 6-7 представлены первые две моды продольной и поперечной составляющей скорости (сответствеющие первым двум наибольшим собственным числам). Области под маской на рисунках не показаны. Видно, что моды содержат в себе периодические структуры. Поля скорости могут быть восстановлены с заданной точностью при помощи линейной комбинации некоторого количества таких мод.

Теперь необходимо «собрать» поля скорости, используя лишь несколько первых главных компонент. Их количество выбиралось опытным путем с помощью собственных чисел. Были рассмотрены несколько вариантов, два из которых представлены на рис. 8, 9. При увеличении количества используемых компонент учитываются все более мелкие структуры в течении. Для дальнейшей обработки было решено использовать четыре первые моды (рис. 8), что описывает примерно 0,3 от всей энергии пульсаций.

На полученном поле четко видны периодические структуры. По полям скорости были вычислены поля завихренности, к которым была применена процедура сглаживания (пример такого поля представлен на рис. 10а). Анализ полей завихренности позволил сделать вывод о структуре течения: наиболее энергоемкие вихри, появляющиеся в слое смешения, в ходе движения отдаляются друг от друга, деформируются и начинают сливаться (рис. 106). Явление слияния вихрей в пограничном слое уже наблюдалось, и описано например, в [7].

а)                                                      б)

а)

Рис. 7. Вторая мода числа для Vx (а), и Vy (б)

Рис. 6. Первая мода для V x (а), и V у (б)

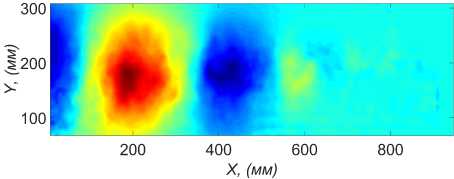
б)

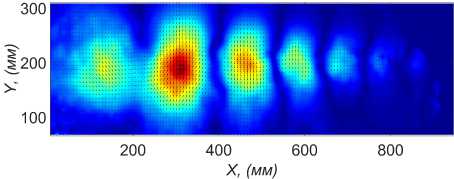
Рис. 8. Поле скорости после фильтрации с использованием первых 4 главных компонент

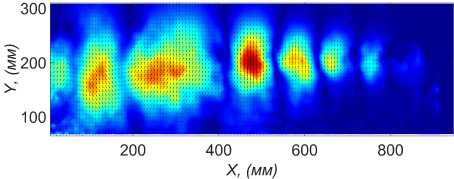
Рис. 9. Поле скорости после фильтрации с использованием первых 10 главных компонент

Для оценки влияния вихрегенераторов были проведены измерения с вихрегенераторами и без них. Каждая серия была обработана при помощи метода главных компонент. Чтобы определить, какую долю энергии описывают первые п мод, необходимо сложить первые п собственных чисел, поэтому удобно рассмотреть график зависимости суммы первых п нормированных на S собственных чисел в зависимости от п, т.е. ^ ^Г=1 ^* На рис. 11 представлены такие графики для измерений с одной из конфигураций вихрегенераторов и без них. По графикам можно сказать, что установка вихрегенераторов уменьшает долю энергии, приходящуюся на крупномасштабные структуры.

4.    Заключение

Метод главных компонент — способ нахождения в некотором пространстве подпространств меньшей размерности, дисперсия проекции данных на которое максимальна. Применительно к изучению турбулентных течений, метод позволяет выделить в потоке когерентные структуры на фоне мелкомасштабной турбулентности, используя серию полей скорости (данные PIV или численного моделирования). Крупные когерентные структуры, которые переносят большую часть энергии потока, описываются несколькими первыми модами. Часто именно они представляют наиболее важные свойства потока. Была показана применимость метода для исследования влияния турбулизирующих устройств на срезе сопла на пульсации в слое смешения.

а)                                                      б)

Рис. 10. Два примера сглаженных полей завихренности

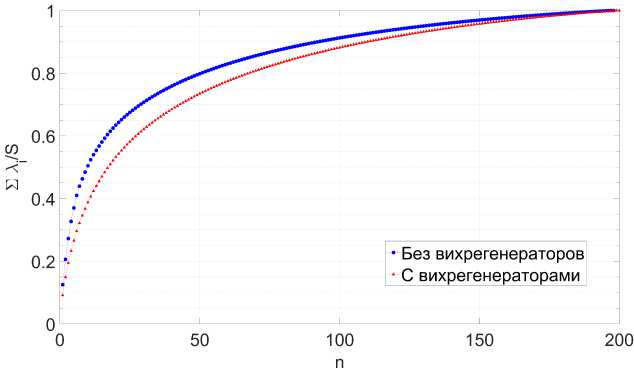
Рис. 11. Сумма первых п нормированных собственных чисел в зависимости от п для двух экспериментов