Применение метода инвариантных эллипсоидов для решения линейной задачи слежения

Целью работы является исследование задачи управления регулируемым выходом линейной системы в одной из разнообразных постановок задачи слежения (см., например, [1-3]), одна, из первых постановок этой задачи восходит к Р. Калману [4].

В работе рассматривается задача, слежения в линейной системе управления. Цель управления (которое ищется в виде статической линейной обратной связи) состоит в том, чтобы регулируемый выход системы был как можно «ближе» (в некотором смысле) к сигналу, подаваемому на. вход системы.

Предлагаемый подход к решению задачи основан на. методе инвариантных эллипсоидов [5]; в качестве технического средства, используется техника, линейных матричных неравенств (Linear Matrix Inequalities, LMI) [6]. Такой подход позволил переформулировать исходную задачу к поиску минимального ограничивающего эллипсоида, содержащего выход рассматриваемой системы. В качестве критерия минимальности в работе выбран критерий следа, соответствующий минимизации суммы квадратов полуосей эллипсоида.

С технической точки зрения проблема, сводится к решению задачи полуопределенного программирования (Semi-Definite Programming, SDP) и одномерной оптимизации [7]. Для ее решения существуют эффективные программные средства, в частности — свободно распространяемые пакеты SeDuMi и YALMIP на. базе системы Matlab.

Эффективность метода продемонстрирована на примере управления двухмассовой системой [8].

2.    Задача анализа

Рассмотрим линейную непрерывную динамическую систему х = Ах + Df (t), х(0) = хо, г = f (t) - Сх, где А Е Rnxn, С Е R/xn, D Е Rnx/, x(t) Е Rn — фазовое состояние системы, г(t) Е Rz — выход системы. Пусть матрица А устойчива, а сигнал f (t) Е R' удовлетворяет условию f = Aof + Dow,                                (1)

где Ао Е R/x/, Do Е Rixm, a w(t) Е Rm — внешнее возмущение, удовлетворяющее ограни чению

IIw(t) ^ 6 1 V t >  0.

Матрицу Ао будем предполагать устойчивой (гурвицевой). Рассмотрим расширенную систему х = Ах + Df , f = Ао f + Dow,                                (3)

г = f — Сх.

Введя в рассмотрение составной вектор

9 =

(е Rn+/,

представим систему в матричной форме:

9=(а АО)9AD)r ⏟  ⏞⏟⏞

• -—•-—•

  
  

AD г = (—С I) 9.

Нам понадобятся следующие определения.

Определение 1. Эллипсоид с центром в начале координат

8х = {х е Rn:   хтР-1х 6 1},     Р > 0,(5)

называется инвариантным для динамической системы х = Ах + Dw, если из условия х(0) е 8_Х следует х(t) е 8_Х для всех моментов времени t >  0. Это означает, что фазовое состояние системы будет всегда находиться в 8_Х, если оно находится в этом эллипсоиде в начальный момент времени.

В дальнейшем все матричные неравенства понимаются в смысле знакоопределенности матриц.

Определение 2. Эллипсоид с центром в начале координат

• 8,    = {г е R^z:   г^т (СРС^Т)^-1г 6 1},     Р > 0,

называется ограничивающим по выходу для динамической системы х = Ах + Dw, х(0) = хо, г = Сх, соответствующим инвариантному эллипсоиду (5). Соответственно если состояние хо принадлежит инвариантному эллипсоиду с матрицей Р, то выход системы г(t) будет находиться в эллипсоиде 8, для всех t > 0.

Теперь можно переформулировать задачу: будем минимизировать ограничивающий эллипсоид, содержащий выход г системы (4).

Теорема 1. Решение I3 задачи trCPCT —> min при ограничениях

АР + РАТ + аР + ^DDт 6 0,   Р > 0, где

А = (А АО) ■    D=(Do) ■ С=<—С1 > ■ а минимизация проводится по матричной переменной Р = РТ Е R(n+m)x(n+m) и скалярному параметру а > 0, определяет матрицу

СРС

Т

ограничивающего эллипсоида для выхода z системы (3).

Доказательство. Введем в рассмотрение квадратичную форму

V(g) = дТQg,    Q> 0, построенную на. решениях системы (4). Вычисляя ее производную в силу системы, имеем

V(g) = (Ад + D w)^T Qg + д^Т Q(Ag + Dw) = д^Т (А^т Q + QA)g + 2g^T QDw.

Для того чтобы траектории системы не вышли за границу эллипсоида £д = {д: gTQg 6 1}, потребуем, чтобы при V(д) > 1 и wTw 6 1 выполнялось условие V(д) 6 0. Иными словами, дТ(АТQ + QA)g + 2wTDTQg 6 0   V (g,w): дТQg > 1, wTw 6 1.       (6)

Применяя 5-теорему [9] с двумя ограничениями, заключаем, что (6) эквивалентно выполнению следующего матричного неравенства при некоторых значениях а, 3 таких, что а > 3 >  0:

Ат Q + QA + aQ QD

DТ Q     -31

По лемме Шура полученное линейное матричное неравенство эквивалентно

А Q + QA + aQ + 3QDD Q 6 0.

Домножив (7) на матрицу Р = Q ¹ слева и справа, приходим к матричному неравенству

АР + РА^Т + аР + pDD^T

6 0;

при ЭТОМ, согласно [10], МОЖНО ПОЛОЖИТЬ 3 = 3ш_ах = а.

Выбирая среди эллипсоидов полученного семейства.

АР + РА^Т + аР + -DD^T 6 0

эллипсоид Р >  0 такой, что соответствующий ему ограничивающий эллипсоид с матрицей СРС ^Т обладает минимальным следом, приходим к утверждению теоремы. Теорема доказана.                                                                               ■

Заметим, что V(д) является квадратичной функцией Ляпунова для системы (4) вне инвариантного эллипсоида с матрицей Р.

3.    Задача синтеза

Рассмотрим линейную непрерывную систему управления:

X = Ах + Ви + D/(t), х(0) = хд, z = /(t) - Сх, где А Е Rnxn, В Е Rnxp, С Е R/xn, D Е Rnx/, x(t) Е Rn — фазовое состояние системы, u(t) Е Rp — управление, z(t) Е Rz — выход системы. Пусть сигнал /(t) Е Rz удовлетворяет условиям (1), (2).

Задача состоит в построении регулятора К в форме статической линейной обратной связи по состоянию

U = К1Х + ^f,

где К1 G R^pxn, К2 G R^px/, который стабилизирует замкнутую систему и минимизирует (по критерию следа) ограничивающий эллипсоид для выхода z. Будем предполагать, что текущее значение сигнала f (t) известно, и поэтому можно его использовать для построения обратной связи.

Рассмотрим расширенную систему

X = Ах + Ви + Df, f = Аof + Dow, z = f (t — Cx,

или, в виде, замкнутом регулятором (8),

X = (А + ВК1)х + (ВК2 + D)f, f = Аof + Dow, z = f — Cx.

(Ю)

Система (10) представима относительно вектора д в следующем матричном виде:

^д=( ⏟

А + ВК1 D + ВК₂

^А о

) ^{д +} U) "■

~

А

~

D

В следующей теореме устанавливается способ нахождения искомого регулятора рассматриваемой системы, а также соответствующий ограничивающий эллипсоид.

Для

̂︀

̂︀

Теорема 2. Решение Р > 0, Ү задачи минимизации

trCPC T —> min

при ограничении

АР + РА^Т + аР + ВҮ + Ү^TВ^Т + -DD^T 6 0,

(И)

где

а минимизация Ү G Rfa+Oxfa+O по состоянию

■'=g .у-   ■=(o,   -=(a, проводится no матричным переменным Р = РТ G R(n+/)x(n+/); и скалярному параметру a > 0, определяет статический регулятор

К = (К1 К 2) = ҮР ^-1

и матрицу

CPC ^T

соответствуюгцего ограничивающего эллипсоида для выхода системы (9).

Доказательство. Применяя теорему 1 к замкнутой системе, приходим к задаче минимизации

tr CPC^T —> min

при ограничении

(

А + ВК1 D + ВК₂

Ао

)^{Р +Р}(

А + ВК1 D + ВК₂

Ао

) ^T + “Р + ¹ ( D )( D ) ^T 6 0, a \J0oy D^OoJ

которое представимо в виде

(^А X) ^{р + р} (о АО)" ⁺ “^{р +} (о)<^л'1 ^ЛУ ^{р +}

^{+ р К K}2f (о У ⁺ 5 (D)(D )" ⁶ °. ¹¹²¹

В матричное неравенство (12) переменные Р, Кі и К2 входят нелинейно. Введя матричную переменную

Ү = (К1 К2) Р, неравенство (12) примет линейный (по переменным Р и Ү) вид (11). Теорема доказана. ■

4.    Пример: двухмассовая система

Продемонстрируем предложенный подход к решению задачи слежения на примере двухмассовой системы [8] (см. рис. 1).

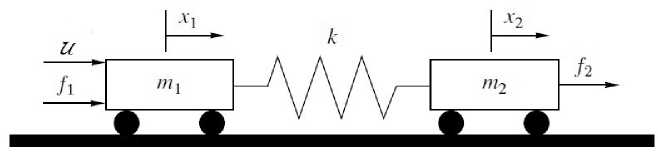
Рис. 1. Двухмассовая система.

Обозначим через хі, «і координату и скорост в левого тела, а через Х2, «2 — координату и скороств правого тела. Тогда.

/хЛ

«1 х = Ж2

«2

еств вектор фазового состояния динамической системы. Пуств к левому телу приложено управляющее воздействие п, а задающий сигнал с компонентами fi и /₂ воздействует на каждое из тел.

Непрерывная модель возмущенных колебаний системы описывается уравнениями х 1 = «1, х 2 = «2,

«1 =

-

к к 1

---Х1 +-- Х2 +-- fi + П,

т1 т2 т1

• ^{к к} . ¹ г

«2 = ---Х1--Х2 +--/2.

т1    т2    т2

Будем считать массы тел и коэффициент упругости пружины единичными. Тогда, в матричной форме имеем х = Ах + Df,

2 = f — Сх, где

/° 1 0 °\ (« °\ м А = —1 0 1 0 ,    D = 0 1 ,    В = 1 о 0 0 1 0 0 о 1 0 —1 0/ 1 0/ \0/ а в качестве матрицы выхода выбрана

1000 ^С 0 10 0 ‘

При

Ло = ( -⁰5   5 ) , Do = (фЭ

- 0 5 - 0 5              - 0 5

с помощвю теоремы 2 найдем ограничивающий эллипс выхода и соответствующий регулятор.

Заметим, что естественно потребоватв ограничения на величину управления вида

||u(t)| 6 ц     V t >  0.                                        (13)

Достаточное условие выполнения ограничения (13) установлено следующей леммой.

Лемма 1 ([11]). Условие

(' Й).....

гарантирует выполнение условия (13) внутри инвариантного эллипсоида с матрицей Р.

Это условие добавляется в качестве дополнительного ограничения в формулировку теоремы 2.

Итак, полагая

Ц = 5, находим регулятор к = (-31,3569 ⏟

- 17 , 3058 9 , 4955    - 17 , 2320

26 , 2767 9 , 5308

⏟⏞ К

К и матрицу ограничивающего эллипса:

СРС

т

0 , 3044

- 0 , 1383

- 0 , 1383 0 , 6609

,

при этом tr CpC ^t = 0 , 9653.

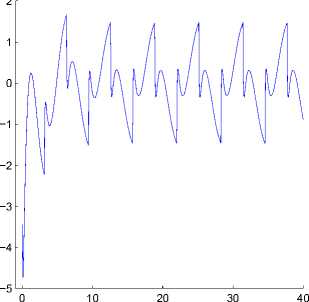
На рис. 2 слева показан найденный ограничивающий эллипс выхода, а также траектория выхода системы при некотором начальном состоянии системы вне инвариантного эллипсоида и возмущении w(t) = sign sin t; справа показан соответствующий график управляющего воздействия.

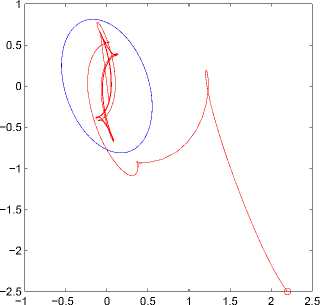
Рис. 2. Ограничивающий эллипс выхода, траектория выхода, системы и управление

Заметим, что, не используя информацию о текущем значении сигнала /(t) (то есть при К = 0), получим регулятор, который также стабилизирует систему (9); однако при этом ограничивающий эллипсоид окажется примерно в 6 раз больше по критерию следа.

5.    Заключение

В статье предложен подход к построению обратной связи в одной из постановок линейной задачи слежения. Подход основан на. методе инвариантных эллипсоидов, применение которого позволило переформулировать исходную проблему в терминах линейных матричных неравенств и свести поиск ограничивающего эллипсоида, для выхода, системы к задаче полуопределенного программирования, легко решающейся численно. Эффективность метода. продемонстрирована, на. примере двухмассовой системы.