Применение метода изменяющихся вероятностей для задач оптимального размещения на сети
Автор: Антамошкин Александр Николаевич, Казаковцев Лев Александрович
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 5 (57), 2014 года.
Бесплатный доступ
Рассматривается p-медианная задача оптимального размещения на графе (сети), являющаяся популярной моделью как в логистических задачах (оптимальное размещение транспортной, телекоммуникационной и иной инфраструктуры), так и опосредованно в задачах кластерного анализа, распознавания образов, в теории оценивания. Цель p-медианной задачи на графе (сети) заключается в нахождении определенного числа вершин (узлов) таких, чтобы суммарное расстояние от всех узлов сети до ближайшей из выбранных вершин (узлов) было минимальным. Для приближенного решения рассматриваемой неразрешимой (в общем случае) за полиномиальное время задачи предложен эвристический алгоритм, основанный на идеях метода изменяющихся вероятностей, являющегося методом случайного поиска с адаптацией. Идея алгоритма заключается в случайном выборе вершин в соответствии с заданными вероятностями выбора каждой из вершин и изменении этих вероятностей для каждой из выбранных вершин и вершин в некоторой ее окрестности в зависимости от достигнутого значения целевой функции (т. е. в зависимости от суммарного расстояния от каждой из вершин графа до ближайшей из выбранных вершин). При создании алгоритма для p-медианных задач с большой размерностью и вычислительной сложностью ставится задача оптимального использования вычислительных мощностей. Эффективность алгоритма подтверждена экспериментальной проверкой на тестовых примерах из библиотеки ORLIB. Также приведены результаты работы комбинированного алгоритма - комбинации предложенного алгоритма с процедурой локального поиска для решения данной задачи. Экспериментально показано, что результаты такой комбинации превосходят результаты оригинального многократных запусков алгоритма, реализующего локальный поиск из случайным образом выбранных вершин. Кроме того, в работе экспериментально показано, что для небольших задач алгоритм способен получить точное решение задачи.
Дискретная оптимизация, p-медианная задача, методы случайного поиска, задачи размещения
Короткий адрес: https://sciup.org/148177339
IDR: 148177339 | УДК: 519.6
Application of the probability changing method for optimal location problems on a network
In this paper, the authors consider the p-median optimal location problem on a graph (network) which is a popular model for both logistic problems (optimal transportation, telecommunication and other infrastructure elements placement) and problems of cluster analysis, pattern recognition and estimation theory. The aim of the p-median problem on a graph (network) is to find the given number p of vertices of a graph such that the total distance from each vertex to the nearest chosen vertex reaches its minimum. To solve this NP-hard (in general) problem approximately, the authors propose a heuristic algorithm based on ideas of the probability changing method which is a random search method with adaptation. The idea of the proposed algorithm is based on random choosing of vertices in accordance with the given probabilities of choosing each of them. The probabilities for every chosen vertex and its neighborhood alter depending on the value of the objective function (i.e. in accordance with the total distance from each of the vertices to the nearest chosen vertex). For the algorithm for the large-scale p-median problems, a problem of optimal use of computational capacity is important. The effectiveness of the proposed algorithm was proved experimentally on test datasets from the ORLIB (special dataset library for operations research). In addition, the authors illustrate the results for the proposed algorithm combined with a local search procedure for the considered problem. The experiments show that the results of such combination exceed the results of the multiple start of the local search procedure from randomly chosen vertices. In addition, the experiments demonstrate the ability of the proposed algorithm to reach an exact solution for small problems.
Текст научной статьи Применение метода изменяющихся вероятностей для задач оптимального размещения на сети
Введение. Задачи размещения – класс задач оптимизации, в которых основными параметрами выступают координаты (местоположения) точек в некотором пространстве (непрерывном либо дискретном) и расстояния между ними [1; 2]. Задачи находят непосредственное практическое применение как при размещении производств, сетей, объектов инфраструктуры, датчиков и т. п., так и при решении задач кластерного анализа, распознавания образов, теории оценивания [3].
Задача Вебера (Ферма–Вебера) [1] – задача о поиске точки, сумма взвешенных расстояний от которой до известных точек (точек требования) минимальна, является обобщением простейшей задачи Ферма о нахождении точки, сумма расстояний от которой до трех известных точек минимальна, и имеет, в свою очередь, множество обобщений, главные из которых – множественная задача Вебера [4] и p -медианная задача [5] на плоскости или на сети:
N
F (X1, X2,..., XM ) = ^, w, min L (Xj, Ai) ^ min, (1) i=1 j e{1, m } где {Ai| i = 1,N} – множество точек требования; {Xj | j = 1,p} – множество размещаемых точек; wi – весовой коэффициент i-й точки требования; L(.) – функция расстояния.
В общем случае задача не может быть решена за полиномиальное время, алгоритм с полиномиальным временем известен только для деревьев [6]. Использование релаксации Лагранжа [7] позволяет получать приближенные решения задач размерности до n = = 3 795. Под размерностью задачи будем понимать число вершин графа.
Непрерывные задачи размещения в евклидовой метрике (l2), а также в метриках l1 (прямоугольной или манхэттенской) и l∞ (чебышевской) изучены и созданы универсальные алгоритмы на основе процедуры Вайсфельда, исследована их вычислительная сложность [8; 9]. Решение тех же задач, например с запретными зонами [10], уже не является тривиальным. В практических задачах при использовании евклидовой или прямоугольной метрики такие модели являются достаточно грубым приближением [11; 12], поскольку не учитывают свойства пространства и средств транспортировки, в частности, наличие и качество дорог, барьеры, рельеф и т. п. Нередко функция расстояния является решением другой (вложенной) оптимизационной задачи и задается в этом случае алгоритмически [12]. Таким образом, и в случае задачи, изначально сформулированной в виде задачи Вебера, зачастую целесообразной является ее дискретизация [13; 14]. Такие задачи можно рассматривать как p-медианные задачи на полном графе. Компромиссные подходы, сочетающие в формулировке задачи элементы дискретного и непрерывного подходов, рассмотрены в [15–17].
В p -медианной задаче на сети [5], которая рассматривается в настоящей работе, поиск решений (медиан) осуществляется в известном конечном множестве узлов графа (сети). В данной задаче требуется выбрать p вершин таким образом, чтобы сумма взвешенных расстояний от каждой из вершин графа до ближайшей из выбранных вершин была минимальной. Такое множество будем называть p -медианой, а элементы этого множества – медианами.
Эвристические методы случайного поиска не гарантируют нахождение точного решения, но они статистически оптимальны: процент задач, решенных «почти оптимально», растет с ростом размерности задачи [18] (т. е. с ростом числа булевых переменных). При решении дискретных задач размещения применяется генетический алгоритм и другие методы [19; 20].
Изначально разработанный для решения безусловных задач псевдобулевой оптимизации, метод изменяющихся вероятностей (МИВЕР) [18; 21; 22] – это метод случайного поиска, который некоторыми авторами рассматривается как специфический вариант генетического алгоритма [23], в котором происходит полная смена поколения особей от итерации к итерации, а процедуре скрещивания соответствует процедура адаптации вероятностей и генерация нового поколения в соответствии с новыми вероятностями.
Алгоритм 1. Метод изменяющихся вероятностей.
Дано: f b ( X ) – псевдобулева целевая функция – вещественная функция N булевых переменных, R – предельное число итераций. Здесь X = ( x 1 , ..., x N ) – вектор булевых переменных.
-
1. Присвоить k = 0. Установить начальные значения вероятностей P k = { p k 1 , p k 2 , ..., p kN }, где p kj = = P { x j = 1}. Здесь и далее индекс k – номер итерации. Корректный выбор начальных значений P 0 – важная проблема, особенно при переходе к условной оптимизации.
-
2. В соответствии с вектором распределений P k генерируется набор N v векторов Xki, i e {1,..., N v }, каждый элемент p kj вектора P k задает математическое ожидание генерации единицы в j -й компоненте векторов X ki . Число генерируемых на каждом шаге векторов N v называется размерностью популяции по аналогии с генетическим алгоритмом.
-
3. Вычисляется значение fb ( Xki ) для каждого из сгенерированных векторов.
-
4. Выбираются некоторые значения целевой функции f b ( X ki ) и соответствующие векторы X ki , например, экземпляры сгенерированных векторов с максимальным и минимальным значением f b ( X ki ).
-
5. На основе результатов шага 4 модифицируется вектор P k .
-
6. k = k +1, если k < R , то переход к шагу 2. Возможны другие условия останова.
-
7. Иначе останов.
В задачах условной оптимизации применяются специальные модификации метода. Например, параллельные модификации алгоритма, предложенные в [24], позволяют решать задачи «рюкзачного» типа большой размерности (десятки тысяч переменных), а для задачи о коммивояжере, сформулированной в булевых переменных, число переменных может достигать 106.
При создании алгоритма для p -медианных задач с большой размерностью и, соответственно, вычислительной сложностью, попутно должны быть решены задачи оптимального использования вычислительных мощностей. Прогнозируемое появление и распространение в ближайшем будущем персональных кластеров делают оправданной разработку параллельных алгоритмов размещения для систем с распределенной памятью. Эффективность параллельных алгоритмов на базе метода изменяющихся вероятностей, описанных в [13; 25; 26], для задач большой размерности доказана экспериментально.
Целью данной работы является адаптация метода изменяющихся вероятностей для решения p -медианной задачи и исследование применимости полученного алгоритма для решения задач большой размерности ( n > 500).
Постановка задачи, алгоритм расчета значения целевой функции. Пусть G = ( V , E) - ненаправленный связный граф (сеть), V = { v ь ..., vn } - множество вершин, E = { e i | i = 1, m} - множество ребер, e i = ( V j ,vk ) , J e {1,..., n }, k e {1,..., n } V i = 1, m без петель, т. е. e i * ( V j ,V j ) , V i = 1, m , j = 1, n - Каждому ребру e i поставлена в соответствие его длина l i > 0 (для e i = ( v j ,vk ) введем обозначение l j, k = l i ), каждой j -й вершине поставлен в соответствие вес W j > 0 . Для любой пары вершин ( iJ ) определена функция расстояния L ( iJ ) -длина кратчайшего пути между данными вершинами:
L ( i , j ) = Е l k = pmin V l k ,
-
* P path e Pi.J .p
k e Pi j k e Ppath где P* - множество ребер, составляющих кратчайший путь между i-й и j-й вершинами; Pij - множество всех возможных путей между данными вершинами; Ppath - любой путь из множества возможных путей Pij.
Тогда p-медианную задачу можно сформулировать как min _ f (m1,..., mp) =
^ 1,..., m p e{1, n } 4
n (2)
= min _ V w, min L ( m, , i ) , p < n.
m1, ..., m p ={1, n } = j e{1, p } V J /
Введем дополнительные обозначения.
C i = { k e {1, n } | 3 e j = ( v,,vk ) , j e {1, m }} - множество индексов окружения г -й вершины (ее окрестности первого порядка);
l * = min L ( m . ,i ) - длина кратчайшего пути из i -й
J=1,p v J ’ вершины до ближайшей из p вершин m 1,..., mp.
Значения функции f ( m 1,..., mp ) вычислим с помощью модификации алгоритма Дейкстры [27]:
Алгоритм 2 . Расчет значения целевой функции.
Дано: индексы p выбранных вершин m 1 ,..., m p .
-
1. Присвоить l * = + mV i = 1, n .
-
2. Присвоить lm i = 0 V i = 1, p .
-
3. Присвоить V = { m 1,..., mp } ; V = V .
-
4. Пока V ** * 0 , цикл:
-
4.1. Пока V'= 0 .
-
4.2. Для i e V** цикл:
-
4.2.1. Для j e C i цикл:
-
4.2.1.1. Если j t V *, тогда V = V и { j }; l * =l * +l , j .
-
4.2.1.2. Иначе, если l * > l * + l i,j , тогда l * = l * +li ,j .
-
4.2.1.З. Конец цикла 4.2.1.
-
-
4.2.2. Конец цикла 4.2.
-
-
4.3. Присвоить V** = V ; V* = V * и V .
-
4.4. Конец цикла 4.
-
-
5. Возврат f ( m 1 ,..., m p ) = V^ wl i * .
*
* T7** ТЛ*
i =1
Метод изменяющихся вероятностей является методом псевдобулевой оптимизации, для его применения целевая функция должна быть выражена как функция булевых переменных.
Введем новые переменные x 1 ,..., xn :
-
[ 1, i e { m 1 ,..., m p };
x i = i (3)
-
[ 0, i t { m 1 ,..., m p }.
В случае булевых переменных задача имеет ограничение
n
-
V x i = p . (4)
i =1
Обратный переход к исходным целочисленным переменным осуществляется следующим образом:
{ m 1 ,..., m p } = { i | x = 1, i = 1, n }.
Задачу с псевдобулевой целевой функцией можно сформулировать следующим образом:
-
f , ( x 1 , ..., X n ) = f ( { j | X j = 1, j= 1, n } ) =
n
= S w min L ( j,i )
i=1 {j\Xj =1, J =1, n } с ограничением (4).
В данном виде задача может быть решена различными методами псевдобулевой оптимизации, в том числе и методом изменяющихся вероятностей. Предлагаемый нами алгоритм на базе метода изменяющихся вероятностей учитывает условие (4) на этапе генерации очередной популяции векторов (шаг 2 алгоритма 1).
Алгоритм на базе метода изменяющихся вероятностей. Пусть L max - диаметр графа (максимальное из расстояний между парами вершин):
Lmax = max L ( i, j ), i, jе{1, ..., n} lavg — средняя длина ребра:
m lavg = E j m .
j=1
Наш алгоритм основан на следующих предположениях:
-
1. При
-
2. Если в решении { m 1,..., m p } для любых двух вершин v m и v mj расстояние L ( m i , m j ) мало, велика вероятность того, что при замене одной из компонент решения m j - на к -ю точку такую, что при L ( m i , к ) >> >> L ( m i , m j ), значение целевой функции для нового решения будет ближе к оптимальному:
l avg / L max ^ 0 (5)
свойства задачи размещения на сети приближаются к свойствам непрерывной задачи, а именно: при замене в решении { m 1,..., mp } любой m i -й вершины на другую j -ю вершину такую, что L ( j' , m i ) мало, изменение значения целевой функции будет малым.
fm 1 , ..., m i , ..., m j , ..., m p ) > f ( m 1 , .., m i , ..., к , ..., m p ).
Под «малым» расстоянием будем подразумевать L ( m i , m j ) < L 0, L 0 = const.
Эксперимент для доказательства данного утверждения приведен ниже.
Наша модификация алгоритма 1 сводится к изменению на шагах 2 и 5.
На шаге генерации экземпляров вектора X должно быть учтено ограничение (4). Это достигается следующим алгоритмом.
Алгоритм 3 . Генерация одного члена популяции на шаге 2 алгоритма 1.
Дано: вектор вероятностей P = ( p i , ..., p n ), число вершин в решении p .
-
1. Присвоить х = 0 .
-
2. Пока | х | < p , цикл:
-
2.1. r = Random ( ) • £>_ / ; 5 = 0.
-
-
2.2. Для каждого j е {1, n } цикл:
-
2.2.1. Присвоить 5 = 5 + p j .
-
2.2.2. Если 5 > r , тогда х = X ° { j }; прервать цикл 2.2.
-
2.2.3. Конец цикла 2.2.
-
-
2.3. Конец цикла 2.
-
3. Возврат х.
j =1
Результатом алгоритма является множество х• Соответствующий вектор Xki , i е {1, ..., Nv } (см. шаг 2 алгоритма 1), может быть получен согласно формуле (3).
Здесь Random () - функция, генерирующая случайные значения в интервале [0,1) с равномерным распределением.
Данный алгоритм имеет следующую геометрическую интерпретацию. Расположим на числовой прямой, начиная от точки 0, смежные отрезки 5 1, ..., 5n , причем длина i -го отрезка равна p i , i = 1, n . Длина
n суммарного отрезка равна E Fj• Выберем случайную j=1
точку r на суммарном отрезке. Определим, какому из отрезков 5 1, ..., 5n она принадлежит. Вероятность попадания r в отрезок 5 i пропорциональна p i . Дополним множество х соответствующим индексом. Повторяем, пока в х не наберется p индексов.
В следующей версии алгоритма снижается вероятность генерации решений с близкими друг к другу вершинами:
Алгоритм 4 . Модифицированная процедура генерации члена популяции.
Дано: вектор вероятностей P = ( p 1, ..., p n ), число вершин в решении p .
-
1. Присвоить х = 0 .
-
2. Пока | х | < p , цикл:
-
2.1. P* = P .
-
2.2. r = Random ( ) -]^ p * ; 5 = 0.
-
-
2.3. Для каждого j е {1, n } цикл:
-
2.3.1. Присвоить 5 = 5 + p * .
-
2.3.2. Если 5 > r , тогда х = х ° { j }; j' = j ; прервать цикл 2.3.
-
2.3.3. Конец цикла 2.3.
-
-
2.4. Для каждого j е { к е {1, n }| L ( j'/ )
0} присвоить p * = p * ■ L ( j, j' ) / L 0 ; конец цикла 2.4. -
2.5. Конец цикла 2.
-
3. Возврат х.
j =1
Алгоритм 4 дополнительно оперирует вторым временным вектором вероятностей P *, компоненты которого меняются по ходу генерации элементов множества х. Если на очередной итерации множество дополнено индексом j' , то вероятности p j , соответствующие вершинам, лежащим от вершины v j на расстоянии, не превышающем L 0, уменьшаются, дабы избежать генерации близких друг к другу вершин врешении.
Шаг 5 алгоритма 1 (адаптация вектора вероятностей) на к -й итерации выполняется по формулам
Р к,Д p ( к -1 ) , i d k , i ;
d kb,i
w d k,i
d k,i =dL; dk/;
1
+ L
0
/(1
+ L
(
i
b
,
i
)),
L
(
i
,
i
b
)
1,
L ( i , i b ) > L 0 ;
1
+ L
0
/(1
+ L
(
i
w
,
i
)),
L
(
i
,
i
w
)
1,
L ( i , i w ) > L 0 .
Здесь ib и iw – ближайшие к i-й вершине такие, что bbww b w i g x , i g X , где X и X — те экземпляры сгенерированных алгоритмом 2 или алгоритмом 3 множеств индексов, входящих в решение вершин χ , в которых целевая функция принимает лучшее (минимальное) и худшее (максимальное) значения.
Следует отметить, что дискретизированную задачу Вебера, описанную в [13], можно считать частным случаем рассматриваемой в настоящей работе задачи на сети, вследствие чего предлагаемые алгоритмы имеют некоторое сходство.
Результаты экспериментов. Сначала докажем экспериментом состоятельность предположения 2.
Алгоритм 5 . Дано: граф G c n вершинами, количество вершин в решении р , предельное расстояние L 0 .
-
1. Присвоить N = 0, N > = 0.
-
2. Выбрать случайным образом p индексов вершин из n : m 1 , ..., m p g {1, n} .
-
3. Если не существуют i, j g {1, p }: L ( m i , m j )
0 , то перейти к шагу 2. -
4. Выбрать случайным образом k g {1, n} . Если L ( k , m j ) < L 0 , то повторить шаг 4.
-
5. Если f ( m i ,..., m i ,..., m j ,..., m p ) > f ( m i ,..., m i ,
-
6. Присвоить N = N + 1; если N < 1 000, то перейти к шагу 2.
-
7. Останов, возврат p > = n > / 1000 .
..., k , ..., mp ), то N > = N > + 1.
Результаты работы алгоритма 5 для автоматически сгенерированных задач (см. алгоритм 6) и для задач pmed22 и pmed39 из набора тестовых задач ORLIB [28] представлены на рис. 1. Оценка вероятности дана в процентах. Для задач pmed22 и pmed39, благодаря специфике их генерации [28], соотношение lavg / L max велико, и условие предположения 2 выполняется лишь при очень малых значениях L 0 (много меньших, чем l avg ).
Для целей тестирования по основной теме статьи мы использовали автоматически сгенерированные тестовые задачи (см. алгоритм 6), схема одной из которых показана на рис. 2, а . Здесь длины ребер изображены в масштабе, диаметр вершин на изображении соответствует их весовому коэффициенту. На рис. 2 также изображено полученное нашим алгоритмом решение для p = 32. Здесь вершины, входящие в решение, обведены. Расстояние от каждой вершины до ближайшей вершины, входящей в решение, отмечено соответствующим цветом: вершины с меньшим расстоянием изображены темным цветом, с большим – светлым.
Алгоритм 6. Генератор тестовых задач.
Дано: n – число вершин.
-
1. Для каждого i g { 1, n } цикл: a i = Random () • 500; bi = Random () ∙ 500, wi = 0,5 + Random () ∙ 10; конец цикла.
-
2. Заполнить матрицу смежности A нулевыми значениями; множество ребер E = 0 .
-
3. Для i g { 1, n } цикл:
-
3.1. Если i > 0,7 n , тогда D i = 1.
-
3.2. Иначе, если i > 0,3 n , тогда Di = 2.
-
3.3. Иначе D i = 3 + [ Random () ∙ 4].
3.4. Для d g { 1,£ A J
j =1
цикл:
-
-
4. Останов, возврат результатов: матрица смежности A , множество ребер E , длины ребер l i,j , где ( i , j ) g E , весовые коэффициенты w, , где i g { 1, n } .
j = argmin j ^} , ■. (I a - a j I+ b i - b I); Au = 1; A , =1; добавить к множеству E ребро ( i,j ); l i j = | a i- - a j | + | b i- - b j |; конец цикла.
В алгоритме 6 Random () – функция, генерирующая случайные значения в интервале [0,1) с равномерным распределением. На шаге 3.4 ведется поиск вершин, близких к i -й, которые соединяются с ней ребрами, вследствие чего lavg / L max мало (см. условие (5)).
Ход решения (изменение значений вероятностей) проиллюстрирован на рис. 3, где вершины, для которых вероятность попадания в экземпляр решения максимальна, изображены светлым цветом, вершины с минимальной вероятностью – темным.
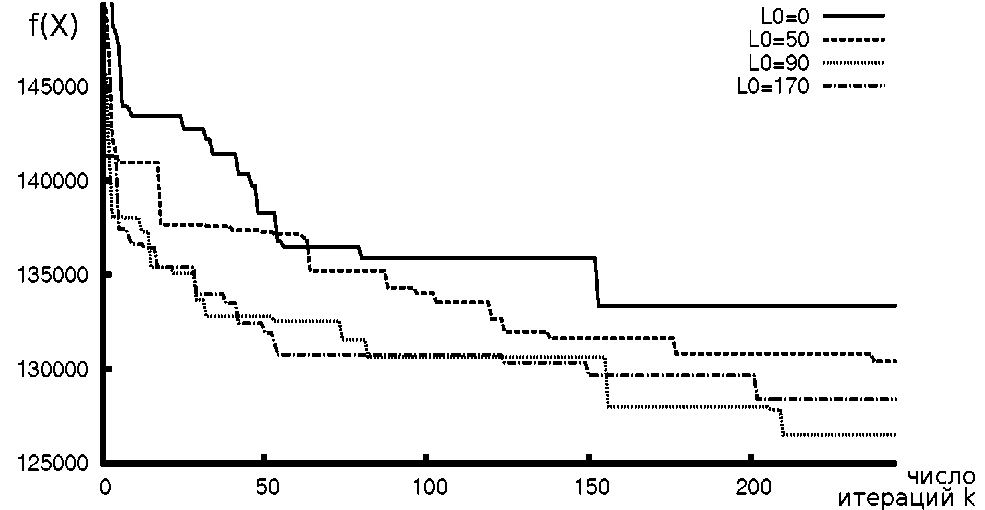
Диаметр окрестности L 0 – важный параметр, во многом определяющий эффективность работы алгоритма. При p = 12 сравнение результатов при различных значениях этого параметра показано на рис. 4.
Для построения графика зависимости достигнутого значения целевой функции от количества выполненных итераций k (см. шаг 6 алгоритма 1) в алгоритм добавлены специальные команды, записывающие значение целевой функции в массив. Для задачи, схема которой дана на рис. 2 ( n = 500, p = 12), выполнялось по 10 запусков алгоритма с каждым из значений L o g {1, 3, 10, 25, 50, 90, 120, 170, 250, 350, 500, 750}. На графике показаны усредненные значения для 10 запусков, достигнутые после каждой итерации. Линии L 0 = 0 соответствует алгоритм, не учитывающий соседство вершин, в котором генерация поколений экземпляров векторов X осуществляется согласно алгоритму 3. Наилучшие результаты достигаются при L 0 = 90. Оптимальное значение параметра L 0 зависит от параметра p . Тем не менее при изменении параметра L 0 в широком диапазоне ( L 0 = 10...350) для данной задачи алгоритм стабильно показывает лучшие результаты, чем «классический» алгоритм схемы МИВЕР с генерацией экземпляров вектора X согласно алгоритму 3.
Применимость алгоритма для задач большой размерности проверена на тестовом примере с n = 5 000 (рис. 5). Использовалась вычислительная система DEPO X8Sti (6-core CPU Xeon X5650 2.67 GHz, 12Gb RAM), HyperThreading отключен, компилятор ifort с опцией полной оптимизации (-О3).
Сравнение с алгоритмами, дающими точное решение, затруднено вследствие высокой вычислительной сложности задач. Так, например, метод ветвей и границ при соответствии задачи условию (5) практически вырождается в процедуру полного перебора. Методы, предложенные Хакими [5], также имеют экспоненциальную асимптотическую сложность. Для p = 3 сравнение результата на сети с 170 вершинами, полученного нашим алгоритмом и алгоритмом случайного поиска без адаптации (хаотический поиск, при котором на каждой итерации случайным образом выбираются p вершин), с точным результатом, полученным полным перебором (горизонтальная асимптота), показано на рис. 6. Для построения графика к шагу 6 алгоритма 1 добавлены команды, которые через каждые 10 итераций фиксируют в специальном массиве достигнутое значение целевой функции и время с момента запуска алгоритма. Запуск алгоритма 1 и алгоритма хаотического поиска осуществлен по 10 раз, на рис. 6 показан усредненный (для 10 запусков) результат хаотического поиска и худший (из 10 запусков) результат нашего алгоритма на базе метода изменяющихся вероятностей. Следует отметить, что модифицированный алгоритм как улучшает усредненные результаты 10 запусков, так и несколько сужает разброс результатов. Так, анализ наихудших значений, полу- ченных алгоритмами после 10 запусков, дает картину, аналогичную на рис. 6. Вычислительная сложность полного перебора эквивалентна 402 220 итерациям алгоритма 1 (требуется 4 826 640 вычислений целевой функции, алгоритм генерирует на каждом шаге 12 экземпляров вектора X).
Скомбинируем предложенный алгоритм с процедурой локального поиска. Дополним алгоритм 2 шагом 0:
Шаг 0 алгоритма 2: запустить процедуру локального поиска из начального множества вершин с индексами m 1, ..., mp .
Мы будем использовать простейший [29] из множества методов локального поиска для данной задачи [30] – поиск в окрестности, состоящей из вершин, смежных с выбранными вершинами m 1, ..., mp . Сравнение результатов полученного алгоритма с результатами многократного запуска процедуры локального поиска из случайно (хаотически) выбранных вершин для сгенерированной задачи большой размерности показано на рис. 7.
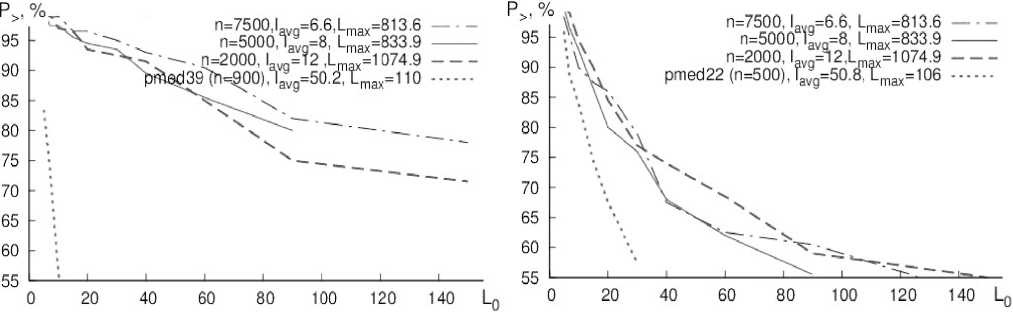
Рис. 1 . Соотношение оценки вероятности выполнения условия предположения 2 и предельного расстояния L 0 для сгенерированных задач и задач из библиотеки ORLIB (pmed39 и pmed22). Указаны параметры задачи: n – число вершин сети, l avg – среднее, L max – максимальное расстояние между вершинами в сети
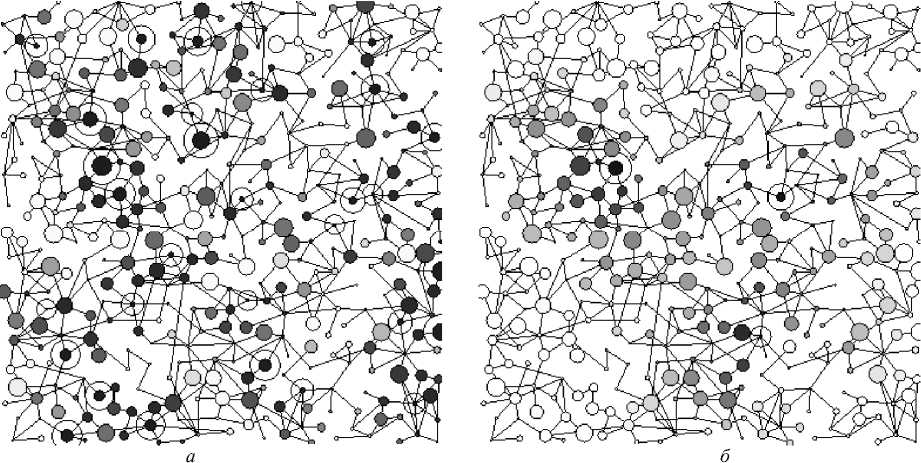
Рис. 2. Схема сгенерированной задачи ( n = 500) и ее решения (обведены окружностями): а – решение для р = 32; б – решение для р = 3

3-й шаг б-й шаг 10-й шаг
Рис. 3. Ход решения (изменение значений вероятностей) для p = 3, L 0 = 100
F(X)
Рис. 4. Сравнение результатов с различными значениями параметра L 0, p = 12
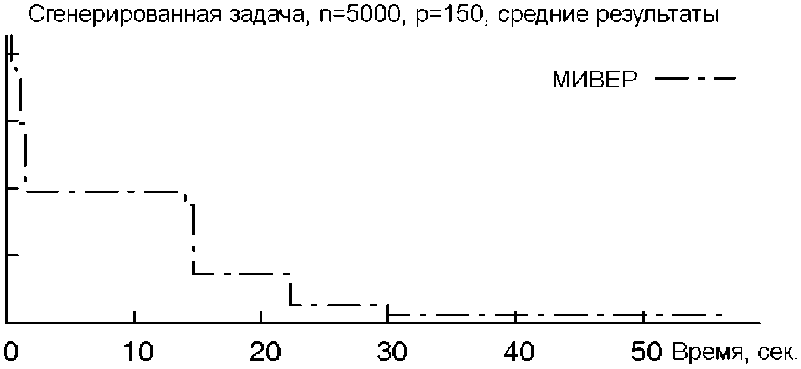
Рис. 5. Усредненные результаты для 10 попыток запуска тестового примера с n = 5 000
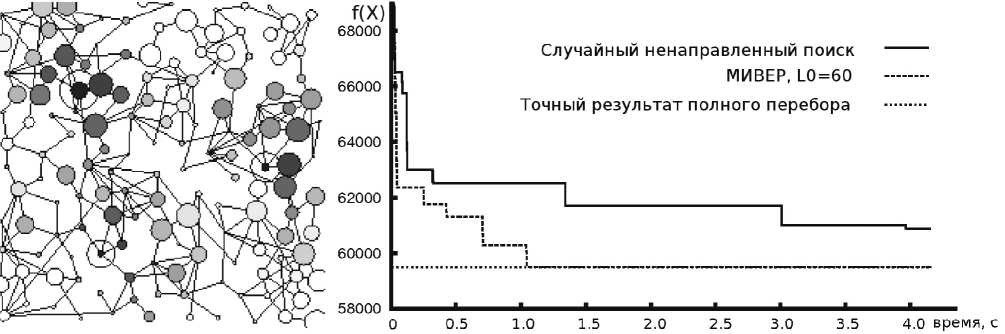
Рис. 6. Схема задачи с оптимальным решением и сравнение результата алгоритма для p = 3 с результатом хаотического поиска и полного перебора
F(X)
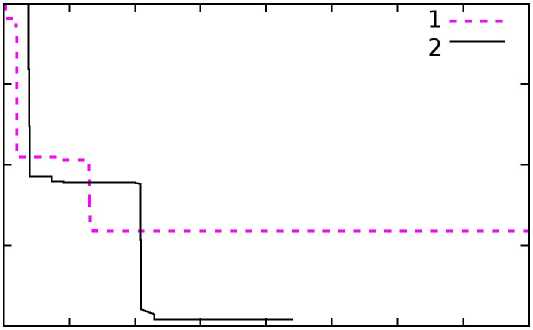
100 150 200 250 300 ВрвМЯ,С
Рис. 7. Сравнение результатов комбинированного с локальным поиском алгоритма с результатами локального поиска из хаотически выбранных вершин. Cгенерированная задача, n = 7500, p = 10: 1 – комбинированный алгоритм, 2 – локальный поиск
Заключение. Предложенный эвристический алгоритм на базе метода изменяющихся вероятностей может быть использован для решения p -медианной задачи на сети при условии, что длины ребер сети много меньше, чем ожидаемая длина пути между произвольно выбранными вершинами. Поиск оптимальных параметров алгоритма остается темой дальнейших исследований.
Список литературы Применение метода изменяющихся вероятностей для задач оптимального размещения на сети
- Wesolowsky G. The Weber problem: History and perspectives//Location Science. 1993. Vol. 1. P. 53.
- Drezner Z., Wesolowsky G. O. A Trajectory Method for the Optimization of the Multifacility Location Problem with lp Distances//Management Science. 1978. Vol. 24. P. 1507-1514.
- Osinuga I. A., Bamigbola O. N. On the Minimum Norm Solution to Weber problem//SAMSA Conference Proceedings. Windhoek, 2007. P. 27-30.
- Cooper L. An extension of the generalized Weber problem//Journal of Regional Science. 1968. Vol. 8, Iss. 2. P. 181-197.
- Hakimi S. L. Optimum locations of switching centers and the absolute centers and medians of a graph//Operations Research. 1964. Iss. 12(3). P. 450-459.
- Kariv O., Hakimi S. L. An algorithmic approach to network location problems. II. The p-medians//SIAM Journal on Applied Mathematics. 1979. Vol. 37(3). P. 539-560.
- Avella P., Sassano A., Vasil’ev I. Computational Study of Large-Scale p-Median Problems//Mathematical Programming. 2007. Vol. 109(1). P. 89-114.
- Masuyama, S., Ibaraki T., Hasegawa T. The Computational Complexity of the m-Center Problems on the Plane//The Transactions of the Institute of Electronics and Communication Engineers of Japan. 1981. Vol. 64E. P. 57-64.
- Megiddo N., Supowit K. On the Complexity of Some Common Geometric Location Problems//SIAM Journal on Computing. 1984. No. 13. P. 182-196.
- Забудский Г. Г., Нежинский И. В. Решение задачи размещения в евклидовом пространстве с запрещенной областью//Вестник Омского университета. 1999. № 2. С. 17-19.
- Morris J. G. Convergence of the Weiszfeld Algorithm for Weber Problems Using a Generalized “Distance” Function//Operations Research. 1981. Vol. 29, No. 1. P. 37-48.
- Wesolowsky G. O, Love R. F. A Nonlinear Approximation Method for Solving a Generalized Rectangular Distance Weber Problem//Management Science. 1972. Vol. 18, No. 11. P. 656-663.
- Kazakovtsev L. A. Adaptation of the Probability Changing Method for Weber Problem with an Arbitrary Metric//Facta Universitatis series Mathematics and Informatics, University of Nis. 2012. Vol. 27, No. 2. P. 239-254.
- Антамошкин А. Н., Казаковцев Л. А. Алгоритм случайного поиска для обобщенной задачи Вебера в дискретных координатах//Информатика и системы управления. 2013. Вып. 1. C. 87-98.
- Single-facility Weber Location Problem Based on the Lift Metric/P. S. Stanimirovic //Facta Universitatis series Mathematics and Informatics. 2012. Vol. 27, No. 2. P. 175-190.
- Gugat M., Pfeiffer B. Weber problems with mixed distances and regional demand//Math. Meth. Oper. Res. 2007. Iss. 66. P. 419-449.
- Bischoff M., Fleischmann T., Klamroth K. The Multi-Facility Location-Allocation Problem with Polyhedral Barriers//Computers and Operations Research. 2009. No. 36. P. 1376-1392.
- Антамошкин А. Н., Сараев В. Н. Метод изменяющихся вероятностей//Проблемы случайного поиска. Рига: Зинатне. 1988. Вып. 11. С. 26-34.
- A Comprehensive Study of Optimization Algorithm for Wireless Coverage in Indoor Area/A. W. Reza //Optimization Letters. 2012. Doi 10.1007/s11590-012-0543-z. URL: http://link.springer.com/article/10.1007 %2Fs11590-012-0543-z?LI=true (дата обращения: 10.05.2013).
- Alp O., Erkut E., Drezner Z. An Efficient Genetic Algorithm for the p-Median Problem//Annals of Operations Research. 2003. Vol. 122, Iss. 1-4. P. 21-42.
- Antamoshkin A., Saraev V On Definition of Informative Subsystem of Signs in the Pattern Recognition Problem//Computers and Artificial Intelligence. 1985. Vol. 4, Iss. 3. P. 245-252.
- Antamoshkin A. Brainware for Searchal Pseudoboolean Optimization//Tr. оf Tenth Prague Conf. on Inf. Theory, Stat.Dec. Functions, Random Processes. Prague: Academia. 1987. Vol. 10A-B. P. 203-206.
- Дегтерев А. С., Канашкин Ф. В., Сумароков А. Д Обобщение генетических алгоритмов и алгоритмов схемы МИВЕР //Электронный журнал «Исследовано в России». 2004. Т 7. С. 16581665. URL: http://zhurnal.ape.relarn.ru/articles/2004/153.pdf (дата обращения: 13.05.2013).
- Казаковцев Л. А., Ступина А. А. Параллельная реализация метода изменяющихся вероятностей//Современные проблемы науки и образования. 2012. № 4. URL: www.science-education.ru/104-6810 (дата обращения: 31.10.2012).
- Kazakovtsev L. A. Random Constrained PseudoBoolean Optimization Algorithm for Multiprocessor Systems and Clusters//ICUMT 2012, International Congress on Ultra-Modern Telecommunications. IEEE Press. S-Petersburg, 2012. P. 650-656.
- Казаковцев Л. А. Параллельный алгоритм случайного поиска с адаптацией для систем с распределенной памятью//Системы управления и информационные технологии. 2012. № 3 (49). С. 11-15.
- Dijkstra E. W. A note on two problems in connexion with graphs//Numerische Mathematik. 1959. Vol. 1. P. 269-271.
- Beasley J. E. OR-Library: distributing test problems by electronic mail//Journal of the Operational Research Society. 1990. Vol. 41, No. 11. P. 1069-1072.
- Antamoshkin A. N., Kazakovtsev L. A. Random Search Algorithm for the p-Median Problem//Informatica (Ljubljana). 2013. Vol. 37(1). Рp. 267-278.
- Scatter Search and Path Relinking: Fundamentals, Advances and Applications/M. G. C. Resende //Handbook of Metaheuristics. 2nd ed./M. Gendreau and Y. Potvin (editors). Springer, 2010. Pp. 87-107.


