Применение метода эластичной ленты для поиска пути с минимальным перепадом энергии

Полуян С. В., Елизаров А. А., Ершов Н. М. Применение метода эластичной ленты для поиска пути с минимальным перепадом энергии // Системный анализ в науке и образовании: сетевое научное издание. 2023. № 3. С. 60-65. EDN: THTUFZ. URL :

Статья находится в открытом доступе и распространяется в соответствии с лицензией Creative Commons «Attribution» («Атрибуция») 4.0 Всемирная (CC BY 4.0)

Задача поиска пути с минимальным перепадом энергии (в англоязычной литературе – minimum energy path ) возникает при исследовании различных химических и физических процессов, которые включают в себя переход из одного состояния в другое. Длительную эволюцию физической системы можно охарактеризовать переходами между энергетическими минимумами на поверхности потенциальной энергии [1]. В рамках теории переходных состояний энергетический барьер между минимумами определяет скорость перехода.

Примером численного метода, результаты применения которого существенным образом зависят от процедуры поиска путей с минимальным перепадом энергии, является кинетический метод Монте-Карло [2]. Теоретической основой метода является теория переходного состояния [3]. При моделировании физическая система движется в направлении наименьшей полной энергии по пути с наименьшими энергетическими барьерами к термодинамическому равновесию. Метод включает в себя два основных этапа: составление базы данных энергетических барьеров между различными состояниями, которые определяют так называемые события, и процедуру выбора одного из возможных событий. При составлении базы данных ставится рассматриваемая в работе задача.

Следует отметить, что теория переходного состояния имеет ограничения, которые делают её напрямую неприменимой к изучению некоторых процессов. Например, процесс образования белок-белок комплекса включает в себя большое количество сложных взаимодействий [4], в которых трудно выделить фиксированные переходные состояния на протяжении всего времени течения процесса ассоциации компонент комплекса (в отличие от некоторых химических реакций). Помимо этого, в биологических системах молекулы находятся в постоянном тепловом движении, что затрудняет применение статических методов.

Несмотря на указанные замечания, основные принципы теории переходного состояния могут быть адаптированы и применены для моделирования различных макромолекулярных процессов. При этом задача поиска пути с минимальным перепадом энергии актуальна и рассматривается в различных исследованиях [5].

Постановка задачи

Определяемую функцией V(x 1 ,...,x n ) : М^М поверхность будем называть поверхностью потенциальной энергии, считая что она определяет соответствующий физической системе энергетический ландшафт, который представляет собой отображение возможных состояний системы. Стационарные точки функции определяются решением уравнений вида cV/cx , = 0. По числу отрицательных собственных значений Гессиана функции в стационарной точке H , = 8 2 V/8x i 8x j можно выполнить их классификацию: локальный минимум определяется отсутствием отрицательных значений; присутствие одного отрицательного значения указывает на седловую точку (за исключением специальных случаев [1]).

Предположим, что у рассматриваемой функции V есть не менее двух локальных минимумов ( M 1 и M 2 ) и одна седловая точка S . Путь с минимальным перепадом энергии - это кривая у : [0;1] ^ ^ с началом в точке M i и концом в точке M 2 , которая проходит через седловую точку S, и в любой точке этой кривой касательная параллельна градиенту V, за исключением стационарных точек. Строгое определение пути, как непрерывного отображения отрезка в топологическое пространство, а также исследование его устойчивости представлено в работе [1].

Необходимо отметить, что, поскольку в работе будет рассматриваться нахождение пути численным методом, выражение кривой представляется не аналитическим уравнением, а множеством точек, каждая из которых соединена отрезками с последующей точкой на этом пути. Такое представление пути позволяет визуализировать его как последовательность точек, чередующихся с отрезками, которые соединяют эти точки и определяют форму кривой.

С точки зрения химической кинетики переходное состояние определяется точкой, которая имеет наибольшее значение потенциальной энергии среди всех точек на пути. В случае простейших реакций в этой точке переход между двумя различными состояниями системы наиболее вероятен. При наличии нескольких седловых точек на пути, переходное состояние будет определяться седловой точкой с наибольшим значением.

Следует отметить, что, если в функции присутствует несколько минимумов и седловых точек, возможно построение нескольких путей, которые соединяют начальную и конечную точки, каждый из которых будет удовлетворять представленному выше определению пути. В таком случае, каждый путь является путем с минимальным перепадом энергии. Из множества различных путей возможно выделение единственного в соответствии с определенным критерием. Например, выбрать путь с наименьшим по величине барьером или по числу встречаемых узловых точек. Как правило, выделение конкретного пути формулируется как отдельная задача.

Метод эластичной ленты

Метод эластичной (упругой) ленты [6] (в англоязычной литературе - nudged elastic band) - один из популярных методов, впервые представленный для поиска пути реакции в модельной системе, состоящей из трех атомов, которые могут двигаться вдоль линии. Рассматриваемый метод является одним из методов «цепочки состояний». В таких методах путь представляется множеством состояний (авторы используют термин images ), которые связываются друг с другом в цепь с использованием «пружинок». Чтобы избежать путаницы в понятиях, далее «звенья» этой цепи будем называть вершинами. Каждая вершина характеризуется точкой в пространстве и набором сил: потенциальной и упругих от соседних состояний. Изначально вершины распределяются на поверхности потенциальной энергии. В процессе работы метода цепочка вершин релаксирует к пути с минимальным перепадом энергии. При этом упругие силы не позволяют соседним вершинам значительно приближаться или растягиваться по поверхности.

Обозначим вершины как R i ( i=1,...,N) , где N - число всех вершин в цепи. Суммарная сила F i , действующая на вершину R i , определяется следующим образом:

F i = - grad VR) + S i , S i = к ( R i+i - R i ) - k(R - R -i ), где V(R i ) - значение потенциала в точке R i , S i - сумма упругих сил, к - упругость пружинки. Упругие силы влияют на проекцию силы F_i , поэтому из них достаточно извлечь только тангенциальную составляющую. Определяя шаг и рассматривая в потенциальных силах только перпендикулярную составляющую, множество состояния будет смещаться к положению искомого пути. Кратко работа метода представлена на рис. 1. Детали получения составляющих каждой из сил приведены в работе [7].

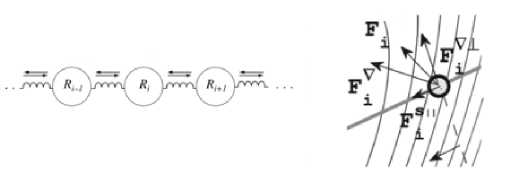
Рис. 1. Слева: схематичное представление цепочки вершин.

Справа: составляющие силы, действующей на вершину в двумерном случае

Методы поиска пути с минимальным перепадом энергии можно условно разделить на два класса: методы, в которых требуется знать начальное и конечное состояние системы, и методы, в которых знать конечное состояние системы не требуется. Представленный метод позволяет как фиксировать начальную и конечную вершину, так и оставлять свободными. Таким образом концевые вершины цепи в процессе работы метода могут уточнить локальные минимумы, в области которых они изначально представлены.

В качестве критерия сходимости метода обычно выступает значение суммы всех сил между вершинами. Таким образом, в методе происходит минимизация этой суммы, и поиск считается завершенным, когда сумма сил становится ниже заданного порогового значения.

Следует отметить, что путь между начальной и конечной вершиной разбивается на фиксированное количество вершин, то есть метод является дискретным. При этом потенциальную функцию и градиент требуется вычислять на каждом шаге метода для каждой вершины. Для этого этапа (помимо параллелизации) предложено значительное количество модификаций метода [8], включая использование различных локальных оптимизаторов [9]. Необходимо отметить, что метод в значительной степени зависит от коэффициента упругости пружинок k, для которого в общем виде выбор значения предложен авторами метода [6, 7].

При использовании метода в задачах высокой размерности возможно «запутывание» пути. Как правило, вершины цепи распределяется равномерно от начальной вершины к конечной. Например, вдоль прямой с равным шагом. При сложном энергетическом ландшафте возможно попадание в глубокие локальные минимумы со значительным отклонением от «направления» изначального пути, а поскольку «изгиб» пути в методе не контролируется возможно значительное смещение пути. В качестве естественного решения этой проблемы предлагается модификация метода с использованием принципов из теории балок Эйлера – Бернулли, в которой учитывается упругость пружинок во всех направлениях [10].

Результаты численных экспериментов

В результате выполненной работы реализован метод эластичной ленты. Метод применен для поиска пути с минимальным перепадом энергии на модельных потенциалах, являющихся классическими демонстрационными примерами потенциалов для проведения тестов различных методов химической кинетики.

В качестве первого потенциала выбран потенциал Muller-Browns [11], который определяется следующим образом:

V (х,у) = ^=1 A teaiCx-xi)2 +b^x-x)((.y-y?')+ci(.y-y?')2, где A = [–200, –100, –170, 15], a = [–1, –1, –6.5, 0.7], b = [0, 0, 11, 0.6], c = [–10, –10, –6.5, 0.7], x0 = [1, 0, –0.5, –1], y0 = [0, 0.5, 1.5, 1]. На рассматриваемой области потенциал имеет два локальных минимума, один глобальный и две точки перегиба. В вычислительном эксперименте начальная и конечная вершины располагались в локальном и глобальном минимуме. Остальные 48 вершин были расположены на соединяющем минимумы отрезке с равным шагом. В результате применения метода был найден путь, проходящий через седловые точки. На рис. 2 представлен начальный и конечный путь и, выражаясь в терминах химии, профиль реакции, где номер вершины представляет собой координату реакции. Начальная вершина представлена в локальном минимуме, поэтому на контурном графике путь проходит справа на лево.

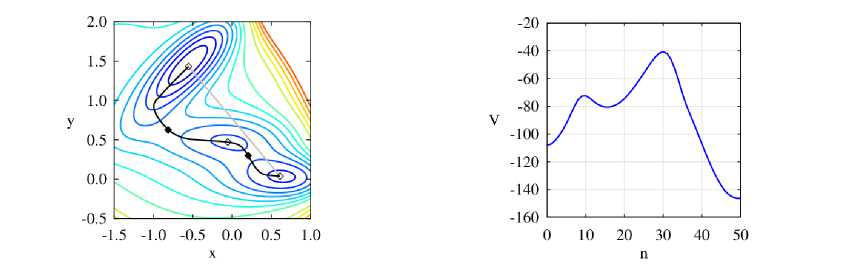
Рис. 2. Слева: начальный и найденный путь на контурном графике потенциала. Точками отмечены седловые точки потенциала. Справа: профиль значений найденного пути

Вторым потенциалом выбран потенциал Wolfe-Quapp [12, 13], который определяется следующим образом:

У (%, у) = %⁴ + у⁴ — 2%² — 4у² + %у + 1^ + ^.

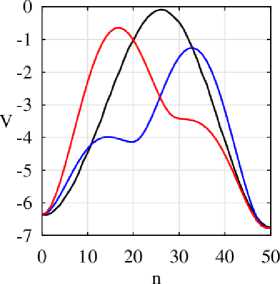
В отличие от первого потенциала на рассматриваемой области присутствуют два локальных минимума, один глобальный минимум и три седловых точки. В зависимости от начального положения 50-ти вершин, которые отмечены на рис. 3 серыми отрезками, путь может быть проложен через одну (отмечен красным цветом) или две седловые точки, включая один минимум (отмечен синим цветом). В третьем случае начальный путь соединял глобальный и локальный минимумы, но из-за большого значения коэффициента упругости путь не достиг седловых точек и локального минимума.

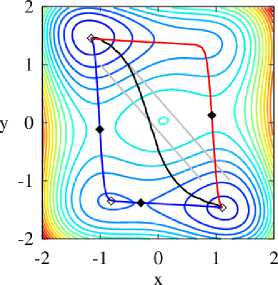
Рис. 3. Слева: найденные пути на контурном графике потенциала.

Точками отмечены седловые точки потенциала. Справа: профили найденных путей

Заключение

В результате выполненной работы рассмотрен метод эластичной ленты и приведены результаты численных экспериментов для двух потенциалов. Продемонстрирована высокая чувствительность метода к входным параметрам. Несмотря на указанные в работе недостатки метода, в настоящее время исследователи предлагают различные модификации метода и вариации его использования. Например, в работе [14] предложен один из вариантов реализации метода для популярного пакета молекулярной динамики AMBER с использованием вычислений на графических процессорах. Для упомянутой проблемы «запутывания» пути исследователями в [15] предлагается гибридный подход, который применяет метод роя частиц с построением графа возможных путей, что делает возможным провести финальную классификацию и выявить минимальный путь.

В качестве направления дальнейших исследований выступает рассмотрение метода на задачах высокой размерности, а также реализация существующей модификаций метода [10].