Применение метода когерентного накопления в вихретоковом контроле параметров дисперсных сред

Современное развитие авиационной и космической техники связано с увеличением ресурса и повышением надежности всех основных систем технических объектов и изделий в целом. Условия эксплуатации современных изделий авиационной техники (АТ) связаны с высоким уровнем динамических нагрузок и внешних воздействий, что предопределяет использование конструкций и агрегатов ограниченного ресурса, техническое состояние которых должно контролироваться постоянно или периодически.

Использование в современной авиационной и космической технике, а также других отраслях промышленности жидкостных систем различного назначения влечет за собой проблему контроля их технического состояния, в особенности агрегатов, содержащих узлы трения (насосы, гидроцилиндры и т.п.).

и т.д. Это обуславливает необходимость контроля не только количественного, но и качественного состава частиц износа в рабочей жидкости, т.е. необходимость различения материала частиц загрязнений.

Для оценки концентрации и гранулометрического состава металлических частиц износа в жидкости гидравлических систем перспектив-но применение средств электромагнитного (вихретокового) контроля (ВТМ), т.к. он позволяет контролировать наличие в рабочей жидкости металлических частиц износа, причем можно определять материал частицы по обобщенному параметру ЦО , где Ц - относительная диэлектрическая проницаемость материала частицы, а О - удельная проводимость [2]. Фактически это дает возможность идентифицировать в рабочей жидкости частицы узлов агрегатов, изготовленных из стали или ее сплавов, и частицы цветных металлов и сплавов. С учетом того, что контроль частиц износа соответствующих узлов трения гидроагрегатов осуществляется в замкнутой гидросистеме, такая возможность различения материала частиц является мощным диагностическим признаком при контроле технического состояния жидкостных систем.

С целью повышения разрешающей способности вихретоковых преобразователей (ВТП) авторами предложена усовершенствованная конструкция ВТП, позволяющая реализовать метод когерентного накопления сигнала [3]. Структурная схема предлагаемого ВТП приведена на рис. 1.

Данный метод улучшает отношение сигнал/ шум на выходе ВТП. При возбуждении всех обмоток ВТП от одного источника тока, а также при условии ламинарности потока жидкости внутри чувствительного объема датчика можно ожидать одинаковых сигналов с каждой из обмоток от одной и той же частицы. При этом шумы в разных обмотках (каналах измерения), очевидно, статистически независимы. В этом случае когерентное

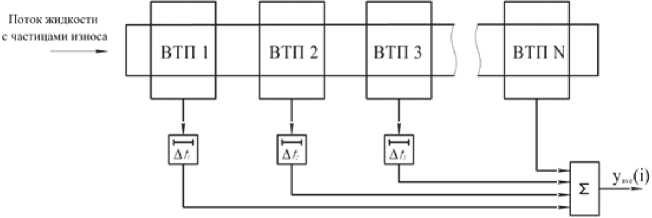
Рис. 1. Структурная схема ВТП

усреднение сигналов с разных обмоток от одной и той же частицы позволит повысить отношение сигнал/шум.

В работе [4] показано, что при равных условиях (одинаковой модели сигнала и помех, а также количества усредняемых реализаций смеси сигнала с помехами) по критерию коэффициента улучшения отношения сигнал/шум при цифровой обработке сигналов, наблюдаемых на фоне аддитивных и мультипликативных помех, эффективность усреднения сигналов во временной области выше эффективности усреднения сигналов в частотной области как при усреднении результатов быстрого преобразования Фурье, так и быстрого вейвлет-преобразования.

Ввиду того, что при вихретоковом анализе информационными параметрами являются как амплитуда, так и фаза сигнала, метод когерентного накопления (известный также как метод преддетекторного, линейного или векторного усреднения [5]) является более предпочтительным по сравнению с методом некогерентного накопления. При некогерентном накоплении (известном также как среднеквадратичное, последетек-торное или скалярное) происходит усреднение отсчетов сигнала в случае, когда на временные соотношения дискретизации не накладываются никакие ограничения, т.е. интервалы измерения сигнала никак не синхронизированы с фазой измеряемого сигнала. При этом усреднение множества наборов отсчетов “размазывает” полезный сигнал по набору отсчетов, при этом теряется возможность измерять фазу вносимого в ВТП напряжения.

Метод когерентного усреднения подразумевает равенство начальных фаз усредняемых сигналов. Для обеспечения синфазности усредняемых сигналов с различных обмоток применяется корреляционный анализ, позволяющий определить, какую точку в общей форме сигнала взять за точку отсчета. Под точкой отсчета подразумевается величина временной задержки, определяемая временем перемещения частицы износа от одной обмотки датчика до другой. При этом предполагается, что максимум основного всплеска на корреляционной функции является статистически устойчивым. Однако наличие большого коли- чества влияющих факторов, а также низкое отношение сигнал/шум приводит к искажению формы взаимной корреляционной функции (ВКФ) сигналов с различных измерительных обмоток ВТП. Так, возможно перемещение положения максимальной амплитуды, либо наличие нескольких, близких по величине экстремумов ВКФ. В работе [6] показано, что использование при обработке ВКФ “центра тяжести по энергии” позволяет обеспечить наиболее точную оценку положения точки отсчета, необходимого для применения метода когерентного накопления. Однако и в этом случае относительная ошибка определения положения точки отсчета может составлять до 7% [6].

В связи с этим, необходимо произвести оценку влияния ошибки определения точки отсчета на эффективность когерентного накопления сигнала и, как следствие, на оценку параметров частиц износа.

Для анализа возьмем сигнал дифференциального вихретокового датчика, полученный в результате моделирования системы “датчик-частица износа” методом конечных элементов в программном комплексе Ansoft Maxwell 15.0 на суперкомпьютере “Сергей Королев” (рис. 2).

Параметры моделирования приведены в табл. 1.

Определим совокупность задержек сигнала, возникающих при движении частицы по каналу ВТП. Для анализа влияния величины задержки на эффективность когерентного накопления будем варьировать среднеквадратичное отклонение величины задержки. Величину вариации выберем, исходя из характерных размеров ВТП и профиля распределения скоростей в канале ВТП (рис.3)

Профиль скоростей, приведенный на рис. 3, получен для канала ВТП цилиндрической формы диаметром 1мм. Скорость движения частиц износа максимальна на геометрической оси канала и составляет 2.8 м/с. При изменениях скорости в канале ВТП в пределах 10% [1] и среднем расстоянии между соседними измерительными обмотками ВТП 10мм диапазон вариации положения фронта импульса на временной оси находится в пределах 3,25..3,97мс.

Рис. 2. Сигнал с дифференциального ВТП

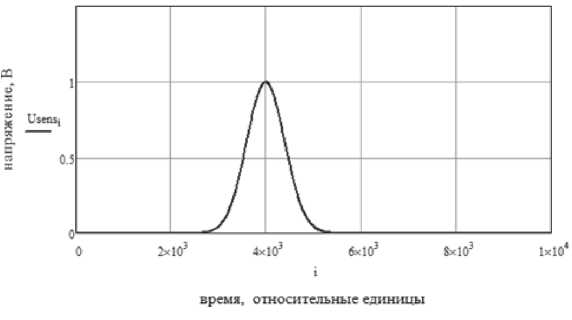
Таблица 1. Параметры моделирования ВТП

Параметр	Значение
Материал час тицы	медь
Форма частицы	шар
Диаметр частицы, мкм	90
Частота возбуждающего сигнала, МГц	10

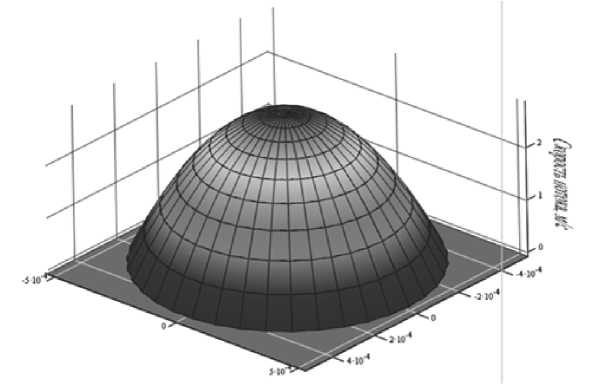
Рис. 3. Профиль скорости жидкости в канале ВТП

При моделировании будем полагать, что смещение фронта импульса подчиняется нормальному закону распределения. Математическое ожидание величины смещения примем равным 0с. При этом величину среднеквадратичного отклонения (СКО) смещения будем задавать из диапазона 0...0,4 мс.

На рисунке 4 приведено распределение задержек фронта импульса для среднеквадратичного отклонения равного 0с. Закон распределения нормальный.

Как показано в работе [по накоплению], целесообразно использовать ВТП с 10…20 измерительными обмотками. Примем количество измерительных обмоток равным 20. Таким образом, количество импульсов для когерентного усреднения в каждом из наборов составит 20.

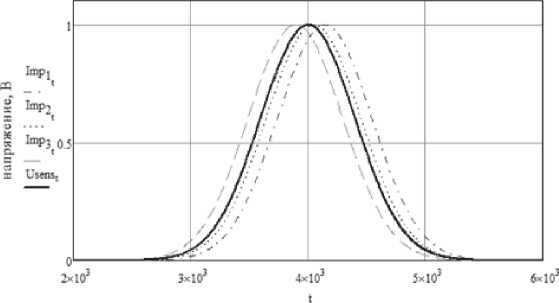
На рис. 5 приведены три из двадцати импульсов Imp1(t), Imp2(t), Imp3(t), образовавшихся в результате смещения искомого сигнала Usens(t). Видно, что смещение импульса по временной оси происходит как в положительную, так и в отрицательную стороны относительно исходного положения.

Когерентное накопление двадцати импульсов для каждого из возможных значений СКО смещения позволяет получить набор результирующих импульсов с ВТП. На рисунке 6 приведены искомый импульс Usens(t), а также три импульса Imp_coh1(t), Imp_coh2(t), Imp_coh3(t) (из возможных двадцати), полученных в результате когерентного накопления сигналов с измерительных обмоток ВТП.

Из рис. 6 видно, что при когерентном усреднении импульсов, фронты которых смещены по времени друг относительно друга, возникает ошибка накопления. При малых значениях СКО смещения когерентно накопленный импульс Imp_coh1(t) совпадает с искомым импульсом Usens(t). С ростом СКО смещения начинает уменьшаться амплитуда когерентно накопленных импульсов и появляется дополнительное смещение по фазе – Imp_coh2(t).

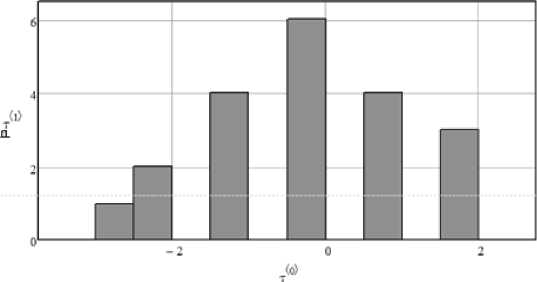
величина отклонения, относительные единицы

Рис. 4. Смещение фронта импульса

время, относительные единицы

Рис. 5. Импульсы с различных измерительных обмоток ВТП

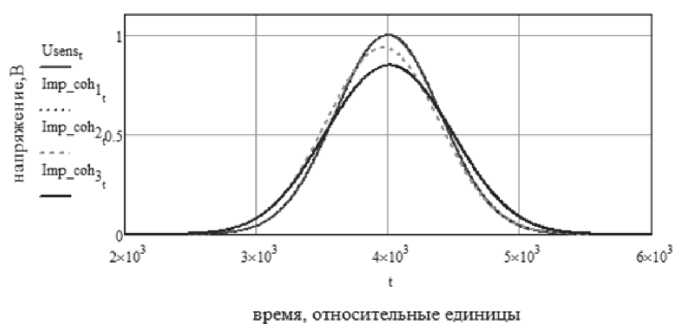
Рис. 6. Искомый импульс Usens(t) и набор из когерентно усредненных импульсов

При максимальных значениях СКО амплитуда когерентно накопленного импульса Imp_coh3(t) составляет не более 80% от амплитуды искомого импульса Usens(t).

Для оценки расхождения формы искомого сигнала и когерентно накопленных сигналов воспользуемся парным коэффициентом корреляции (взаимно корреляционной функцией ВКФ). ВКФ может быть вычислена по формуле [6]:

n

^ ( Usens i - Usens ) ■ (Im p _ coh i - Im p _ coh )

r = ,    i =1                     ,                          =

n

n

^ (Usens i - Usens ) ² ■ 1^ (Im p _ coh i - Im p _ coh ) 2 i = 1                                              i = 1

На рис. 7 приведена функция Fcorr(t) равная

Fcorr t = 1 - r t . (2) где r_t – величина ВКФ для разных значений СКО смещения импульса.

Из рис. 7 видно, что парный коэффициент корреляции близок к единице. Т.к. r > 0,95 для всех значений СКО, то в соответствии с [7] все когерентно накопленные импульсы и искомый импульс являются отлично коррелирующими функциями.

Таким образом, рассматриваемый диапазон смещений сигналов с измерительных обмоток ВТП не оказывает значимого влияния на форму и положение на временной оси искомого импульса при когерентном накоплении сигналов.

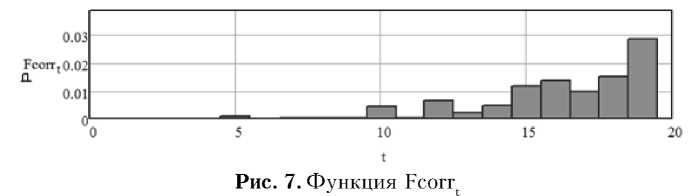
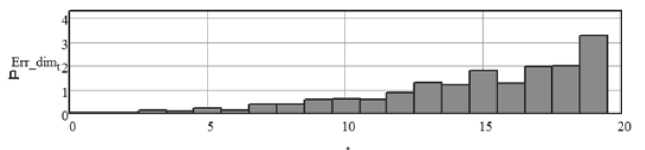
Рис. 8. Относительная погрешность измерения размера частицы износа

На рис. 8 приведена оценка относительной погрешности измерения характерного размера частицы износа, возникающая при когерентном накоплении смещенных импульсов.

Видно, что с ростом переменной t (с увеличением СКО смещения импульса) растет величина относительной погрешности. Нелинейный характер функции Err_dimt обусловлен нелинейной зависимостью между размером частицы износа и величиной вносимого в ВТП напряжения. При этом максимальная относительная погрешность составляет 3.2% при СКО смещения импульса равном 0,4мс.

Таким образом, для многообмоточного ВТП с диаметром канала 1мм при изменениях скорости течения жидкости в канале ВТП в пределах 10% от максимальной (2,8м/с) относительная

погрешность определения размера частицы износа с характерным диаметром от 90мкм и выше при использовании метода когерентного накопления составляет не более 3.2%. При этом практически не искажается форма импульса с измерительной обмотки ВТП, а также его положение на временной оси.

• 6.

• 7.