Применение метода конечных элементов для расчёта электромагнита тормоза инвалидной коляски

Рассмотрены вопросы применения метода конечных элементов при решении осесимметричных задач теории поля на примере электромагнитного тормоза для инвалидной коляски.

Во многих технических устройствах очень широко применяются электромагниты для выполнения функций, основанных на притяжении подвижной системы (якоря) электромагнитом. В связи с этим, встают вопросы более точного расчета данных устройств и в особенности его тяговой характеристики.

Как известно, сила тяги электромагнита равна частной производной энергии по перемещению:

dx где W„ - энергия магнитного поля, исследуемой системы;

х - координата перемещения.

Сила Р направлена таким образом, чтобы якорь стремился приблизиться к электромагниту. При этом энергия, запасенная в магнитном поле воздушного зазора, переходит в механическую работу, затрачиваемую на перемещение якоря.

В данной работе рассматривается вопрос расчета силы тяги электромагнита, изображенного на рис. 1.

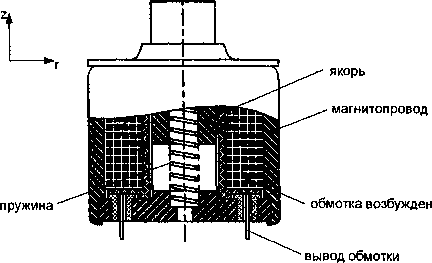
Рис. 1. Общий вид электромагнита

Расчет произведен двумя способами. Первый основан на классическом подходе, рассмотренном в [1].

В данном случае изменение энергии магнитного поля рассматривается только в воздушном зазоре, не учитывается изменение энергии всей магнитной системы и поле рассеяния между якорем и магнитопроводом является плоскопараллельным. Данные допущения, по мнению авторов, является недостаточно точными, так как при перемещении якоря электромагнита имеются участки магнитной системы с насыщением и распределение магнитного поля имеет более сложный характер, что заметно может сказаться при расчете усилия.

По этому, предлагается расчет исследуемого электромагнита (см. рис. 1) на основе метода конечных элементов (МКЭ). Как известно, исследуемая область в МКЭ разбивается на конечные элементы различной конфигурации. В данном случае дискретизация пространства произведена с использованием треугольных элементов второго порядка, что повышает точность решения задачи. Условия симметрии позволяют ограничиться рассмотрением половины исследуемой области электромагнита.

Интерполяционный полином для квадратичного треугольного элемента осесимметричной задачи имеет вид:

и = a, +ct₂r + а₃г + а₄г² + a₅rz + «₆z², (1)

где г - расстояние от оси симметрии до узлового потенциала;

z - ось симметрии.

При расчете осесимметричной задачи необходимо решить уравнение Пуассона в виде:

Вг

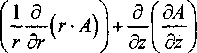
= ц-J,

где А - векторный магнитный потенциал;

J- вектор плотности тока;

ц - магнитная проницаемость среды.

При введении другой переменно Т = г ■ А данное уравнение принимает симметричный вид относительно производных по координатам г и z [2]:

—--+—--\ = J,           (3)

dr ( r 8r J dz\ r dz J

1 где v = --магнитная проводимость среды.

В

Составляющие магнитных индукций по осям примут вид:

„    1 d'P „ 1 dP г dz г dr

С учетом выше изложенного решение уравнения (3) связано с минимизацией функционала:

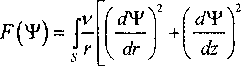
Д-Зр-Ч'Д (5)

или с учетом (4):

F^ = jv-r-B²ds-2 jd-Pds,        (6)

5                 8

где В = ^В² + В² - значение индукции в элементе.

Система уравнений, для решения задачи, получается из условия стационарности функционала du

Коэффициенты матриц, получаемых при расчете производных, входящих в уравнение (5), имеют вид:

„ f du, du. du, du ) r^dr dr dz dz J

C; = -2 ^J-a,dse, s, здесь ^, Uj - базисные функции, являющиеся полиномами переменных г и г с коэффициентами а,.

Далее формируется глобальная матрица и вектор столбец правых частей. После этого, любым из известных способов производят решение системы линейных уравнений для каждой итерации до сходимости итерационного процесса.

Решение осесимметричной задачи для электромагнита, изображенного на рис. 1 представлено на рис. 2 при фиксированном воздушном зазоре.

z А

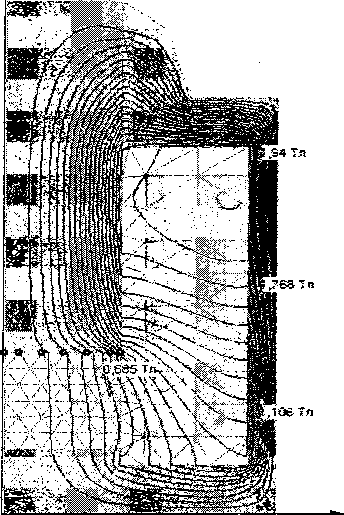
Рис. 2. Распределение магнитного поля

г

МКЭ позволяет достаточно полно исследовать данный объект при различных изменениях как магнитной системы, так и электрических параметров.

' На рис. 3 представлена зависимость тяговой характеристики исследуемого электромагнита от величины воздушного зазора F = /().

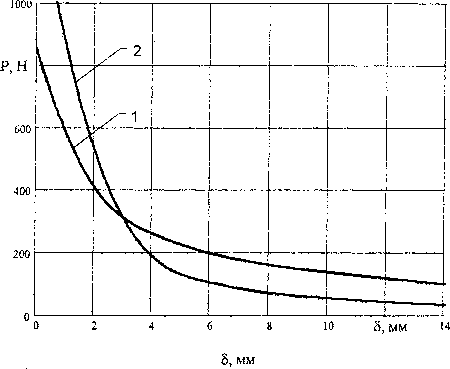
Рис. 3. Тяговые характеристики электромагнита: 1 - механическая характеристика электромагнита, рассчитанная методом конечных элементов; 2 - механическая характеристика электромагнита, рассчитанная аналитически

На рис. 4 представлена зависимость тягового усилия исследуемого электромагнита от магнитодвижущей силы (МДС) Р = /(F^ при фиксированном воздушном зазоре.

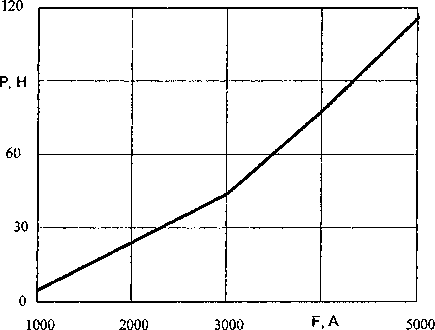
Рис. 4. Зависимость тягового усилия от МДС обмотки