Применение метода крупных частиц при описании развития взрыва газо-воздушной смеси в незамкнутых объёмах

Моделирование горения газовых смесей имеет ряд особенностей, существование которых обусловлено методом, взятым за основу моделирования. Разработанный Ю.М. Давыдовым метод крупных частиц является одним из наиболее современных методов построения моделей для численных экспериментов в области динамики непрерывных сред. Метод позволяет решать задачи при отсутствии априорной информации о виде решения. Авторами предложена модификация метода крупных частиц, позволяющая распространить его на задачи распространения пламени в газообразных средах.

Работа проведена при содействии Российского фонда фундаментальных исследований.

Авторами решается задача о моделировании процессов горения смесей газообразных топлив в объемах произвольной геометрии. Решение этой задачи позволит в частности производить анализ конструкций топок, работающих на газе, на взрывобезопасность еще на стадии проектирования [1].

Решение задачи предусматривает моделирование динамики двух разделённых газовых сред, взаимодействующих во фронте горения. В модели учитывается влияние ограждения объема, в том числе и возможность его разгерметизации. Задача решается в трёхмерной постановке.

Авторами принимаются следующие допущения, касающиеся моделируемых сред:

• 1)    исходная смесь газ-воздух является однородной;

• 2)    различие термодинамических характеристик исходной смеси и продуктов сгорания является незначительным;

• 3)    реакция горения протекает на границе несгоревшей смеси и продуктов сгорания – во фронте горения.

С учетом указанных допущений задача сведена к моделированию динамики среды с едиными свойствами на основе одного из существующих методов решения многомерных нестационарных задач механики сплошных сред. Выбор конкретного метода ограничен произвольностью геометрии расчетной области, а так же возможностью наличия особенностей в моделируемых течениях.

Материалы и методика исследований

В качестве базового метода авторами работы был выбран метод крупных частиц [2], [3]. Метод крупных частиц позволяет по единому алгоритму исследовать сложные задачи обтекания тел различной формы в широком диапазоне изменения начальных условий при наличии различных особенностей течений. Метод относится к группе методов «частиц в ячейках», но также использует механизмы, свойственные эйлеровым методам. Основная идея метода крупных частиц состоит в расщеплении исходной системы уравнений по физическим процессам, что позволяет модифицировать метод для учета дополнительных процессов.

В методе крупных частиц для описания динамики газодинамической системы используется система уравнений Эйлера в дивергентной форме (1), замыкаемая уравнением состояния (2) [3]:

»⁺ div^{( p U} ) = 0;

^x + div (pUxU) + -p = 0; о t dpU v j       + div(pUyU) + -p = 0;

d t

^ U  + div ( p UU) + ^d p = 0;

d t

+ div ( p EU ) + div (pU ) = 0;

L d t p = pl (y -1);

I = E -

U ²

U² = U_x ² + U ,² + U _z²; xyz где p - плотность газа, кг/м3;

U – вектор скорости, м/с;

E – удельная полная энергия, Дж/кг;

• p – давление, Па;

• / - показатель адиабаты среды;

I – удельная внутренняя энергия, Дж/кг;

U x , U y , U z , – составляющие вектора скорости, xy z

соответственно, вдоль осей x , y , z , м/с.

На область интегрирования накладывается эйлерова (фиксированная в пространстве) расчетная

сетка, состоящая из

Лг сторонами x

заменяется системой из

прямоугольных ячеек со ^А z . Моделируемая среда жидких частиц, совпадающих

в данный момент времени с ячейкой эйлеровой сетки. Процесс вычислений состоит из многократного повторения шагов по времени. Расчет каждого временного шага (вычислительного цикла) в свою очередь разбивается на три этапа:

1. «эйлеров» этап, когда пренебрегается всеми эффектами, связанными с перемещением жидкости (потока массы через границы ячеек нет); здесь на фиксированной эйлеровой сетке определяются

промежуточные значения искомых параметров потока

( U ~ x , U ~ y

U ~ z , E ~ );

2.   «лагранжев»   этап,   где вычисляется

плотность потока массы при движении жидкости через границы эйлеровых ячеек;

3. заключительный этап — определяются

, P U окончательные значения параметров потока ( , x , UU y , z , E ) на основе законов сохранения массы, импульса и энергии для каждой ячейки и всей

системы в целом.

На первом этапе изменяются лишь величины, относящиеся к ячейке в целом, а жидкость предполагается моментально замороженной. Поэтому конвективные члены вида div ( фр U ) где ф = {1, U x , U y , U z , — } , соответствующие эффектам перемещения, в уравнениях (1) откидываются. Тогда из уравнения неразрывности следует, что поле плотности будет «заморожено» и исходная система (1) здесь примет вид (3):

На втором этапе моделируется движение потока массы ^{A M} через границы эйлеровых ячеек и происходит перераспределение частиц по пространству. При этом полагается, что вся масса переносится только за счет нормальной к границе составляющей скорости. Значения A M возможно определять по формулам первого порядка точности (6): ~~

Pi,j, kU 1 AyAz At, U , xi+2, j, k                  xi+2, j, k;(6)

~~

Pi+1,j,kU 1 AyAzAt, U 1

x i +~, j , k                     x i +~, j , k

A M .    = ^

i ⁺ _? j , к

<

P	d U x	+ ^ p = 0;
	d t	d x
P	d U y	+ ^ = 0;
	d t	d y
	d U	d p
P		+ —= 0;
	d t	d z

Явные

- р - + div (pS) = 0; d t

конечно-разностные аппроксимации

первого порядка точности по времени и пространству

для (3) будут выглядеть как (4), (5):

~

U x i , j , k

= U xi, j , k

^^^^^^^B

^p + 1.1k

V 2

^^^^^^^B

^Pi - 2.j.k )

A t   ;(4)

P i , j , k ^{A x} ’

~~ аналогично для Uyi,j,k и Uzi,j,k

~

—  = —  — i, j,k           i, j,k

p 1 ^U 1    ^— p 1 ^U 1

i +—, j , k xi +—, j , k        i — —, j , k xi — —, j , k

^{— p} 1 ^U 1

i ^, j ^— 2. ^k    y i ^, j ^— 2. ^k

+

+

p ₁ U ₁

i ^, j ⁺ 2. ^k yi ^, j ⁺ 2. ^k

A y

+

p 1 ^U 1 ^— p 1 ^U 1

i , j , k +—     z i , j , k +—         i , j , k ——     z i , j , k ——

A z

A t

;

P i,j, k

Величины с дробными индексами, относящиеся к границам ячеек, равны полусумме значений соответствующих параметров в соседних ячейках.

P i , j , k ⁺ p i + 1, j , k

Например, p .     =--------------- и так далее.

i + 2, j , k               2

Аналогично для A M  1 и A M   1 .

i , j + ^, k            i , j , k + 2

Приведенные формулы позволяют проводить устойчивый счет без введения явных членов искусственной вязкости. Устойчивость вычислений обеспечивается при этом внутренней структурой разностной схемы — наличием аппроксимационной вязкости.

На третьем (заключительном) этапе проводится регуляризация сетки (пересчет сдвинувшейся сетки в прежнее состояние), происходит перераспределение массы, импульса и энергии по пространству и определяются окончательные поля эйлеровых параметров потока в момент времени t ” ^{+ 1} = t ” + A t . Уравнения этого этапа представляют собой законы сохранения массы M , импульса P и полной энергии E , записанные в разностной форме:

F ” ^{+ 1} = F ” +^ F ”        (7)

р, где F = {M, P^, —}.

Эти уравнения утверждают, в частности, что внутри поля течения нет источников и стоков M , P и ^— , а их изменение за время A t осуществляется только за счет взаимодействия на внешней границе области течения. При этом предполагается, что потоки массы через границы ячеек A M , определяемые на втором этапе, несут с собой промежуточные значения скорости и удельной энергии, вычисленные на первом этапе (величины ^{A M} играют здесь роль весовых функций).

Исходя из этого, окончательные значения параметров потока на следующем временном слое вычисляются по формулам (8–10).

P

n + 1

i , j , k

A M 1 —A M 1 +A M 1 —A M 1 +A M 1 —A M 1 i —, j , k i +—, j , k i , j —, k i , j +—, k i , j , k — i , j , k +— _{: р} n +       2 __________ 2    2 _________ 2 _________ 2            2

i , j , ^k                                        A x A y A z

где

XL ^Pи k +------ i, j,k i, j,k

i , ^{j -} 2, ^k i , ^{j -} 2, ^k

~

X 1

i +;7, j , k

= <

X i , j , k ,

A M

к

~ i. j+2’k i,j+2,k

~

Y л i+1, j, k ’

x i +—, j , k

~

U 1

x i +—, j, k

> 0

X = {U x ,U y , U_z, E } .

Авторами метода крупных

—

_X ~ ₁

~

< 0(10)

частиц показано,

где

;

AE = A mRH

B ;

E„ = E + ^E = E + kBH нB

m

;

что в данной разностной схеме внутри области интегрирования имеет место строгое выполнение законов сохранения массы, импульса и энергии [3].

Граничные условия в методе крупных частиц

задаются

путем

введения

дополнительных

«фиктивных» ячеек расчетной области, параметры состояния которых определяются на каждом шаге на основе состояния соседних ячеек [2].

Для решения задач распространения пламени в газообразных средах авторами работы предложена следующая модификация метода крупных частиц [1].

Введен дополнительный параметр состояния ячейки расчетной сетки – массовая доля продуктов сгорания f . В соответствии с методом крупных частиц моделируемое пространство разбивается на совокупность ячеек. Долю продуктов сгорания f для каждой ячейки можно выразить следующим отношением

k

^B – коэффициент скорости горения смеси,

E – удельная полная энергия смеси в ячейке, Дж/кг, AE - абсолютное выделение энергии, Дж, H – теплотворная способность смеси, Дж/кг, fE н и н – соответственно, доля продуктов сгорания

и полная удельная энергия после этапа «горения».

Коэффициент скорости горения предлагается определять для каждой каждом шаге согласно выражению (17):

kB =A UB

^B A 1 ^B .

смеси ячейки

k _B

на

где

где

;

^{A 1} - характерный линейный размер ячейки сетки, м,

U

^B – нормальная скорость распространения пламени

f = mB m

.

m – общая масса смеси в ячейке, кг;

m

^B – масса продуктов сгорания в ячейке, кг.

При этом расчетные ячейки можно разделить на три группы:

в неподвижной смеси, м/с.

Для пространственных ячеек регулярной сетки характерным линейным размером является длина ребра куба ( A l = A x = A y = A z ). Существует несколько подходов к определению значения U _B как функции параметров смеси. В настоящей работе авторами принимается степенная зависимость нормальной скорости горения от относительного изменения температуры смеси [1]:

• ячейки с исходной смесью, для

которых

f < £     £ выполняется условие , где £ точности расчетов;

^u b = U B НУ

( T )e

;

–

параметр

к Tну )

«сгоревшие» ячейки –          ;

«горящие» ячейки.

где U _{B НУ}

нормальная скорость распространения

пламени в неподвижной смеси при нормальных условиях, м/с,

Моделирование

процесса

горения

T и

производится в три шага. На первом шаге рассматривается горение газа в ячейках. Для всех

A f «горящих» ячеек определяется доля газа , сгоревшего за время ^A t , и рассчитывается выделение энергии ^{A E} :

температура

^T НУ смеси

текущая температура смеси и

при нормальных   условиях,

соответственно, K, в - показатель степенной зависимости.

Текущая температура смеси может быть определена из уравнения состояния идеального газа (19):

BB

;

A f ^ = kB m

;

T = P£ PR.

;

где Ц - молярная масса смеси, кг/моль,

R – универсальная газовая постоянная, Дж/(К*моль) .

Второй шаг моделирования заключается в распространении горения на соседние ячейки. Первый и второй шаги предполагают неподвижность среды, что характерно для эйлерова этапа цикла метода крупных частиц [1].

Третий шаг заключается в массы сгоревшего газа через вычислительного

учете переноса границы ячеек

(заключительный этап метода крупных частиц). Перенос моделируется аналогично переносу остальных параметров ( U , E ) на основе формулы (9). Однако в виду специфического характера f параметра определений

применение выражений (10) для переносимых значений является неадекватным. В связи с этим, авторами предлагаются специальные формулы расчета переносимых значений

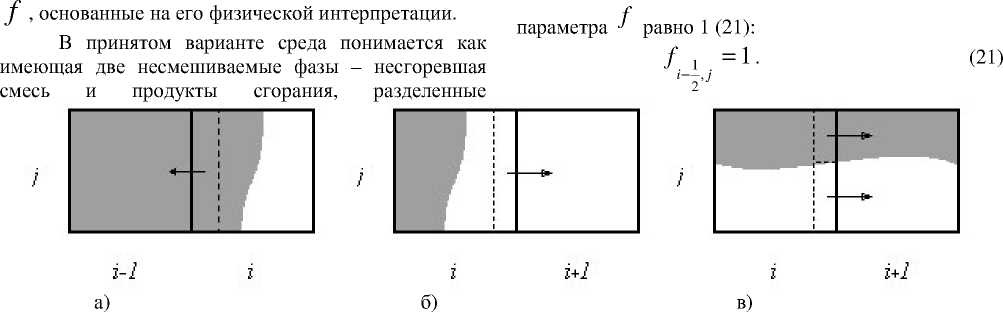
Рисунок 1 – Возможные варианты расположения фронта горения относительно границ ячеек

поверхностью фронта горения. При этом для определения значений степени сгорания f , переносимых, через границу ячейки, достаточно знать характер пересечения границы поверхностью фронта.

Рассмотрим три характерных случая (для наглядности воспользуемся двухмерной постановкой задачи).

1. Поток массы направлен из «горящей» ячейки в «сгоревшую» (20).

e < f j <  1 - e , f_i-x j> 1 - e , A M , <  0 .(20) ^i- 2’ j

В этом случае поверхность фронта не пересекает рассматриваемую границу ячейки и через границу переносятся только продукты сгорания (рис. 1.а). Это означает, что переносимое значение

2. Поток массы направлен из «горящей» ячейки в «негоревшую» (22).

e < f . <  1 - e , f_M , MM , >  0 . (22) ^{i +} 2,^j

В этом случае поверхность фронта также не пересекает рассматриваемую границу ячейки и через границу переносится только не горевшая (исходная) f смесь (рис. 1.б). Переносимое значение параметра равно 0 (23):

f 1

⁺ 2, j

^f i , j       ^fi + 1, j

.

Остальные случаи

переноса

значения

параметра f сводятся к перечисленным

выше. На

основе выражений (20-25) можно записать общие f формулы переноса для параметра :

f 1 = 0 . ^{i +} 2’ j

3. Поток массы между двумя «горящими» ячейками (24).

f 1

i +-, j , k

1,

0,

⁽ f , j , k > ^{1 - e )v( f} i + 1, j , k > ^{1 - e )};

( ^fi, j , k < f ) v

f _t + f

J i , j , k i + 1, j , k

i + 1,j , k

< e );

e <  f , j <  1 - e , e <  ^f _{M a} <  1

^^^^^^^»

e , m m 1 >  0 ^{(24) i +} ^, ^j

I 2

Использование выражений (10) для

;

формулы определения

вместо

В этом случае поверхность фронта пересекает границу ячейки. Через рассматриваемую границу переносится как исходная смесь, так и продукты сгорания (рис. 1.в). Переносимое значение параметра f равно соотношению площади границы ячейки, отсекаемой фронтом горения, к общей площади границы. Авторами работы предлагается определять это отношение как среднее арифметическое значений параметра f для двух соседних ячеек (25). Такой подход обосновывается геометрической трактовкой степени сгорания f как отношения площади (объема) ячейки, занимаемой продуктами сгорания, к общей площади (объему) ячейки.

значений параметра

переносимых

f обеспечивает адекватность

применения общей формулы переноса (9) для данного параметра.

Выражение (25) позволяет также определить условия распространения горения на соседние ячейки (второй шаг моделирования горения). Условие ( i , j , k ) «воспламенения» «не горевшей» ячейки         от

( i + 1, j , k )

ячейки            записывается в виде (27):

• f. 1 . , >  ^E .                     (27)

Результаты и их обсуждение

На основе разработанной модели авторами работы был создан программный комплекс «Вулкан-М» для моделирования горения и взрыва топливовоздушных смесей в незамкнутых объемах произвольной геометрии. С целью оценки адекватности разработанной модели, была проведена серия натурных экспериментов, результаты которых сравнивались с результатами численного моделирования.

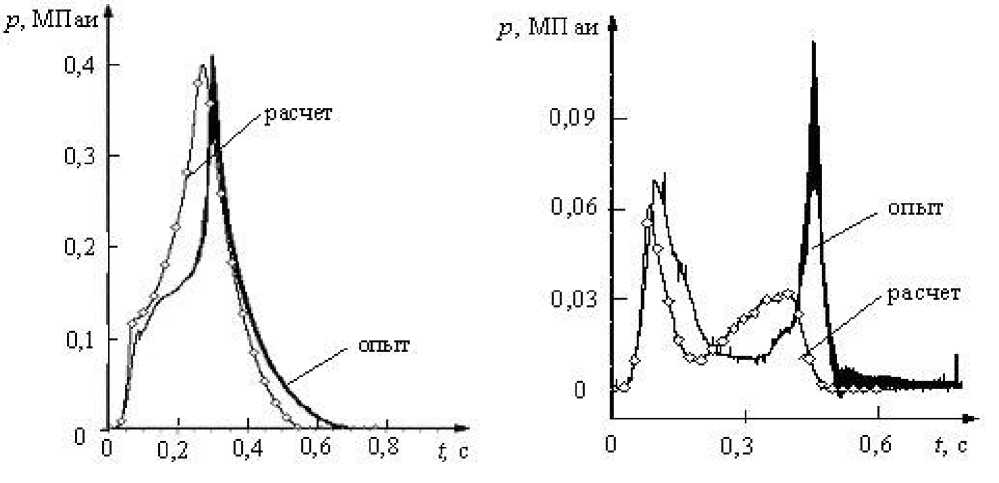
Физические эксперименты проводились на модели однопроходной цилиндрической топки (длина рабочей полости – 1500 мм, диаметр – 200 мм, объем – 4,8*10-2 м3) с тремя расположенными вдоль главной оси фланцами для моделирования различных положений взрывного клапана (рис. 2). Установка заполнялась бутан-пропан-воздушной смесью, близкой к стехиометрической. Смесь воспламенялась при помощи искрового устройства зажигания. Во время протекания взрыва регистрировались показания двух преобразователей давления, расположенных рядом с передним и задним концами установки. Эксперименты проводились как в замкнутом объеме, так и при наличии взрывных клапанов с различным диаметром проходного отверстия и различном их расположении. На рисунке 4 приведены результаты измерений давления при положении взрывного клапана в средней части установки с диаметром проходного отверстия 20 и 40 мм.

Рисунок 2 – Общий вид экспериментальной установки

Вычислительные эксперименты производились с использованием программного комплекса «Вулкан-М». Расчетная сетка состояла из кубических ячеек с длиной ребра 0.01 м. Размер сетки – 22*27*152 ячеек, из них в расчетах участвует 45504 (рис. 3). Величина шага по времени - 5 • 10 ⁷ с. Границы установки моделировались фиктивными ячейками с условиями

«непротекания». Так же на границах учитывался конвективный теплообмен между газовой смесью и корпусом установки. Взрывной клапан моделировался совокупностью фиктивных ячеек, состояние которых интерполировалось на основе параметров окружающей среды. Результаты вычислительных экспериментов приведены на рисунке 4.

Рисунок 3 – Расчетная область

(белый – расчетные ячейки, синий – фиктивные ячейки на границах, голубой – нерасчетные ячейки)

Сравнение результатов натурных и численных экспериментов показало хорошую качественную и удовлетворительную количественную адекватность модели (рис. 4). Ряд второстепенных эффектов, обнаруженных при проведении физических экспериментов, был так же получен в численных экспериментах, что говорит о высокой информативности разработанной модели и ее применимости как для решения прикладных задач, так и исследований фундаментального характера.

а)                                                               б)

Рисунок 4 – Динамика давления в полости установки (взрывной клапан на центральном фланце, диаметр проходного отверстия: а – 20мм, б – 40 мм)

а)                                                               б)

Рисунок 5 – Взрывы на экспериментальной установке (а – первый фланец, диаметр 70 мм, б – средний фланец, диаметр 40 мм)