Применение метода Лагранжа при изучении влияния модификаторов на свойства полимерных композиционных смесей

Известно, что результаты экспериментов в конкретных областях исследований принимаются на основе математической обработки.

При обработке результатов экспериментальных данных на основе определённого плана и интерполяционного подхода обосновывается достоверность исследований. Области применения интерполяции - открытие и уточнение законов природы, прогнозирование, планирование и обработка данных эксперимента, моделирование, управление различными объектами и т. п. Теория интерполяции совместно с теорией подобия и размерностей является научной основой моделирования, которое во многих случаях просто необходимо. Интерполяция может служить инструментом проверки истинности закона, полученного теоретически. Существуют различные формулы, позволяющие получить интерполяционный многочлен, одним из таких является интерполяционная формула Ньютона с применением метода Лагранжа.

Исходя из нашего исследования и полученных данных экспериментов, применили формулу Ньютона, который имеет следующий вид:

Рп (x ) = У 0 +^yr (x - x 0 ) + xy (x - x 0 Xx - xi) +... +    (x - x0 Xx - xi)-(x -

1!h            2!h2                        n!hn(1)

Воспользуемся этой формулой, как одной из возможных форм записи интерполяционного многочлена второй степени, получим:

Р2 (x ) = У 0 + ^y0 (x — x0 )+ ^yr (x - x0 )(x - xi) 1!h2!

На основе метода Лагранжа для всех составов (табл 1) получено следующее уравнение регрессии:

Р г,(г=1^10 ) =0,625X 4 -17,06x 3 +152,1x 2 -39 7,7x+805,

Пространственное изменение времени истечения составов изображено на рис 1.

Рис. 1. Пространственные изменения состава смеси

Таблица 1

Составы гетерокомпозитных материалов, рекомендуемых для применения на рабочей поверхности крупногабаритных и сложноконфигурационных оборудований

Составы и компоненты гетерокомпозитных материалов
Компоненты	1=3	CN 1=3	E	co E	co E	co co E	co U	co U	CO co О	co О
ЭД-20	100	100	100	100	100	100	100	100	100	100
ПЭПА	12	12	12	12	12	12	12	12	12	12
ГС	6	8	10	8	10	12	6	8	10	12
АКТ-10	25	25	25	30	30	30	-	-	-	-
АКС-30	-	-	-	-	-	-	15	15	10	10
Примечание: ГКТЛ-1 -гетерокомпозитные материалы с наполнителем АКТ-10 для покрытий поверхностей листовых конструкционных материалов, ГКТЗ- гетерокомпозитные материалы с наполнителем АКТ-10 для заливочных материалов сложноконфигурационных деталей; ГКСЗ- гетерокомпозитные материалы с наполнителем АКС-30 для заливочных материалов сложноконфигурационных деталей

Шаг вычисления закономерности изменения времени истечения смесей от состава гетерокомпозитных материалов:

h = x_t - х _{г I=} 360 - 350 = 10     (3)

Воспользуясь интерполяционной формулой Ньютона, для значений компонентов ЭД-20, ПЭПА, ГС и АКТ-10, составляем разностную таблицу изменения времени истечения от состава гетерокомпозитных материалов.

Разностная таблица

Таблица 2.

Время истечения x	Компоненты	Составы гетерокомпозитных материалов ГКТЛ
		y	A y	A 2 y	A 3 y
350	ЭД-20	100
			-88
360	ПЭПА	12		82
			-6		-82
370	ГС	6		0
			-6
25	АКТ-10	0

С учётом зависимости времени истечения смесей от состава гетерокомпозитных материалов имеем регрессионное уравнение (4) и его графическое изображение (рис.2) на основе интерполяцыонной формулы:

Ри„ч,«™ ( x ) =- 0,003 x ⁴ + 3,3286 x ³ - 883,318 x ² + 186030,3 x - 4068132 (4)

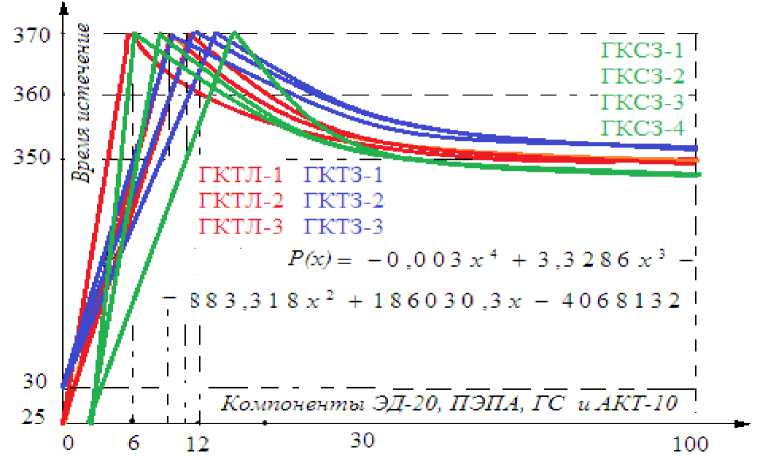
Рис. 2. Изменение времени истечения смесей от состава

гетерокомпозитных материалов

Предложено применением интерполяцыонной формулы Ньютона и метода Лагранжа с учётом реологических параметров математической обработки результатов исследования процесса структурообразования полимерных композиционных материалов и покрытий как для крупногабаритных и сложноконфигурационных технологических оборудований, так и листовых конструкционных материалов.