Применение метода наименьших квадратов для нахождения прогнозируемых значений

Автор: Е. А. Лыкова, Е. С. Лыкова

Журнал: Современные инновации, системы и технологии.

Рубрика: Электроника, измерительная техника, радиотехника и связь

Статья в выпуске: 4 (4), 2024 года.

Бесплатный доступ

Метод наименьших квадратов применяется для анализа экспериментально полученных данных. Целью данного метода является нахождение функции, которая наиболее приближенна к результатам, полученных на практике. Этот метод имеет смысл использовать при построении краткосрочного прогноза. Таким образом, необходимо пересчитывать полученные теоретически значения при поступлении новых данных. К преимуществам рассмотренного метода можно отнести относительную простоту реализации, его эффективность и универсальность. Другими словами, этот метод может быть применен в различных задачах, в которых необходимо получить предварительный прогноз, по которому можно оценить рассматриваемую систему. В ходе работы были выведены формулы по нахождению параметров, которые используются для расчета теоретических значений. Их вывод состоит в минимизации функции линейной регрессии, которая произведена путем приравнивания ее частных производных к нулю. Однако, стоит отметить, что метод наименьших квадратов позволяет найти функции только для линейно зависимых величин. Метод наименьших квадратов не используется для поиска нелинейных кривых. Более того, перед использованием метода наименьших квадратов необходимо проверить исходные значение на предмет выбросов. Под выбросами понимается значительно отличающиеся значения от общего значения.

Еще

Метод наименьших квадратов, прогнозируемые системы, параметры функции, линейная регрессия.

Короткий адрес: https://sciup.org/14131319

IDR: 14131319 | DOI: 10.47813/2782-2818-2024-4-4-0213-0222

Текст статьи Применение метода наименьших квадратов для нахождения прогнозируемых значений

DOI:

Метод наименьших квадратов – это один из методов, используемый в статистике для анализа данных. Данные метод позволяет подобрать наиболее подходящую кривую, которая бы проходила через заданные точки на числовой оси. Целью метода наименьших квадратов является минимизация суммы квадратов отклонений теоретических функций от полученных экспериментальным путем значений.

Метод наименьших квадратов применяется в различных областях [1-4]. Например, этот метод используется для решения систем уравнений, где количество неизвестных меньше числа составленных уравнений. Также метод наименьших квадратов осуществляет поиск решения в нелинейных системах уравнений. Наиболее часто метод реализует поиск функции кривой, которая проходила бы как можно ближе к значениям на числовой оси, полученным экспериментально.

К преимуществам метода наименьших квадратов можно отнести его простоту реализации. Более того, полученные данным методом оценки имеют математическое ожидание, близкое к истинному значению при любом объеме анализируемых данных. Однако надо учитывать, что построенный прогноз с использованием данного метода будет обладать достаточной точностью только для короткого периода времени [5]. Именно поэтому необходимо пересчитывать прогноз с каждым новым поступлением данных.

В ходе работы был рассмотрен процесс нахождения параметров линейной регрессии методом наименьших квадратов. В качестве эмпирических данных были взяты значения, полученные на основе работы различных точек одной марки магазина. Были рассмотрены значения товарооборота, количества продавцов и интенсивности потока покупателей. С помощью метода наименьших квадратов были получены прогнозируемые значения, по которым строится функция, наиболее приближенная к реальным значениям.

МАТЕРИАЛЫ И МЕТОДЫ

Реализация метода наименьших квадратов на основе данных различных точек одной марки магазина была произведена с использованием высокоуровневого языка программирования Python. Этот язык программирования был выбран из-за большого числа встроенных функций, которые удобны при работе с данными. Итак, с помощью встроенный библиотеки pandas возможно прочитать значение столбцов и строк из exsel файла. Код вывода исходных данных: importpandasaspd # Укажитепутьквашемуфайлу file_path = r'your_path_to_file\data.xlsx' # Чтениеданныхизфайла Excel data = pd.read_excel(file_path) # Установка параметра для отображения всех строк pd.set_option('display.max_rows', None) # Выводвсехстрок pd.set_option('display.max_columns', None) # Выводвсехстолбцов # Вывод всех данных print(data)

Для получения оценок параметров модели парной линейной регрессии необходимо минимизировать функцию, представленную формулой (1).

S(a, b) = ^^yi -a- bx^² , (1)

где n - количество всего значений, у ^ , х ^ - исходные наблюдаемые значения.

Для решения задачи по минимизации формулы (1) необходимо приравнять к нулю ее частные производные. Таким образом,

^=-2^’^,i(yl-a-bxl) = 0,(2)

^ = 2tf=1(-xiXyi-a-bzl) = 0,(3)

Из формул (2) и (3) получаем уравнения (4) и (5), из которых можно выразить параметры a и b .

EiUCy — a — bx^ = 0 ,

Т^А—хдУ —a-bx) = 0 ,

Реализуем данные уравнения на высокоуровневом языке Python для получения параметроваи b, подставляя в первом случае вместо y_j- значения товарооборота и X_j -количество продавцов, во втором случае вместо y j - значения товарооборота и X j -интенсивность потока покупателей. Прогнозируемые значения y’ можно подсчитать, используя формулу (6)

y ' = a + bx .

# Извлечение значений

y = data['товарооборот'].values x1 = data['количество продавцов'].values x2 = data['интенсивность потока покупателей'].values

# Функция для вычисления коэффициентов a и b

def calculate_coefficients(y, x):

n = len(y)

# Вычисляем необходимые суммы

# Вычисляемкоэффициентыbиa

b = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - sum_x **2)

a = (sum_y - b * sum_x)/ n

return a, b

# Рассчитываем коэффициенты для количества продавцов (x1)

a1, b1 = calculate_coefficients(y, x1)

print(f"Коэффициенты для количества продавцов (x1):")

print(f"Интерсепт (a): {a1}")

print(f"Коэффициент (b): {b1}")

# Рассчитываем предсказанные значения y' для количества продавцов y_pred_x1 = a1 + b1 * x1

print("\nПредсказанные значения товарооборота (y') для количества продавцов:")

print(y_pred_x1)

# Рассчитываем коэффициенты для интенсивности покупателей (x2)

a2, b2 = calculate_coefficients(y, x2)

print(f"\nКоэффициенты для интенсивности покупателей (x2):")

print(f"Интерсепт (a): {a2}")

print(f"Коэффициент (b): {b2}")

# Рассчитываем предсказанные значения y' для интенсивности покупателей y_pred_x2 = a2 + b2 * x2

print("\nПредсказанные значения товарооборота (y') для интенсивности покупателей:")

print(y_pred_x2)

Также благодаря библиотеке pandas возможен легкий вывод результата в виде графика. Представим код для вывода значений, полученных теоретически и экспериментально для двух рассматриваемых случаев.

# Построение графиков

# График для количества продавцов

plt.subplot(1, 2, 1)

plt.scatter(x1, y, color='blue', label='Фактические значения (y)', alpha=0.6)

# График для интенсивности покупателей

plt.subplot(1, 2, 2)

plt.scatter(x2, y, color='blue', label='Фактические значения (y)', alpha=0.6)

# Показать графики

plt.tight_layout()

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

При запуске кода с чтением исходных данных из файла excelполучен результат, приведенный на рисунке 1.

	товарооборот	количество продавцов	интенсивность потока покупателей
0	293	12	12
1	527	23	5
2	685	34	11
3	701	35	10
4	702	34	15
5	835	40	13
6	433	23	16
7	577	26	23
8	768	46	25
9	316	22	14
10	152	11	7
11	315	24	3
12	34	3	2
13	23	2	3
14	34	3	2
15	23	1	4
16	23	2	3
17	31	3	2
18	24	2	3

Рисунок 1. Результат вывода исходной таблицы.

Figure 1. The output result of the original table.

При запуске кода с подсчетом параметров для двух случаев, а также прогнозируемых значений получен результат, представленный на рисунке 2.

Коэффициенты для количества продавцов (xl):

Интерсепт (а): -14.87301876006859

Коэффициент (Ь): 19.591292937691627

Предсказанные значения товарооборота (у') для количества продавцов: [220.22249649 435.72671881 651.23094112 670.82223406 651.23094112 768.77869875 435.72671881 494.50059762 886.32645637 416.13542587 200.63120355 455.31801174 43.90086005 24.30956712 43.90086005

4.71827418 24.30956712 43.90086005 24.30956712]

Коэффициенты для интенсивности покупателей (х2):

Интерсепт (а): 54.68793964147943

Коэффициент (Ь): 31.542943045155436

Предсказанные значения товарооборота (у') для интенсивности покупателей [433.20325618 212.40265487 401.66031314 370.11737009 527.83208532 464.74619923 559.37502836 780.17562968 843.26151577 496.28914227 275.48854096 149.31676878 117.77382573 149.31676878 117.77382573 180.85971182 149.31676878 117.77382573 149.31676878]

Рисунок 2. Результат полученной информации на второй вопрос.

Figure 2. The result of the information received for the second question.

Построенные графики приведены на рисунке 3.

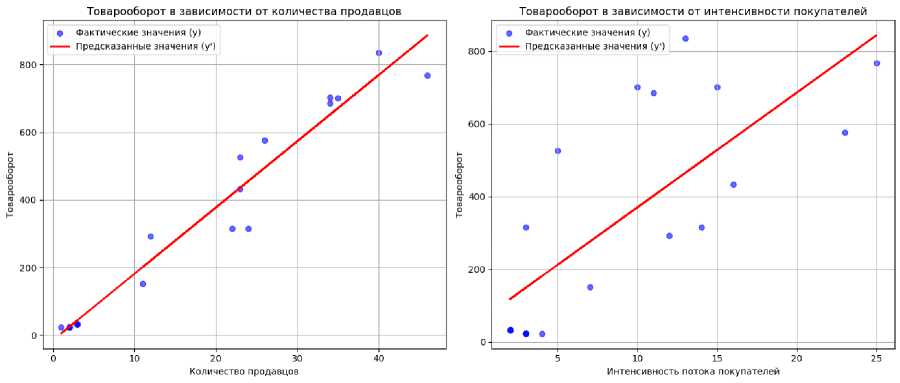
Рисунок 3. Графики фактических значений и предсказанных методом наименьших квадратов.

Figure 3. Graphs of actual values and those predicted by the least squares method.

Таким образом, получена функция, которая наиболее приближена к истинным значениям, полученным экспериментальным путем. В обоих случаях она представляет собой возрастающую функцию прямой. Полученная прямая называется линией линейной регрессии или линией наилучшего соответствия [6]. Можно сделать вывод, что метод наименьших квадратов позволяет определить наиболее приближенную к реальным значениям функцию кривой, по которой также возможно предсказать будущие значения. Этот метод позволяет построить точную модель для прогнозирования будущих результатов текущей задачи [7].

В итоге работы были построены возрастающие функции, представленные прямыми. Были выражены формулы для нахождения параметров метода наименьших квадратов, а также найдены по выведенным формулам параметры данных для различных точек одной марки магазина.

ЗАКЛЮЧЕНИЕ

Метод наименьших квадратов очень удобен для решения задач по построению прогноза. Благодаря простоте реализации и способа поиска параметров возможно получить коэффициенты функции, которая характеризует зависимость между рассматриваемыми переменными. Также метод наименьших квадратов обладает таким свойством как универсальность, что означает его применимость к различным задачам по построению кратковременного прогноза с использованием экспериментальных данных. Другое не менее важное свойство метода – эффективность, ведь с помощью метода наименьших квадратов можно получить предварительный прогноз и оценить исследуемую модель. Тем не менее, не смотря на все перечисленные преимущества метода, необходимо учитывать, что он используется только при линейных зависимостях между переменными. А также экспериментальные данные перед применением метода наименьших квадратов необходимо исследовать на существование неверных значений, которые сильно выделяются по сравнению с другими экспериментальными данными.

Статья