Применение метода оценок влияния нелинейностей на переходные процессы в нелинейных системах

Математический аппарат анализа нелинейных систем связан с необходимостью исследования нелинейных дифференциальных уравнений (ДУ), теория которых содержит множество индивидуальных методов, присущих различным видам уравнений, описывающих систему. Сложность решения нелинейных ДУ вызывает необходимость создания ряда приближенных методов, позволяющих судить о характере процессов, наблюдаемых в системе. При этом нелинейные характеристики реальных элементов системы заменяют приближенными линейными функциями.

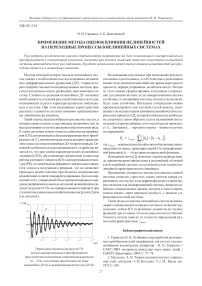
Такой подход нецелесообразен при анализе систем, в которых присутствуют существенные нелинейности и не всегда возможно получить решение в аналитическом виде. К таким системам можно отнести стабилизатор напряжения (СН), построенный на базе квазирезонансного преобразователя [1], математическая модель которого представлена в виде системы нелинейных ДУ второго порядка. Основной особенностью рассматриваемого устройства является то, что при замене параметрических нелинейных элементов (НЭ), обусловленных физической сущностью работы ключевого элемента (КЭ) в цепи резонансного контура (РК), на линейный коэффициент значительно снижается точность получаемого решения, что не позволяет проводить анализ системы при больших возмущающих воздействиях и синтез закона регулирования. Для подтверждения этих утверждений было промоделировано поведение напряжения на выходе исходной нелинейной модели исследуемого СН и ее линеаризованного варианта при ступенчатом уменьшении сопротивления нагрузки в 2 раза (см. рисунок).

Переходные процессы на выходе СН на базе квазирезонансного преобразователя при ступенчатом изменении сопротивления нагрузки 10.. .5 Ом, полученные при решении системы нелинейных ДУ (I) и линеаризованной системы ДУ (II)

На основании полученных при испытаниях результатов можно сделать вывод, что НЭ системы существенно влияет на ее динамические свойства: время переходного процесса, перерегулирование, колебательность. Исходя из этого можно сформулировать следующее утверждение для данной системы: если линеаризованная система устойчива, то нелинейная система, соответствующая ей, будет тоже устойчива. Последнее утверждение можно прокомментировать как частный случай вывода, основанного на методе оценок влияния нелинейностей на переходные процессы [2], который в общем виде необходимо дополнить таким образом: если в нелинейной системе имеются автоколебания, то их амплитуда не превышает 5 „ . Значение 5 „ - верхнюю оценку - можно получить по выражению ^

• ⁶ = z Л max '^[| h о| ⁺ | ^hi — h i - 1 1] ,

i = 1

где z _{Л max} -максимальное (по абсолютной величине) значение разности между характеристикой НЭ и линеаризованной функцией; h i - i- й экстремум переходной функции.

Описанный метод [2] позволяет оценить разницу между динамическими процессами в нелинейной и близкой к ней линейной системе, получаемой путем замены нелинейной характеристики на линейную.

Применение указанного метода для анализа данной системы позволит упростить задачу синтеза закона управления в том случае, если корректирующее устройство, рассчитанное для линеаризованной системы, является линейным динамическим звеном, которое в свою очередь можно связать через верхнюю оценку 8 „ с законом управления исходной системы.

Такой подход к анализу нелинейных систем не накладывает ограничений на порядок системы и позволяет исследовать любые НЭ: от релейных элементов до гладких функций, при условии, что исходная система устойчива. Точность метода зависит от точности определения разностной характеристики z _{Л max} .