Применение метода ортогональной циклической редукции для решения систем линейных алгебраических уравнений с матрицами специального вида

При решении различных прикладных задач [1] возникает необходимость в решении систем линейных алгебраических уравнений с блочной матрицей специального вида:

As = f, где A e^ n'(N 1)x( n' N+1) - постоянная блочная матрица, s = [ xT, xT,..., xT 0]T ейn'N+1, xz ейn, f e йn(N-1), 0 ей, векторы Xj, x , и параметр 0 - известны.

Уравнение (1) в матричном представлении имеет вид:

D i   K i

D ^   K 2

E i

E 2

x

x 2

f . f 2

D N - 2   K N - 2

D N - 1   K N - 1

^E N - 2

E N - 1

x N - 1

xN

^f N - 2

. ^fN - 1

где Di , Ki ей n ^x n , E_t ей n , l = 1, ... , N - 1.

Положим N = 2 k max + 1, где k^ задается исходя из вычислительных возможностей.

Уравнение (2) запишем в следующем виде:

Dlxl + Klxl+1 + Eft = fl, l = 1, ... , N-1.

Рассмотрим коэффициенты и свободные члены уравнения (3) при l — 1 и l , записав их в следующей форме:

(0    ЛГ<°)      О      7?(°)Г<°)

Dl—1   Kl—1     °     El—1

°    Di(°)  K<°)  EГ l   lll где D^ = Di , K = Kl , E = El , fi(0) = fi , l = 1, ... , N — 1.

Применим для решения системы (1) метод ортогональной циклической редукции.

Метод ортогональной циклической редукции состоит из прямого и обратного хода.

Прямой ход метода заключается в последовательном применении ортогональных преобразований к системе (4), так что на каждом этапе преобразований исключаются блоки с нечетными индексами l .

Ортогональная матрица преобразований имеет вид:

Г— D/k 1 K(■ 1 — K(■ 1 11 ,   ,     ,      ,   .     N — 1 Qlk—1) = _      — Dlk) Kl—k1) IJ ,    k = 1 ... , kmax , l = 2, ... , 2k —1 ,                           (5) где K = K 1.

Применяя ортогональное преобразование (5) к (4), получим:

Q ^{k —} 1)

_n ( k — 1)   _r( k — 1)      n       fk( k — 1)    X k — 1)

^D l — 1      K l — 1         °      E l — 1      f l — 1

°       Di ^{: k —} 1)    K ( ^{k —} 1)    Ei ^{: k —} 1)    fi ^{( k —} 1)

V ^{( k} )    — I   U ( ^k )    W ^{( k} )    r ^{( k}'

( k )                   ( k )         ( k )         ( k )

. ^Dl /2     ° K l /2    E l /2 fl /2

После последовательного применения преобразований k раз получим уравнение:

D_Y ⁽ k "a¹ ) X _o + K ( k  ' X_N + E ( k ^O = f ⁽ k m“\                                  (7)

Обратный ход заключается в вычислении неизвестных x по формулам:

X m = VX . — p + U l X m + , + Wk П + r , k = k „,.... 1, l = 2,..., N ^¹ ,                  (8)

где p = 2 k ^{— 1} , m = p • ( l — 1) + 1 .

Обозначим: ⁽ k ⁾-<П⁽ k ) Jk(k ) (k)k )   ⁽kk

^Y l   = { D l  , K l , E l , f l } ^k = °, ... , ^k max , l = 1, ... , N ¹ ,

(9) у ( k ⁾_)tE k ) tt( k ) w⁽k )    k )    t —t

Zl      { Vl   , Ul , Wl   , rl   } k 1, ... ,kmax, l   2, ... , N 1 , приведем схемы вычислений, производящихся на прямом и обратном ходе метода в случае, когда kmax = 3 .

k = 0

k = 1

k = 2

k = 3

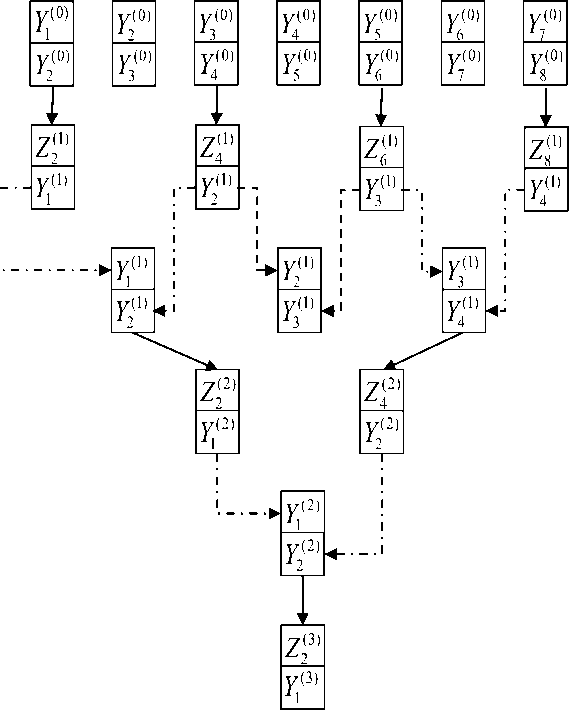
Рис. 1. Схема вычислений по прямому ходу метода.

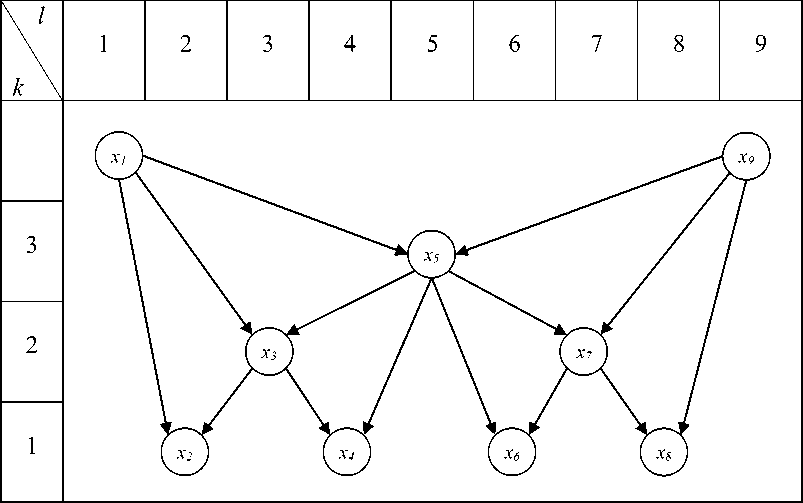
Рис. 2. Схема вычислений по обратному ходу метода.

Приведем примеры применения метода циклической ортогональной редукции для решения систем линейных алгебраических уравнений.

Пример 1. Рассмотрим систему вида (2), где k^ = 2, N = 5, n = 1. Зададим:

D i = 1, K = 2, E i = 1, f | = 4, l = 1,4 , x₁ = 1, x₅ = 1, 9 = 1.

Тогда система (2) примет вид:

	" 1_
"1  2  0  0  0  1 1 0  1  2  0  0  1	x 2 x 3	" 4 ’ 4
0  0   1   2  0  1 '	x 4	= 4
0  0  0  1   2  1 J	1 . 1 .	4

В результате применения метода ортогональной циклической редукции получим решение:

s = [ 11111 1 ] .

Пример 2. Рассмотрим систему вида (2), где k^ = 2 , N = 5, n = 2. Зададим:

Di =

, K i =

- 2  2

E l

i = 1,4 ,

-

	x 1 =					Г 1 1 .- 1 .	, x 5 =	Г 1 1 .- 1 .	, 9 = 3.
Тогда система (2) примет вид:
													Г11
	" 1	1	- 2	2	0	0	0	0	0	0	1 1		-1 1		■- 1"
	1	- 1	2	2	0	0	0	0	0	0	- 1		x x 2 1		- 1
	0	0	1	1	- 2	2	0	0	0	0	1				- 1
	0	0	1	- 1	2	2	0	0	0	0	- 1		X3, x з 1		- 1
	0	0	0	0	1	1	- 2	2	0	0	1	'		=	- 1
	0	0	0	0	1	- 1	2	2	0	0	- 1		x 4 X 4 1		- 1
	0 0	0 0	0 0	0 0	0 0	0 0	1 1	1 - 1	- 2 2	2 2	1 - 1				- 1 - 1
	1—										-1		- 1
													. 3 .

В результате применения метода ортогональной циклической редукции получим решение:

s = [ 1 - 11 - 11 - 11 - 11 - 1 3 f