Применение метода прямого моделирования Монте-Карло к задаче течения разряженных газов

Метод прямого моделирования Монте-Карло (ПММК) [1] применяется для симуляции течения разряженных газовых потоков. В данном методе используется прямое моделирование теплового движения молекул газа с помощью «тестовых» частиц. Для снижения потребного машинного времени в одной из разновидностей метода ПММК [2] помимо «тестовых» вводятся еще «целевые» частицы. Данные частицы участвуют в столкновениях с «тестовыми» частицами, что позволяет понизить порядок числа операций до N, где N – количество «тестовых» частиц. При этом каждой «тестовой» частице соответствует определенная «целевая» частица, которая с ней сталкивается. «Целевые» частицы вводятся в численную схему метода только на этапе моделирования столкновения частиц. После определения скорости «тестовых» частиц (после столкновения) «целевые» частицы в схеме метода не учитываются.

• 1.    ЧИСЛЕННАЯ СХЕМА МЕТОДА

В данной работе рассматриваются двумерные течения разряженных газов. Область течения разбивается однородной сеткой с квадратными ячейками. На каждом шаге по времени с границы течения, где выставляется скорость набегающего потока, в поток испускаются «тестовые» частицы. В каждую прилегающую к границе ячейку сетки помещается по одной частице. Координаты этих частиц внутри ячейки сетки определяются следующим образом:

y = R ' h ,

где ^R - случайная величина из диапазона R 'е [0,1)

,

• h – шаг сетки.

После того, как частицы были введены в поток, необходимо определить их скорости. Скорости определяются по формулам, приведенным ниже, которые были получены из условия равновесия границы. Компонента скорости перпендикулярная границе определяется как u = VZRTnTR'),          (2)

где R – универсальная газовая постоянная,

T. - температура набегающего потока, Q(U, R') — положительный корень уравнения: R‘ = exp[-(U - П)2 ] + УЛЦ[1 + erf (U - П)] (3) exp(-U2) + VkU(1 + erfU)     , где

U = u . /72rT : .           (4)

Здесь u. - x-компонента скорости набегаю- щего потока.

Тангенциальная к границе набегающего потока компонента скорости испускаемой тестовой частицы запишется как

12RT

M

M

Z R k - M | + v . ,   (5)

k=1        2 / где M – некоторое целое число, обычно [3] принимаемое 12,

• v . - y-компонента скорости набегающего потока.

На следующем этапе для каждой частицы вычисляется время необходимое ей, чтобы вылететь из ячейки (пересечь границу с соседней ячейкой).

^T b

r

u

Здесь (x, y) – координаты «тестовой» частицы до столкновения,

(x_c,y_c) – координаты «тестовой» частицы в момент столкновения.

Компоненты скорости «целевой» частицы

Здесь в числителе модуль вектора расстояния от точки нахождения «тестовой» частицы до точки пересечения с границей ячейки. В знаменателе

определятся как

^ui = ^u ,

– модуль вектора скорости частицы.

После этого для каждой «тестовой» частицы рассчитывается время ее свободного пробега между столкновениями по формуле:

= 1.225шУ2Й ;          (7)

^Tc 3p 4i?d4- lnR ' ) ’

12RT xi ( f ""M" lf= ?^{R k}

M

,

vi

12RT yi M

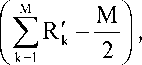
где p – давление, m – молекулярная масса воздуха, d2 – квадрат диаметра молекулы воздуха находится как d2 = 2J^..         (8)

3 ц 7^ 3

где (T_xi, T_yi) – компоненты кинетической температуры i-ой «тестовой» частицы.

Компоненты «тестовой» частицы после соударения с «целевой» частицей находятся как u' = u + wy sin 8 cos v sin V - wx cos2 V,

Здесь k - постоянная Больцмана, ц - динамическая вязкость.

Если T b < T _c , считается, что «тестовая» частица покинула ячейку и перешла в соседнюю.

Если T b > т _с , считается, что произошло столкновение между «тестовой» и «целевой» частицами.

«Тестовые» частицы могут также сталкиваться с твердыми границами. В этом случае возможны два варианта: зеркальное, либо диффузное отражение. При зеркальном отражении тангенциальная к стенке компонента скорости не изменяется, а нормальная компонента меняет знак. При диффузном отражении скорости частицы определяются по формулам:

u = u b + 7 2RT_b( - lnR ' ) ,        (9)

v' = v + wx sin 8 cos v sin V - wy cos2 V ,(13) где (u, v) – компоненты скорости «тестовой» частицы, wx = u - ui

W y = V - V i ,              (14)

параметры столкновения 8 и V статически определяются [4] как

8 = 2 n R ' ,                (15)

V =

Г

1 +

V

(V 0max R ' ) 4 J

где ^V0max = ^1,5 , to ( n ) - эллиптический интеграл первого

рода,

Г ^к/

^{ю ( п )} = 1

d ф

71 -П ² sin² Ф

v = v b

12RTb M

M

I Z ^Rk

V k = 1

M

где ^ub v b 0 - компоненты скорости неподвижной стенки,

T b – температура стенки, u – нормальная к стенке компонента скорости, v – тангенциальная к стенке компонента скорости.

После определения этих компонент скорости алгоритм метода возвращается к определению времени T _b .

Если T b > т _с произошло столкновение между частицами, то «тестовая» частица перемещается в точку столкновения:

x_c = x + U T c ,

У с = У ⁺ v ^T c .              (11)

После этапа столкновений частиц следует этап вычисления параметров потока. Скорость

потока в каждой ячейке определяется следующим

образом

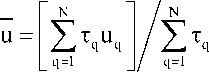
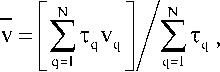
где (u_q,v_q) – компоненты скорости q-ой тестовой частицы,

T q - время, проведенное q-ой тестовой частицей в рассматриваемой ячейке.

Кинетическая температура рассчитывается как

T = -u- xnR

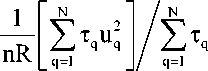
T y =

v2

nR

^T q ,

где n – количество частиц, которое находилось в данной ячейке в рассматриваемый момент времени.

На этом численная схема метода завершается. После этого новые «тестовые» частицы вводятся в поток во входном сечении.

Блок-схема метода представлена на рис. 1. Здесь nt – число шагов по времени.

2. НЕКОТОРЫЕ ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Рассмотрим течение за плоской пластиной, поставленной поперек разряженного потока. Область течения представляет собой прямоугольник 100 на 20 см разделенный на 100 х 20 ячеек сетки. Ширина пластины 10 см . Сечение, в котором измерялась компонента скорости u, находилось в 10 см за пластиной (см. рисунок 2). Давление равнялось 101,325 Па . Скорость набегающего потока u „ = 10 м/с . Температура пластины и потока 273 К . В процессе расчета было выполнено 50000 шагов по времени.

Было также рассмотрено моделирование свободной струи. Расчетная область представляла собой прямоугольник размерами 100 на 10 см , в верхней половине которого распространялась свободная струя с u „ = 10 м/с , в нижней половине прямоугольника газ был неподвижен. Сетка пред-

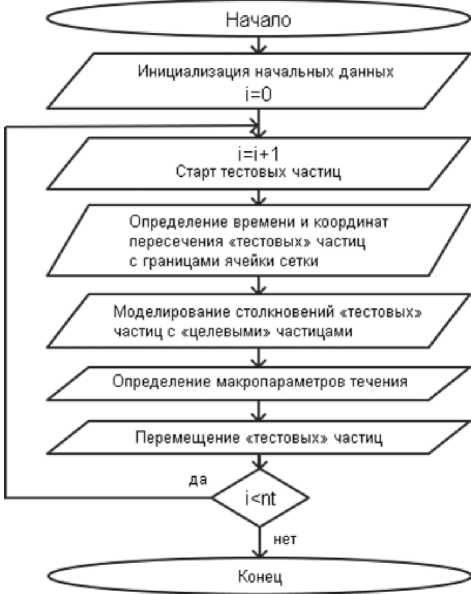
Рис. 1. Блок-схема метода ПММК

ставляла собой 100 х 10 ячеек. Температура струи и неподвижного газа равнялась 273 K . Давление равнялось 101,325 Па . В процессе расчета было выполнено 100000 шагов по времени. Результат представлен на рис. 3. Сечение, в котором измерялась компонента скорости u , находилось в 9 см от входной границы расчетной области.

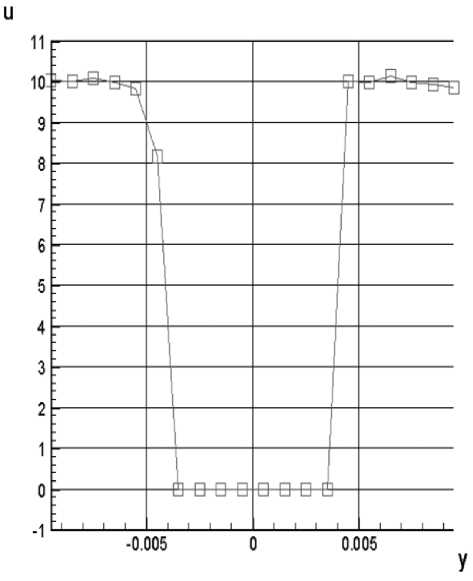
Рис. 2. Профиль продольной компоненты скорости u за плоской пластиной

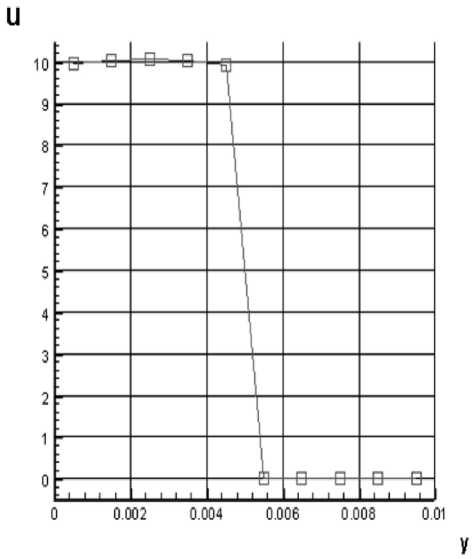
Рис. 3. Профиль продольной компоненты скорости u в зоне контакта струи с неподвижным газом

ВЫВОДЫ

По численным результатам моделирования методом ПММК можно сделать следующий вывод, что близлежащие слои течения слабо влияют друг на друга. При моделировании обтекания плоской пластины, граничный к пластине слой увлекает с собой только соседний неподвижный слой за пластиной. При моделировании течения свободной струи, увлечения соседнего неподвижного слоя не происходит.