Применение метода пропорциональной навигации при решении задач судовождения

Соловьев А. А. и др. Применение метода пропорциональной навигации при решении задач судовождения. Вестник МГТУ. 2022. Т. 25, № 4. С. 400–408. DOI:

Разработка методов и алгоритмов управления судном при маневрировании относительно подвижного объекта является актуальной задачей судовождения. Методы сближения одного объекта (преследователя) с другим подвижным объектом (целью) по характеру связи между углом скорости преследователя и углом визирования на цель делятся на две группы:

– методы с фиксированным направлением вектора скорости относительно линии визирования (метод кривой погони, метод постоянного угла упреждения);

– методы с переменным направлением вектора скорости относительно линии визирования (метод параллельного сближения, метод пропорциональной навигации).

Эти методы сближения широко применяются при решении задач перехвата летательных аппаратов ( Zarchan, 1995; Проектирование…, 2001; Маркевич и др., 2018 ) и в значительно меньшей степени – при выполнении задач судовождения. Применительно к задаче сближения судна с подвижным объектом обычно используется математический анализ движения двух точек ( Фадюшин, 2012; 2013 ), в ходе которого не учитываются динамические характеристики судна и возможности применения какого-либо метода сближения при данных начальных условиях.

Рассмотрение динамики идеального движения позволяет учесть указанные факторы. Под идеальным движением понимают движение твердого тела, центр инерции которого движется точно по траектории пропорциональной навигации ( Кельзон, 1959; Кан и др., 1965; Platus, 1982 ). Изучение динамики идеального движения производится при следующих ограничениях: 1) движение цели равномерное и прямолинейное; 2) скорость судна постоянна. В отличие от кинематического исследования, судно рассматривается как твердое тело, управляемое рулевым устройством и движущееся под действием силы тяги винта, гидродинамических и инерционных сил и их моментов.

Динамический анализ идеального движения позволяет судить о возможности осуществления маневра при данных начальных условиях, а также построить не только траектории движения судна, но и графики изменения угла перекладки руля, угловой скорости и угла дрейфа в процессе всего маневра.

Теоретические основы

Для вывода уравнений, учитывающих динамические характеристики судна при его маневрировании относительно подвижного объекта, рассмотрим кинематические уравнения движения двух точек (рис. 1).

На рис. 1 указаны следующие обозначения: точка В – цель, которая движется по курсу К В со скоростью V B ; точка С – судно, движущееся со скоростью V C (угол скорости q ); D – дистанция между точками; Θ – угол визирования. Обозначение и направление осей координат соответствуют принятым в теории управляемости корабля¹ ( Соболев, 1976; Титов и др., 2019 ).

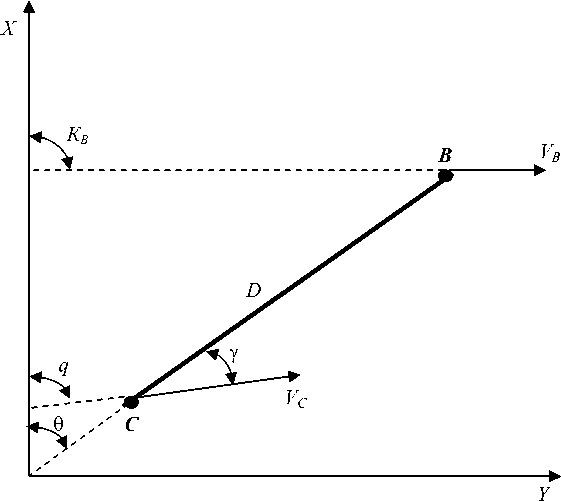
Рис. 1. Кинематические параметры движения судна и цели Fig. 1. Kinematic parameters of vessel and target movement

Учитывая параметры движения точек В и С , находим скорости изменения угла визирования и дистанции между ними:

₌ V B sin K B - ^{0 ) -} V c sin ( q - ⁰ )

D = V_B cos ( K_B - 0) - V_c cos ( q - 0 ) .

В теории пропорциональной навигации скорость изменения угла курса судна q должна быть пропорциональна скорости изменения угла визирования 0 :

q = K0,(3)

где К – коэффициент пропорциональности (навигационная постоянная).

Интегрируя уравнение (3), получим q = K0 + C,(4)

где С – постоянная интегрирования, зависящая от начальных условий, например, в момент времени t = 0:

C = q - K0O,(5)

здесь q 0 и 0 0 - начальные значения угла скорости судна и угла визирования.

Введем понятие угла упреждения y = q - 0, тогда с учетом уравнения (4) постоянная интегрирования имеет вид

С = 0 (1 - К) + Y.(7)

Если К = 1 и у = 0, то сближение будет осуществляться по кривой погони, т. е. в любой момент времени q = 0 . В случае К = 1 и С ф 0 преследование цели происходит с постоянным углом упреждения C = q - 0 = у . Если К = 1 и q = 0 = 0, то выполняется параллельное сближение. Если K ф 1, то сближение осуществляется методом пропорциональной навигации. Выбор метода сближения зависит от ее конечной цели и маневренных характеристик судна.

Подставляя уравнение (4) в выражения (1) и (2), получим уравнения для расчета производных Θ и D для любого способа сближения:

.   {V_B sin( K_B - 0) - V _c sin [ 0( K - 1) + C ] }

0 = _L_B------B--------C----1Л

D

D = V cos(KB - 0) - Vc cos[0(K -1) + C].

Общую модель произвольного движения судна в горизонтальной плоскости представим следующей системой дифференциальных уравнений² ( Юдин и др., 2012 ):

m (1 + kxx)3 cos в - m (1 + ki)» в sin в + m (1 + k^ 2)» ю sin в = Te - Xk - Xp,(10)

• - m (1 + k2)3 sin в - m (1 + k^ 2)d в cos в + m (1 + k J» ю cos в = Y^ + YB - YP + YA,(11)

Jz (1+ k66)Ю- m (k22 - k 1)32sin в cos в = M^ + Mp - Mb - Ma,(12)

где k 11 , k 22 – коэффициенты присоединенных масс вдоль продольной и поперечной осей судна; k 66 – коэффициент присоединенного момента инерции; m – масса судна; J_Z – момент инерции судна относительно вертикальной оси OZ ; X _р, Y _р, M _Р – продольная, поперечная силы на руле и момент, создаваемый поперечной силой руля относительно ЦТ судна; X _K, Y _K, M _K – продольная, поперечная корпусные силы и момент, создаваемый поперечной корпусной силой относительно ЦТ судна; Y _В, M _В – поперечная сила от гребного винта и момент, создаваемый этой силой относительно ЦТ судна; Y _А, M _А – поперечная аэродинамическая сила и момент, создаваемый данной силой относительно ЦТ судна; T _Е – полезная тяга гребного винта; в - угол дрейфа судна; to - угловая скорость судна.

Для получения автономного уравнения, связывающего угол скорости судна q с углом перекладки руля a R , используем линеаризованные уравнения движения, которые описывают движение судна в процессе слабого маневрирования:

to = Bx в + B2 to + B3 aR,(13)

в = A в + A to + A aR,(14)

q = to - в.(15)

где в - угол дрейфа судна; to - угловая скорость судна; a R - угол перекладки руля; q - угол скорости судна; А ₁ – А ₃ и В ₁ – В ₃ постоянные коэффициенты.

Постоянные коэффициенты А ₁ – А ₃ и В ₁ – В ₃ зависят от конструктивных параметров судна:

( K y a₃ L C + E T X P 1 P ) ( р F D /2 ) - m ( 1 + k 11 ) m ( 1 + k _{2 2})

= - ⁽ E ^X P + Ka , )           E р F^

2 m (1 + k ₂₂) ^P D C ’     ³    2 m (1 + k ₂₂),

( K' m b 2 L c + E ^X P ) р F D V C

Ba =--7--------7----------,

• ¹             2 Jz ( 1 + k 66 )

_ ( b L C - E^ X p ) р F D V C     E_E_TV р F D V C

,     BA                       .

• 2    m ( 1 + k 66 )             ³   2 Jz ( 1 + k 66 )

где m – масса судна; k 11, k 22 – коэффициенты присоединенных масс жидкости; F D – площадь подводной части диаметральной плоскости; p - массовая плотность воды; L C - расчетная длина судна; J Z - момент инерции массы судна относительно вертикальной оси; k ₆₆ – коэффициент присоединенного момента инерции; E T - гидродинамическая эффективность руля; X P - приведенный коэффициент спрямляющих воздействий корпуса и струи гребного винта; l P – расстояние между ЦТ судна и баллером руля; a 1 – a 3 и b 1 – b 3 – коэффициенты поперечной силы и момента рыскания; K ‘ , K , K ‘ - поправочные коэффициенты, учитывающие влияние скуловых килей.

Система уравнений (13)-(15) содержит три неизвестных (в, to, q), каждое из которых принципиально может быть принято за управляемую координату, и один параметр управления aR. Последовательным исключением из системы уравнений неизвестных параметров, кроме одного, можно получить независимые уравнения относительно каждой управляемой координаты. Автономное уравнение, связывающее угол скорости с углом перекладки руля, имеет вид q + C1 q + C2 q = C3a R + C4 a R, (16)

где С ₁ = В ₁ + А ₂; С ₂ = А ₂ В ₁ – А ₁ В ₂; С ₃ = В ₂ А ₃ – А ₂ В ₃; С ₄ = В ₃ – А ₁ В ₃ + В ₁ А ₃ .

Уравнение (16) содержит вторую и третью производные от угла скорости судна q, которые выражены через угол визирования 0 и с учетом выражения (3) имеют вид q = K0,  q = K0.(17)

Для решения уравнения (16), как это видно из уравнения (17), необходимо дважды продифференцировать выражения (8) и (9):

0 = - {V cos(KB -0) + Vc (K-1)cos[0(K-1) + C] +D}0/D,(18)

0 = - { { V _s [ 0cos ( K_B - 0 ) + 0 ² sin ( K - 0 ) ] + V_c ( K - 1 ) {0 cos [0 ( K - 1 ) + C ] -

- 02 (K -1)sin[0(K -1) + C] } + D0 + 2D0 }} / D,

D = {V sin(KB-0) + Vc sin[0(K-1) + C](K -1) } 0.

С учетом уравнений (3) и (15) автономное уравнение (14) имеет следующий вид:

К 0 + КС. 0 + КС 0 = C a„ + C a„.

1           2        3 R 4 R

Таким образом, задавая начальные значения VC, q, VB, KB, D и 0, а также способ сближения (коэффициент пропорциональности К и начальный угол упреждения у), из уравнения (21) получим закон изменения угла перекладки руля aR и построим траекторию движения судна, рассчитав его координаты по формулам:

X_c = Vc cos q ,                                         (22)

Y_c = V sim q.                                        (23)

Подставляя a R в систему уравнений (13)-(15), определим изменение угла дрейфа в и угловой скорости судна го , используя которые, вычислим все гидродинамические силы и моменты, действующие на корпус судна.

Следует отметить, что если при сближении методом пропорциональной навигации угол упреждения у может быть любым, то при параллельном сближении он должен удовлетворять требованию

V sin y = — sin (KB - ®).                                    (24)

V C

Данное требование следует из уравнения (1), в котором с учетом выражения (6) примем 0 = 0 .

Сближение судна с подвижным объектом является важной, но не единственной задачей судовождения, при решении которой применим метод пропорциональной навигации. Представляет интерес реализация всестороннего обхода подвижного объекта (например, с целью его изучения). Такой маневр может быть осуществлен способом удерживания цели на постоянном курсовом угле или постоянной дистанции от нее.

При маневрировании на постоянном курсовом угле К_у угол упреждения вычисляется следующим образом:

Y = в + К,, где в - угол дрейфа судна.

При маневрировании на постоянной дистанции от цели система уравнений (8), (9), (18)–(20) упрощается: уравнения (9) и (20) исключаются, а уравнения (18) и (19) будут иметь вид

0 = - V cos(KB-0) + Vc (K-1)cos[©(K-1) + C^0/D,(26)

0 = - { { V_B [© cos ( K_B - 0 ) + 0 2 sin ( K_B - 0 ) ] + V . ( K - 1 ) { © cos [© ( K - 1 ) + C _J -

-02 (K-1)sin[©(K -1) + CJ }}} /D.(27)

Угол упреждения должен удовлетворять требованию cos y = VB- cos (KB - 0),(28)

VC которое следует из уравнения (2), если принять D = 0.

Результаты и обсуждение

Математическая модель (7)–(9), (13)–(15), (18)–(23) позволяет просчитать варианты сближения судна с подвижным объектом при использовании всех рассмотренных выше способов и начальных условий сближения: позиций цели относительно судна; отношений скоростей движения судна и цели; разности курсов судна и цели; начального угла упреждения.

На рис. 2 и 3 показаны расчетные траектории движения судна при наведении на подвижный объект. Начальные условия в обоих случаях одинаковы: курс судна – 0°, скорость судна – 10 узл, пеленг на цель – 0°, дистанция – 1 200 м, курс цели – 90°, скорость цели – 5 узл. Маневр сближения выполнялся методом пропорциональной навигации при коэффициентах пропорциональности К = 1 и К = 4.

Анализ динамики судна в процессе наведения с использованием различных коэффициентов пропорциональности может производиться на основании сравнения законов изменения перекладки руля и угловой скорости судна. При расчете результатов маневра до начала его реального выполнения судоводитель имеет возможность спрогнозировать развитие навигационной ситуации и заблаговременно принять решение по безопасному управлению судном.

Сравнительный анализ траекторий сближения позволяет отдать предпочтение сближению при К = 4, однако окончательный вывод можно сделать только после сравнительного анализа кинематических и динамических параметров движения судна.

Графики изменения угла перекладки руля при различных коэффициентах пропорциональности в зависимости от дистанции сближения с целью (рис. 4) свидетельствуют о том, что при всех значениях K > 1 максимальные углы перекладки руля соответствуют начальному периоду сближения и убывают до нуля тем быстрее, чем больше коэффициент пропорциональности К. Это связано с тем, что угловая скорость имеет наибольшее значение в начальный период сближения и к концу маневра стремится к нулю. При К = 1 угловая скорость, наоборот, неограниченно возрастает в конце маневра (когда судно находится в непосредственной близости от цели), что делает этот способ сближения практически непригодным при выполнении задач судовождения.

Рис. 2. Траектории сближения при К = 1

Fig. 2. Approach trajectories at K = 1

Рис. 3. Траектории сближения при К = 4

Fig. 3. Approach trajectories at K = 4

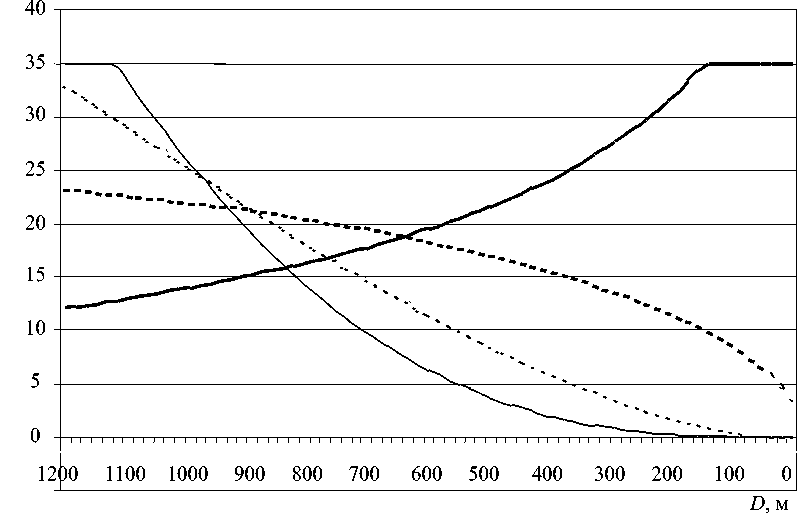
К = 1■ ■ ■ ■ К = 2       К = 3       К = 4

Рис. 4. Зависимость угла перекладки руля от дистанции до цели при различных коэффициентах пропорциональности

Fig. 4. Rudder angle dependence on the distance to the target with different proportionality coefficients

Таким образом, выбор коэффициента пропорциональности представляет собой отдельную задачу, которую необходимо решать с учетом конкретных начальных условий и конечной цели сближения.

Траектории движения судна относительно подвижной цели на постоянном курсовом угле и постоянной дистанции показаны на рис. 5 и 6. Начальные условия для обоих вариантов одинаковы: скорость судна V C = 10 узл, скорость цели V B = 2 узл, курс цели К В = 0°, пеленг на цель θ = 80°, дистанция до цели

D = 250 м. При выполнении первого маневра цель удерживается на постоянном курсовом угле К_у = 90°, второго маневра – на постоянной дистанции D = 250 м.

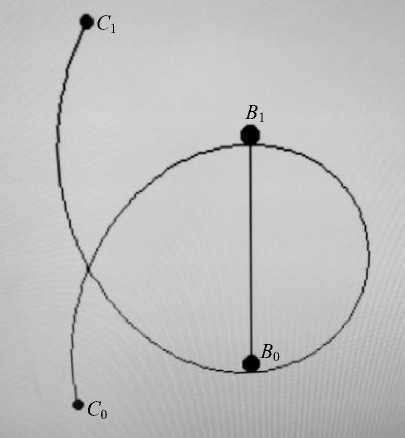
Рис. 5. Траектория судна при маневрировании на постоянном курсовом угле

Fig. 5. Vessel's trajectory when maneuvering at a constant heading angle

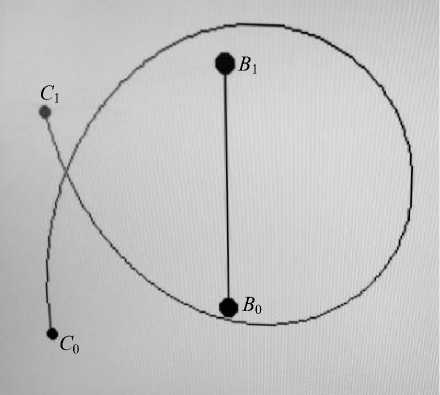
Рис. 6. Траектория судна при маневрировании на постоянной дистанции

Fig. 6. Vessel's trajectory when maneuvering at a constant distance

При маневрировании на постоянном К_y дистанция до цели плавно уменьшается до 170 м в середине маневра, а затем опять увеличивается до начального значения (250 м). При маневрировании на постоянной дистанции курсовой угол плавно убывает с 90° до 75°, а затем увеличивается до начального.

Графики изменения угла перекладки руля α _R , угла дрейфа β и угловой скорости ω в процессе маневрирования представлены на рис. 7 и 8.

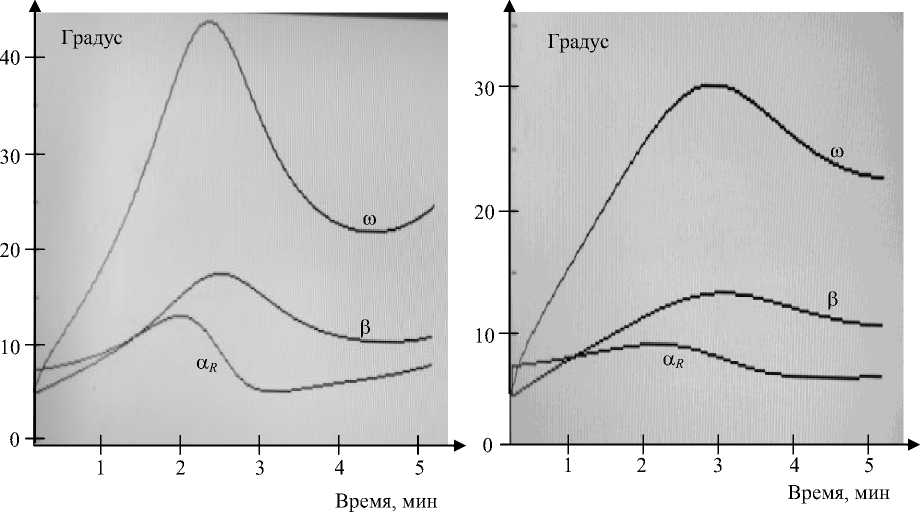
Рис. 8. Графики зависимости угла перекладки руля α _R , угла дрейфа β и угловой скорости ω при маневрировании на постоянной дистанции Fig. 8. Graphs of the dependence of rudder rudder angle α R , drift angle β and angular velocity ω when maneuvering at a constant distance

Рис. 7. Графики зависимости угла перекладки руля α _R , угла дрейфа β и угловой скорости ω при маневрировании на постоянном курсовом угле Fig. 7. Graphs of the dependence of rudder angle ω R , drift angle β and angular velocity ω when maneuvering at a constant heading

Анализ этих графиков позволяет отдать предпочтение второму способу маневрирования – на постоянной дистанции до цели, так как в этом случае значения угла перекладки руля, угла дрейфа и угловой скорости имеют гораздо меньшие значения при данных начальных условиях.

Рассмотренные в настоящей работе вопросы не исчерпывают весь спектр задач применения метода пропорциональной навигации в судовождении; например, представляет интерес решение следующих проблем: 1) сближение (уклонение) буксируемого судном объекта с другим подвижным объектом; 2) выбор маневра удаления от цели.

Заключение

В результате исследования получено автономное уравнение движения судна, управляемого по углу скорости, с помощью которого определена возможность применения известных способов сближения судна с подвижным объектом (кривая погони, кривая постоянного угла упреждения, параллельное сближение, метод пропорциональной навигации).

В процессе изучения установлено, что наиболее общим является метод пропорциональной навигации, с помощью которого разработана математическая модель движения судна при маневрировании относительно подвижного объекта.

Математическая модель предусматривает предварительный расчет экстраполируемых координат судна. Построение траекторий движения судна при любом заданном коэффициенте пропорциональности производится с учетом динамики судна и позволяет получить закон перекладки руля, а также спрогнозировать изменение в процессе маневрирования таких параметров судна, как угловая скорость и угол дрейфа.

Предложенная математическая модель может быть использована для алгоритмического и программного обеспечения автоматизированных систем управления судном при маневрировании относительно подвижного объекта.