Применение метода рассеянного поля для FDTD-моделирования электромагнитных полей вблизи диэлектрических и металлических наночастиц

Для моделирования проблем рассеяния электромагнитных плоских волн пространственно ограниченными объектами различных размеров широко используется метод FDTD (Finite-Difference TimeDomain [1, 2]). В рамках этого метода возбуждение плоских волн обычно реализуется по методам TF-SF (Total Field – Scattered Field) или SF (Scattered Field), см., например, [2 – 9] и ссылки в этих работах. При этом моделируются несколько типов электромагнитных полей: падающее – поле в отсутствие объектов, рассеивающих излучение (далее такие объекты для краткости будем называть «рассеивателями»); рассеянное – поле, возникающее в результате взаимодействия рассеивателей с падающим полем; полное поле – векторная сумма падающего и рассеянного поля. В случае метода TF-SF расчётная область разбивается на подобласти полного и рассеянного поля, разделённые границей, генерирующей падающее поле и «проводящей» его через область полного поля. При использовании метода SF уравнения Максвелла преобразуются таким образом, что требуется расчёт FDTD-методом только рассеянных полей (в предположении, что падающее поле изначально известно).

Метод ТF-SF в классической формулировке имеет ряд ограничений в случае, если геометрия задачи предполагает наличие бесконечных в одном из направлений тел (например – плоская граница раздела двух сред) или пространственная форма возбуждения отличается от волны с плоским фронтом. Следует также отметить, что для полноценной реализации TFSF-метода или его модификации необходимо внести изменения непосредственно в исполняемый код программы, реализующий алгоритм FDTD, с последующей её отладкой и компиляцией.

Реализацию метода SF можно осуществить на уровне языка задания параметров, имеющегося в настоящее время у большинства из распространённых программных пакетов, использующих алгоритм FDTD, то есть усилиями непосредственно пользователя программного комплекса. Такой подход реали- зован в настоящей работе при использовании распространённого пакета Meep [10], где в качестве входного языка подготовки заданий для выполнения FDTD-ядром использован язык функционального программирования Scheme.

Одним из ключевых аспектов применения любого численного метода является верификация его результатов и определение условий использования метода для решения конкретных прикладных задач. В настоящей работе FDTD SF-моделирование использовано в качестве основного метода исследования интенсивностей электромагнитного поля вблизи сферических диэлектрических и металлических наночастиц (НЧ) при условиях, близких к условиям реализации локализованных поверхностных плазмонных резонансов [11, 12]. Для простейших модельных систем (НЧ в воздухе, НЧ вблизи границы раздела двух диэлектриков) выполнено сравнение результатов, полученных по SF- и TF-SF-методам, с точным аналитическим решением согласно теории Ми [11, 12].

Как отдельный случай исследованы нанокомпозиты на основе металлических НЧ и высококремнезёмных стёкол, полученные при использовании золь-гель технологий [13–15]. Наноструктурированные стёкла, допированные НЧ восстановленных металлов, используются в качестве материалов, применяемых для управления параметрами лазерного излучения, оптической записи информации, создания сенсорных элементов [13]. Свойства этих материалов сильно зависят от формы, концентрации, взаимного расположения НЧ, свойств диэлектрической матрицы. В частности, установлено, что для золь-гель стёкол, содержащих НЧ восстановленных металлов, возможно создание условий, при которых наведённое локальное изменение показателя преломления остаётся стабильным в течение длительного времени [13–15], что представляет интерес для приложений оптики и на-ноплазмоники. Средний размер металлических НЧ (Ag, Cu, Ni, Co, Mn) в золь-гель стекле лежит в диапазоне от единиц до сотен нанометров. Экспериментальная реализация эмпирически подобранной струк- туры для получения материала с заданными свойствами на основе таких нанокомпозитов является дорогостоящей и длительной. Компьютерное моделирование распределения электромагнитных полей (особенно в области ближнего поля) существенно сокращает время перебора оптимальных вариантов нано- и микроструктур и позволяет предложить новые материалы, формирующие заданный оптический отклик [16].

Таким образом, основными целями работы являются: во-первых, верификация и сравнение результатов FDTD-(по методикам SF, TF-SF) моделирования диэлектрических и металлических НЧ; во-вторых, исследование с помощью разработанных моделей характеристик локального оптического отклика (ближнего поля) базовых наноструктур для указанного класса композитных материалов, важных для оптических приложений.

Остальная часть статьи организована следующим образом. Основы метода SF приведены в разделе 1. Результаты численных экспериментов, графического анализа, а также сравнение данных (пространственных распределений интенсивности и характеристик усиления ближнего поля), полученных при FDTD-(SF, TF-SF) моделировании и использовании точного решения Ми для отдельной сферической диэлектрической или металлической (серебряной) НЧ, рассмотрены в разделе 2. Аналогичные данные, но при наличии плоской границы раздела двух диэлектриков (воздуха и золь-гель стекла) вблизи НЧ рассмотрены в разделе 3. В разделе 4 предложена простая аналитическая оценка влияния плоской границы раздела на ближнее поле НЧ (на основе результатов FDTD-моделирования), которая согласуется с результатами раздела 3. В заключении сделаны выводы по полученным результатам с учётом их возможного использования при создании новых оптических материалов на основе золь-гель стёкол и НЧ.

E ( r , to ) = E inc ( r , to ) + E sca ( r , to ),                     (3)

H ( r , to ) = H inc ( r , to ) + H sca ( r , to ),                  (4)

где E _inc ( r , to ) и H _inc ( r , to ) - поля при отсутствии рассеивателей в моделируемой задаче (эти поля полагаются известными), E _sca ( r , to ) и H _sca ( r , to ) - поля, возникающие в результате взаимодействия падающих полей с рассеивателями (эти поля должны быть определены в результате моделирования).

Из уравнений (1-4) можно получить следующие соотношения:

Vx Einc (r, to) = 'to Hinc (r, to), c

V х Hinc (r, to) = - — еinc (r, to)Einc (r, to) , c

^{Vx E} sca ^{( r} , ^{to )} = ~ ^H sca ^{( r} , ^{to )} , c

V X Hsca (r, to) = -— e(r, to)Esca (r, to) + Str to) , c

S(r, to) = - — ieir. to) - en (r, to))Einc if, to) .

c

Мы предполагаем, что решения уравнений (5, 6) и вид зависимости е _inc ( r , to ) от частоты и координат известны. Выполняя операцию обратного преобразования Фурье F ^-1 над каждым членом уравнений (7-9), получим набор уравнений Максвелла во временной области, которые требуется решить:

^{Vx E} sca ^{( r} , t ) = ^{1 d} t ^H sca ^{( r} , t ), c

^{Vx H} sca ( r , t ) =

= F -¹ J - —e ( r , to ) E sca ( r , to ) | + S ( r , t ), ’ I c                            J

1.    Постановка задачи и основы реализации SF-метода

Рассмотрим постановку задачи моделирования при использовании SF-метода [5, 7-9]. Уравнения Максвелла в частотной области для линейной, изотропной и немагнитной среды можно записать в виде:

Vx E ( r , to ) = — H ( r , to ), c

S ( r , t ) = F -^{1 J} - - (e ( r , to ) - e inc ( r , to )) E inc ( r , to ) [ .   (12)

I c                                                        J

В случае отсутствия у каждой из частей среды свойства частотной дисперсии первый член из правой части уравнения (11) и выражение (12), содержащие оператор F ¹, примут вид:

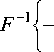
~ ^{e ( r} , ® ^{) E} sca i f , toH = ^{- 1 e ( r ) d} t ^E sca ^{( r} , t ), c                      J c

S(r, t) = -1 (e(r) - einc (r))d tEinc (r, t) . c

В общем случае использование формул (10), (11) при реализации метода FDTD в средах с частотной дисперсией требует задания аналитического выражения для зависимости диэлектрической проницаемости от частоты [2, 5]. В результате возможно использование метода SF и при учёте частотной дисперсии среды. Для расчёта вектора S (r, t) также необходимо знать явный вид Einc (r, ω). Возможна реализация метода SF при возбуждении: монохроматической волной; импульсом конечной длительности, определяемым зависимостью Einc (r, ω). Для получения стационарного распределения поля на заданной частоте в первом случае достаточно установить время моделирования, существенно превышающее период возбуждающей волны, а во втором – сохранять результаты расчётов пространственного распределения полей в промежуточных временных точках и выполнить впоследствии соответствующее преобразование Фурье [2, 5]. Далее будем рассматривать случай стационарного монохроматического возбуждающего поля с частотой ω0 : Einc(r, t) = Ei0nc(r) exp(-iω0t) . В этом случае выражение (12) принимает явный вид: S(r,t) = - iω0 (ε(r,ω0) - εinc(r))Ei0nc(r)exp(-iω0t). (13) c

Для расчёта распределения поля вблизи металлической НЧ выражение для частотной зависимости ε ( r , ω 0 ) выбиралось в характерной для металлов форме Друде, параметры этой зависимости выражались через действительную и мнимую части диэлектрической проницаемости на частоте возбуждения в виде, предложенном в [17]. Путём непосредственного численного эксперимента нами установлено, что при таком выборе дисперсионной зависимости диэлектрической проницаемости итерационное решение уравнений (10)–(12), выполняемое методом FDTD, сходилось к некоторому стационарному решению.

Согласно формулам (7)–(9), уравнения Максвелла преобразованы таким образом, что FDTD-методом требуется определить только рассеянные поля (с учётом того, что изначально известны падающие поля). Диэлектрические проницаемости ε inc и ε соответствуют геометриям моделируемой системы при отсутствии и наличии рассеивателей. Вектор-«источник» S (единственная величина в уравнениях (7), (8), зависящая от падающего поля) ненулевой только в областях модельного пространства, где значения ε inc и ε отличаются. В частности, если рассеиватель размещён в областях с различными значениями ε inc (например, включает границу раздела двух сред для начальной постановки задачи), то такому рассеивателю соответствуют несколько источников (векторов S ) в (8). Много источников также появляется при наличии многих дискретных рассеивателей в однородных областях модельного пространства.

Если поля E inc , H inc , соответствующие начальной постановке задачи, характеризуются фазовым множителем плоской монохроматической волны exp [ i ( kr ) – i ω t ], где k – волновой вектор (комплексный в поглощающих средах), то определение этих полей существенно упрощается для многих важных для приложений задач. В частности, для задач о рассеивании излучения объектами (например, НЧ), размещёнными вблизи плоской границы раздела двух однородных сред с локальными материальными параметрами, падающее поле имеет вид:

E _inc ( ω , r )

E i ⁰ nc ( ω , r ) + R E i ⁰ nc ( ω , r ), T E i ⁰ nc ( ω , r ),

где верхнее выражение соответствует области падающей на границу волны (первая среда), E _i ⁰ _nc ( ω , r ) , и волны, отражённой от границы, R E _i ⁰ _nc ( ω , r ) , а нижнее выражение – области прошедшей через границу волны (вторая среда); R и T – известные матрицы, характеризующие коэффициенты отражения и пропускания. Метод SF также достаточно просто обобщается на случай многослойных сред, включающих различные виды дискретных рассеивателей [7, 8].

Таким образом, при применении метода SF моделируемая задача может упрощаться за счёт использования известных точных аналитических решений граничных задач для начальной (без рассеивателей) постановки задачи. Согласно выражению (9), данные решения, а также геометрия задачи определяют один или несколько векторов-источников S . После задания величин S для моделирования рассеянного поля возможно использование стандартных пакетов прикладных программ, включая пакеты на основе FDTD-алгоритмов для численного решения уравнений (7), (8) конечно-разностными методами. Преимуществами SF подхода при FDTD-моделировании также являются отсутствие ошибок дискретизации для падающего поля, возможности задания поглощающих граничных условий только для рассеянного поля и уменьшения размеров расчётной области при относительно малых рассеивающих объектах [5, 7–9].

2.    Моделирование полейвблизи диэлектрической и металлической НЧ

Для оценки и сравнения точности FDTD-моделирования методами SF (основной метод, используемый в данной работе) и TF-SF были проведены вычислительные эксперименты для исследования ближнего поля одной НЧ. На рис. 1 и 2 приведены распределения квадрата модуля амплитуды электрического поля (здесь и ниже будем использовать относительные единицы, | E |²/| E0 |², где E0 – векторная амплитуда падающей на НЧ волны) вблизи трёхмерных сферических диэлектрической (рис. 1) и металлической (рис. 2) НЧ радиусом R = 40 нм. НЧ находятся в воздухе ( ε = 1), их центры совпадают с центром декартовой системы координат. На рис. 1, 2 также приведены для сравнения соответствующие кривые, полученные аналитическим методом (точное решение) на основе теории Ми [11, 12] (в областях вне НЧ). Для FDTD-моделирования (SF, TF-SF) использовался пакет Meep [10] и средства платформы удалённых параллельных вычислений nanoHUB [18, 19]. Различные кривые на рис. 1, 2 соответствуют изменению одной из координат при нулевых значениях двух других координат, т.е. рассматривается распределение поля в центральных сечениях сферической НЧ, параллельных координатным осям.

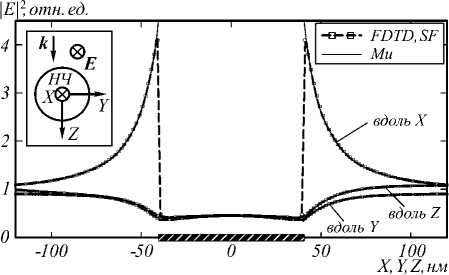
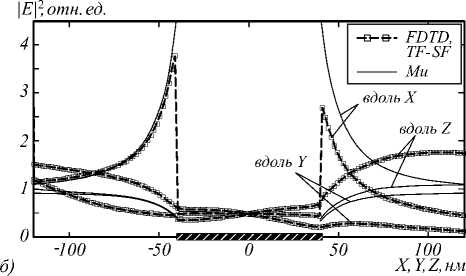
Рис. 1. Распределение нормированного квадрата модуля амплитуды электрического поля вблизи сферической диэлектрической НЧ в воздухе для направлений вдоль одной из координатных осей и центрального сечения НЧ. Расчёты выполнены по методам SF (а), TF-SF (б), согласно теории Ми (для областей вне НЧ; на (а), (б) приведены для сравнения одинаковые кривые). На вставке схематически показаны направление волнового вектора (параллельно оси Z) и TE-поляризация падающей волны для данных на (а), (б). Здесь и на рисунках ниже на оси абсцисс

выделена область, соответствующая расположению центрального сечения НЧ

\Е\-,отн. ед.

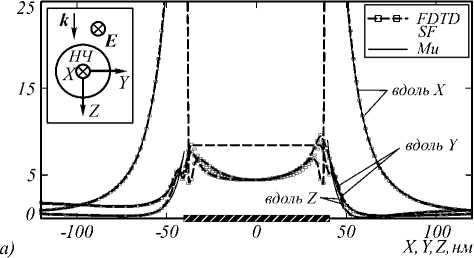
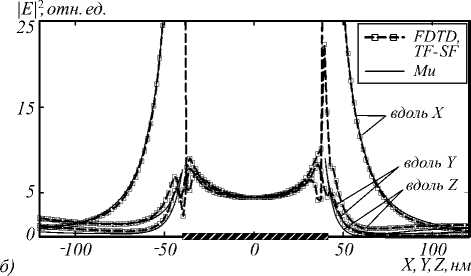
Рис. 2. Распределение нормированного квадрата модуля амплитуды электрического поля вблизи сферической металлической (Ag) НЧ в воздухе для направлений вдоль одной из координатных осей и центрального сечения НЧ.

Остальные данные аналогичны приведённым для рис. 1

Возбуждение осуществлялось плоской, линейно поляризованной вдоль оси X волной с длиной 405 нм. Моделирование проводилось до момента времени установления стационарного распределения поля в расчётной области. Выбирались значения диэлектрической проницаемости материала НЧ ε NP =3,5191 +0,5798 i (для данных на рис. 1, 3) и ε NP =–3,5191 +0,5798 i (для данных на рис. 2,4, соответствует серебру [20], причём при указанных размерах НЧ и условиях возбуждения могут иметь место локализованные плазмонные резонансы НЧ [11, 12, 15]). Характеристики серебряных НЧ, материалов вне НЧ и условий возбуждения для данных рис. 2, 4 выбирались в областях значений параметров, реализуемых для нанокомпозитов на основе высококремнезёмных золь-гель стёкол [13–15].

Для FDTD-моделирования использовалась пространственная расчётная область в форме куба с ребром 240 нм. После установления стационарного распределения поля результаты моделирования практически не зависели от толщины согласующего слоя (Perfectly Matched Layer, PML [2, 10]) вокруг расчётной области. Поэтому для ускорения расчётов использовался тонкий PML с толщиной 10 нм. Шаг пространственной сетки соответствовал разрешению 600 точек на 1 мкм (около 1,67 нм) в направлениях всех координатных осей.

Данные FDTD-моделирования на рис. 1 б и 2 б получены при реализации возбуждения плоской волной, заданием требуемого согласно методу TF-SF [2–4, 10, 21] распределения поля на границах расчётной области – на плоскостях x = –120 нм, y = –120 нм, z = –120 нм.

Согласно данным рис. 1, 2, при удалении от поверхности НЧ на расстояние порядка R в направлении вдоль одной из координатных осей относительная амплитуда электрического поля быстро уменьшается (увеличивается) до 1 для направлений, параллельных (перпендикулярных) полю E0 . Усиление ближнего поля в окружающей НЧ среде имеет место как для металлической (рис. 2), так и для диэлектрической (рис. 1) НЧ (в основном, для направлений, параллельных плоскости поляризации возбуждающего излучения). При этом максимальные значения | E |²/| E0 |²для серебряной НЧ на порядок и более превосходят аналогичные значения для диэлектрической НЧ.

Сравнение результатов моделирования с точным решением Ми (в области вне НЧ) показывает, что для диэлектрической НЧ (рис. 1) точность метода SF несколько выше, чем TF-SF. Для металлической НЧ (рис. 2) оба метода близки по точности при расчёте поля в направлении поляризации возбуждающей вол- ны (вдоль оси X). Для направлений, перпендикулярных поляризации возбуждающей волны, результаты метода TF-SF менее точны (рис. 2б). Такая погрешность TF-SF моделирования обусловлена (в числе прочего) особенностями реализации TF-SF в пакете Meep (введением источников в виде плоскостей, а не в численной формулировке [2]).

\Е\г,отн. ед.

б)

Из первой среды (воздуха, ε ₁ = 1) на НЧ падает линейно поляризованная (TH- или TE-) волна с длиной 405 нм, которая отражается и преломляется на границе раздела. Для второй среды (в области z >  R ) задана

3.    Моделирование полей вблизи НЧ: влияние плоской границы раздела

Для исследования влияния границы раздела двух диэлектрических сред на ближнее поле НЧ было выполнено моделирование по методу SF для расчётных областей и условий возбуждения, схематически показанных на вставках к рис. 3, 4.

\Е\2,отн. ед.

б)                                              X. К нм

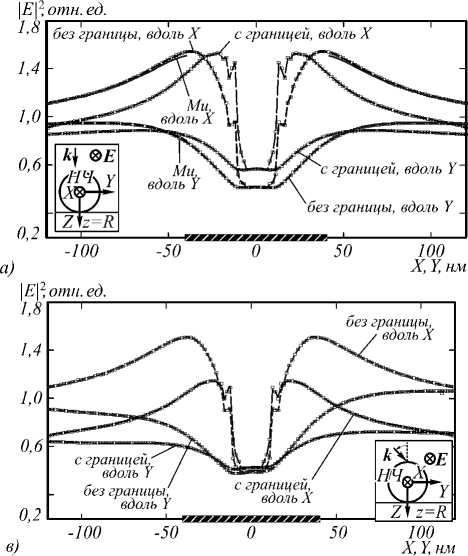
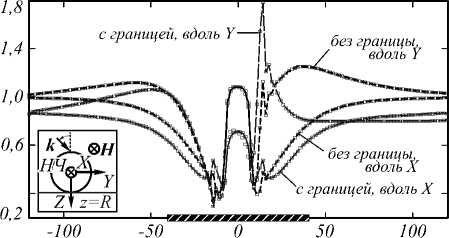
Рис. 3. Распределение нормированного квадрата модуля амплитуды электрического поля вблизи сферической диэлектрической НЧ на границе раздела z = R воздуха (область z < R) и диэлектрика ( z > R, ε ₂ = 2,4) для направлений вдоль одной из осей X, Y и центрального сечения НЧ. Моделирование выполнено по методу SF для нормального (а) и наклонного падения (угол падения 45º) возбуждающей волны с TH- (б) и TE- (в) поляризацией. На вставках схематически показаны направления волнового вектора и поляризации падающей волны. Для сравнения также приведены соответствующие кривые, полученные при отсутствии границы раздела, в том числе по теории Ми для области вне НЧ (а)

\Е^,отн.ед.

X. К нм

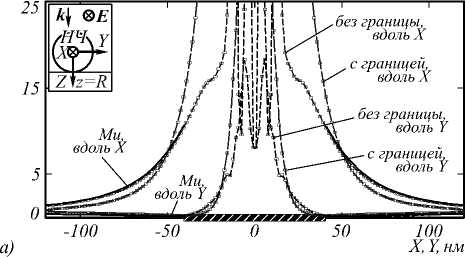
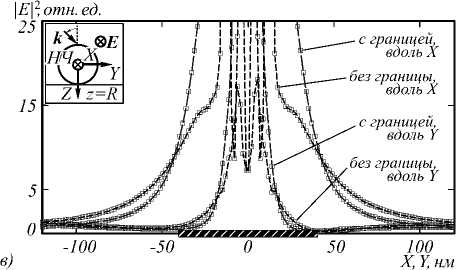
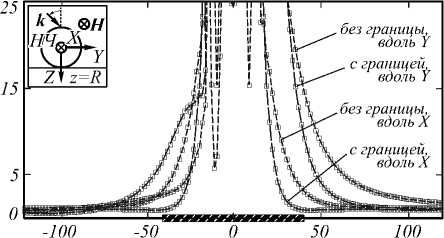
Рис. 4. Распределение нормированного квадрата модуля амплитуды электрического поля вблизи сферической металлической (Ag) НЧ на границе раздела z = R воздуха (z < R, ε ₁ = 1) и диэлектрика (z > R, ε ₂ = 2,4) для направлений вдоль осей X, Y и центрального сечения НЧ.

Остальные данные аналогичны приведённым для рис. 3

Предполагалось, что на границе раздела (плоскости z = R ) размещена диэлектрическая (рис. 3) или серебряная (рис. 4) НЧ с центром в начале координат и радиусом R =40 нм.

диэлектрическая проницаемость ε2 = 2,4, соответствующая диапазону характеристик высококремнезёмных золь-гель стёкол, применяемых для создания на-нокомпозитных материалов [13–15]. Отметим, что модельная структура «НЧ – плоская граница раздела диэлектриков» также может быть использована для исследования более сложных систем «НЧ – сферические микрочастицы кремнезёма (в составе аэросилов, силохромов)» [22–24]. Размеры таких микрочастиц могут существенно превышать 1 мкм, поэтому в области ближнего поля НЧ кривизна поверхности микрочастицы несущественна.

Исследовалось распределение ближнего поля на границе раздела вблизи НЧ для направлений вдоль одной из осей X , Y . Таким образом, данные на рис. 3, 4 соответствуют распределению величины | E |²/ | E0 |² при изменении координаты X (при y =0, z = R ) и при изменении координаты Y (при x =0, z = R ) в присутствии или отсутствие границы раздела.

Рассмотрим характерные особенности изменения локального поля вблизи НЧ, обусловленные влиянием границы раздела, на основе сравнения данных рис. 1 и 3 (для диэлектрической НЧ), рис. 2 и 4 (для металлической НЧ). Видно, что (как при наличии, так и при отсутствии границы раздела) возмущения ближнего поля, существенно отличающиеся по величине от поля падающей волны, имеют место, в основном, на расстояниях порядка 3 R от центра НЧ. При этом направление наибольшего изменения локального поля определяется направлением поляризации возбуждающей волны. Также можно отметить (для обоих типов НЧ) уменьшение в 2–4 раза интенсивности локального поля вне НЧ при переходе от плоскости центрального сечения НЧ (данные рис. 1, 2) к плоскости, касающейся НЧ (рис. 3, 4).

Диэлектрическая НЧ . В этом случае (рис. 3) появление границы раздела ведёт к монотонному (в зависимости от расстояния) уменьшению ближнего поля в направлении поляризации падающей волны вблизи поверхности НЧ (на расстояниях порядка R от поверхности НЧ). При этом значения величины | E |²/| E0 |² уменьшаются на 5-10% при нормальном падении (рис. 3 а ) и на 30-50% при наклонном падении (рис. 3 б , 3 в ). Для наклонного падения и направлений, перпендикулярных поляризации падающей волны ( X , Y для данных рис. 3 б и 3 в соответственно), величина локального поля также уменьшается с появлением границы раздела, но в меньших пределах (порядка 10%).

Серебряная НЧ. В этом случае (рис. 4) появление границы раздела ведёт к изменениям ближнего поля НЧ, качественно похожим на случай диэлектрической НЧ. Однако области максимального возмущения ближнего поля НЧ становятся гораздо больше – до расстояний порядка 2R от поверхности НЧ в направлениях поляризации возбуждающего излучения. Кроме того, в случае серебряной НЧ существенно возрастает отличие интенсивности локального поля для направлений вдоль и перпендикулярно поляризации падающей волны. Для направлений, перпендикулярных поляризации падающей волны, усиление локального поля практически отсутствует в области вне НЧ (рис. 4б) либо имеет место не усиление, а ослабление ближнего поля вблизи НЧ по сравнению с падающей волной (рис. 4а, 4в).

При нормальном падении появление границы раздела может вести как к усилению локального поля вблизи поверхности НЧ, так и к его ослаблению с ростом расстояния от НЧ (рис. 3 а , направление вдоль оси Y , рис. 4 а , направление вдоль оси X).

На рис. 5 приведена карта распределения величины | E |²/| E₀ |² в плоскости поляризации возбуждающей волны, включающей центральное сечение серебряной НЧ и границу раздела «воздух – золь-гель стекло». Рассмотрены случай касания НЧ границы раздела (рис. 5 а , эти данные дополняют результаты, приведённые на рис. 4 а ), а также случай наличия малого зазора R /10=4 нм между поверхностью НЧ и границей раздела (рис. 5 б ). Геометрию системы на рис. 5 б предлагается использовать для создания нанокомпо-зитных покрытий, являющихся эффективными плазмонными поглотителями света [25] (при выполнении ряда дополнительных требований к параметрам системы, ведущих к усилению магнитных мод НЧ). Сравнение данных рис. 2 и рис. 4 а , 5 показывает, что появление границы раздела вблизи поверхности серебряной НЧ (на расстояниях порядка нескольких нм) качественно модифицирует пространственное распределение ближнего поля НЧ.

a)           l_l 60           б)

Рис. 5. Карта распределения значений величины | E |²/| E₀ |² вблизи сферической серебряной НЧ на границе раздела воздуха ( £ 1 =1) и диэлектрика ( £ 2 =2,4) в плоскости поляризации падающей волны для центрального сечения НЧ: НЧ касается границы раздела (а); зазор между поверхностью НЧ и границей раздела равен 4 нм (б). На вставках схематически показаны направление волнового вектора и поляризация падающей волны (соответственно перпендикулярно и параллельно границе раздела)

Максимальное усиление локального поля имеет место не вблизи концов отрезка – диаметра НЧ, параллельного плоскости поляризации возбуждающей волны (что характерно для отдельной НЧ, рис. 1, 2), а вблизи точки касания НЧ и границы раздела (рис. 4 а , 5 а ) или зазора между НЧ и границей раздела (рис. 5 б ). При этом геометрия системы без зазора (рис. 5 а ) предпочтительнее для получения больших областей эффективного усиления ближнего поля, чем геометрия с зазором (рис. 5 б ).

Согласно данным рис. 5, наибольший линейный размер области (с центром в точке касания НЧ и границы раздела), соответствующей максимальному усилению локального поля (до значений |E|2/|E0|2 = 60 и более), можно оценить как (1^2) R в направлении поляризации возбуждающего излучения. В направлении, перпендикулярном плоскости поляризации падающей волны, область максимального усиления ближнего поля имеет меньшие размеры: порядка R и менее (рис. 4, это также подтверждается данными, аналогичными рис. 5 для этого случая, которые здесь не приводятся). Можно предположить, что именно в этой области (причём как на границе раздела, так и вне её) целесообразно размещение различных фотоактивных центров (молекул, квантовых точек) для приложений нано-плазмоники, использующих металлические НЧ в качестве «генераторов» больших локальных полей вблизи границ раздела диэлектриков.

4.    Оценка влияния наличия плоской границы раздела на поле вблизи НЧ

Предположим, что сферическая НЧ радиуса R с центром в начале координат и некоторые поглощающие (пробные) центры (например, фотоактивные центры, молекулы, квантовые точки) расположены на участке плоской поверхности W (границы раздела двух сред), характеризуемой уравнением z — R в декартовой системе координат. При моделировании электромагнитных полей методом конечных разностей используется разбиение пространственной счётной области с помощью прямоугольной трёхмерной сетки. С учётом этого определим коэффициент K, по- зволяющий оценить «в среднем» влияние заданного участка поверхности W на интенсивность поля вблизи НЧ, следующим образом:

2 ,

где x , y , z – координаты узла сетки, лежащего на поверхности W , E ( x , y , z ) и E _re f ( x , y , z ) – полученные в результате моделирования напряжённости электрического поля вблизи НЧ в присутствие и отсутствие границы раздела W соответственно. В выражении (15) в качестве участка поверхности W выбран квадрат со стороной, равной 2 a , симметрично расположенный относительно НЧ, N – количество расчётных точек на этом участке поверхности. Согласно данным графического анализа, приведённым выше (рис. 3–5), размеры области, где рассеянное НЧ поле вносит основной вклад в полное поле вблизи поверхности W , можно оценить условием 2 a <  6 R .

Таким образом, значение коэффициента К показывает, насколько интенсивность поля вблизи НЧ и границы раздела, определяющая вероятность поглощения излучения фотоактивными центрами, размещёнными вне НЧ на поверхности W , изменяется в среднем на заданной квадратной области при появлении плоской границы раздела двух однородных сред в области ближнего поля НЧ.

С использованием метода SF оценено влияние границы раздела двух диэлектрических сред на распределение поля вблизи диэлектрической и металлической НЧ. Результаты расчётов при выборе значений 2 a — 6 R , 4 R , 3 R приведены в таблице ниже. При проведении расчётов использовались следующие значения параметров, не указанных в таблице: радиус НЧ R =40 нм, первая среда - воздух ( £ 1 = 1), вторая среда -высококремнезёмное золь-гель стекло ( £ 2 = 2,4), для всех случаев бралось Im( £ NP )=0,5798 (изменялась вещественная часть диэлектрической проницаемости материала НЧ, Re ( £ _NP )), возбуждение осуществлялось плоской, линейно поляризованной волной с длиной 405 нм.

Таблица. Значения коэффициента К в зависимости от параметров моделируемой системы

Тип НЧ	Re( e np )	Поляризация	Угол падения	Коэффициент влияния поверхности K
				2 a — 6 R	2 a — 4 R	2 a — 3 R
Метал-личе-ская	–2,5	–	0	1,1578	1,2450	1,4657
	–3	–	0	1,1681	1,3207	1,5989
	–3,51	–	0	1,1707	1,4777	1,9106
	–5,5	–	0	1,1080	1,4731	1,9122
	–3,51	TE	45º	0,8548	1,0779	1,3870
	–3,51	TM	45º	0,7862	0,9120	1,1063
Диэлек-тричес-кая	2,5	–	0	0,8983	0,9206	0,9506
	3	–	0	0,8992	0,9270	0,9642
	3,51	–	0	0,9006	0,9338	0,9779
	5,5	–	0	0,9069	0,9566	1,0211
	3,51	TE	45º	0,6962	0,7244	0,7617
	3,51	TM	45º	0,8407	0,8449	0,8542

Как видно из таблицы, появление границы раздела может как усиливать (K > 1), так и ослаблять (K < 1) поле вблизи НЧ. Для диэлектрической НЧ изменение поля небольшое: |K–1| ≤ 0,1 при нормальном падении, |K– 1| ≤ 0,3 при наклонном падении (угол падения 45º). Для такой НЧ при наклонном падении наличие границы раздела оказывает более существенное влияние и, по-видимому, в большинстве случаев ослабляет локальное поле на границе раздела вблизи НЧ. Также видно, что уменьшение площади участка поверхности, влияние которого исследуется, от 36R2 до 9R2 ведёт к небольшому (порядка 10%) увеличению значений К.

Для металлической НЧ характерно существенное усиление влияния границы раздела с уменьшением площади участка поверхности (до значений | K –1| ≤ 0,9 для данных таблицы). Видно, что и в этом случае усиление локального поля максимально при нормальном падении возбуждающего излучения.

Отметим, что данные таблицы учитывают вклад в усиление локального поля как участков поверхности, близких к центральному сечению НЧ (параллельному плоскости поляризации падающей волны), где значения К гораздо больше приведённых в таблице (см. данные рис. 4, 5), так и вклад других участков области поверхности с меньшими (близкими к 1) значениями К . Приведённые данные дополняют результаты графического анализа (раздел 4) и подтверждают сделанные оценки размеров области на границе раздела вблизи НЧ, соответствующей наиболее эффективному усилению поля: 2 a ≤ 3 R и 2 a ≤ R для направлений соответственно вдоль и перпендикулярно поляризации возбуждающего излучения.

Заключение

Результаты выполненного моделирования и графического анализа позволяют уточнить ряд аспектов, связанных как с методикой FDTD-моделирования, так и с исследованием характеристик локального оптического отклика рассматриваемых наноструктур.

Сравнение данных моделирования, полученных по методикам TF-SF и SF, с точным решением Ми (раздел 2) показывает, что точность методики SF для исследованных геометрий задач и значений параметров оказывается выше, чем TF-SF (в частности, существенно выше для диэлектрических НЧ).

Исследовано изменение характеристик усиления ближнего поля диэлектрической и металлической НЧ в воздухе, обусловленное наличием границы раздела двух диэлектриков (воздух – высококремнезёмное золь-гель стекло) в области ближнего поля НЧ (разделы 2, 3). Показано, что (как при наличии, так и при отсутствии границы раздела) возмущения ближнего поля НЧ по сравнению с полем падающей волны имеют место, в основном, на расстояниях порядка 3 R от центра НЧ. При наличии границы раздела область максимального усиления локального поля находится вблизи точки касания НЧ и границы раздела или зазора между НЧ и границей раздела. Для серебряной НЧ размеры данной области на границе раздела можно оценить как (1 + 2) R и R для направлений параллельно и перпендикулярно плоскости поляризации возбуждающей волны соответственно.

В разделе 4 предложена простая методика оценки влияния границы раздела на характеристики ближнего поля НЧ и показано, что появление такой границы может, в среднем, как усиливать, так и ослаблять локальное поле НЧ. Данные изменения поля невелики для диэлектрических НЧ и могут быть существенны для металлических НЧ, особенно в случае нормального падения возбуждающего излучения на систему «НЧ – граница раздела двух диэлектриков».

Полученные результаты также могут быть использованы для оптимизации характеристик нанокомпозитов «высококремнезёмные золь-гель стекла – НЧ благородных металлов» для приложений оптики и наноплазмоники [13 – 15].

Работа выполнена при поддержке программы ГКПНИ «Функциональные и машиностроительные материалы, наноматериалы» (задание 2.4.02.01) Республики Беларусь.