Применение метода «сдвига среднего» (mean shift) для обработки металлографических изображений

Применение метода сдвига среднего (mean shift) [1] для анализа изображений микроструктур сплавов обладает тем преимуществом, что для его работы не требуется никаких дополнительных знаний об изображении и количестве формируемых кластеров. Метод mean-shift обладает следующими достоинствами:

• •    масштабируемость (время работы линейно зависит от количества обрабатываемых точек);

• •    робастность (процедура даёт устойчивые результаты при изменении входных параметров);

• •    возможность параллельной обработки.

Тем не менее, метод обладает и недостатками.

• 1.    Чувствительность к размерам окна.

• 2.    Значительное увеличение времени работы алгоритма при росте размеров окна

Единственным параметром кластеризации методом mean shift является размер окна h в пространстве признаков. При анализе цветных изображений этот параметр представляется в виде вектора в d-мерном пространстве признаков. Значения составляющих этого вектора оказывают существенное влияние на результаты сегментации. Существует большое количество методик выбора размера окна на основе статистических данных об изображении. Это позволяет избавиться от необходимости подбирать размеры окна экспериментально, но не решает саму проблему сильного влияния значений параметров на результаты сегментации притом, что форма их зависимости неоднозначна. Поэтому необходимо выбирать размер окна h при настройке алгоритма на работу с конкретными данными, при этом часто для каждой координаты выбирается собственный размер окна, что так же усложняет настройку процедуры.

Последний пункт имеет особое значение в виду того, что размер окна влияет на количество получаемых в результате кластеризации областей, причём, чем больше размер окна, тем меньше кластеров будет получено, а именно небольшое количество кластеров, как правило, является целью кластеризации. Впрочем, этот недостаток может быть устранен применением систем параллельных вычислений.

Применение алгоритма mean-shift, предполагает использование агломеративной (иерархической) стратегии, то есть проведение кластеризации изображения в несколько этапов. При этом кластеры последовательно формируются до окончательного построения замкнутых областей, отображающих компоненты входящие в сплав.

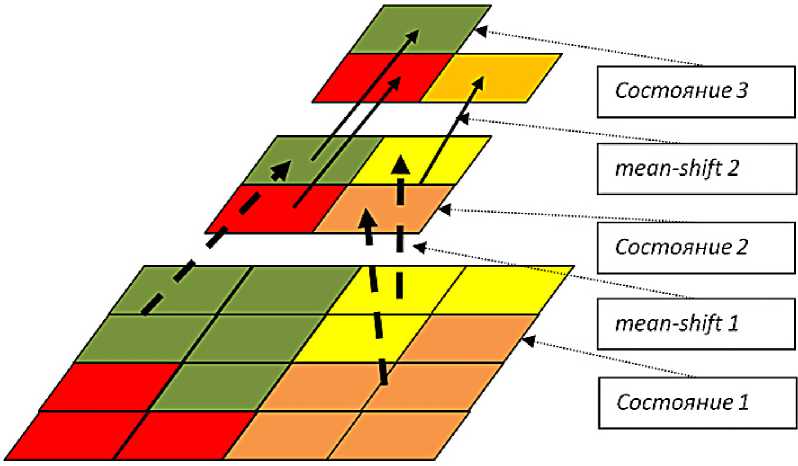
Рис. 1. Механизм агломеративной кластеризации

На рис. 1 представлена общая схема агломеративной кластеризации, где каждый следующий этап кластеризации работает с набором точек, состоящим из центров кластеров предыдущего этапа.

Здесь, состояние 1 – это исходный набор точек, состояние 2 – это набор, состоящий из центров кластеров, полученных в результате среднего сдвига 1, и т.д. Первый этап среднего сдвига использует небольшой размер окна, что сокращает время работы. Каждый следующий этап работает с большим размером окна, но со значительно меньшим количеством точек, что также сокращает время работы. Как итог общее время работы сокращается.

При использовании такой стратегии выполняется несколько процедур сдвига среднего, а значит необходимо для каждой из них подбирать размер окна h . Кроме того этот размер должен постоянно увеличиваться. Для этого можно воспользоваться алгоритмом, предложенным в работе [2].

Предложенный метод состоит в ограничении всего набора точек гиперпараллелепипедом с объёмом V и разбиению его на n субпараллелепипедов с объёмом:

где n количество точек.

То есть, если все точки были бы распределены по пространству равномерно, то каждая находилась бы в своём гиперпараллелепипеде с объёмом V_m , Соответственно, стороны гиперпараллелепипеда и будут определять размеры окна, то есть параметр h . Иными словами размер окна для i -го измерения будет определяться по формуле:

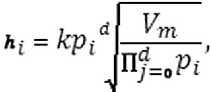
где p_i – коэффициент компоненты, который определяется пропорционально сторонам основного гиперпаралле-

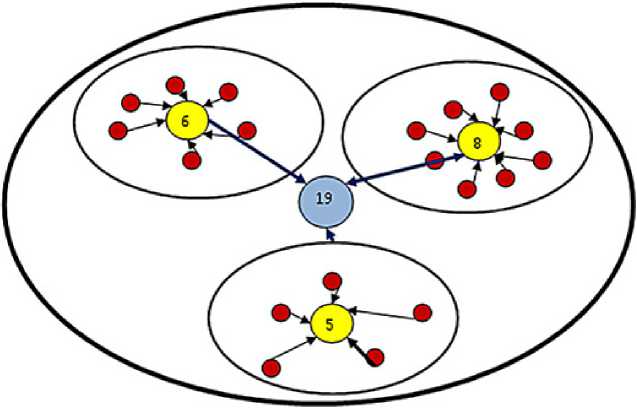
Рис. 2. Схема объединения кластеров

лепипеда, d – размерность пространства, k – коэффициент, вводимый для того, чтобы иметь возможность управлять количеством формируемых кластеров.

Такой подход позволяет автоматически выбирать размер окна исходя из обрабатываемых данных. Этот метод не использует каких-либо предположений о природе исходных данных или о виде их распределения. В предложенном методе возможно использование поправочных коэффициентов для управления процессом кластеризации. Коэффициенты подбираются под определённые координаты, с целью увеличить или уменьшить их важность при формировании кластера.

По мере уменьшения количества точек, вследствие кластеризации, размеры окна будут расти, что является необходимым условием для реализации агломеративной стратегии.

Кластеры, собравшие больше точек на определённом этапе, должны иметь преимущество на следующем этапе, для этого вводится понятие «веса точки», которая выступает сомножителем в арифметических операциях. «Вес точки»

вычисляется исходя из количества точек первого уровня, собранных в кластере, центром которого является текущая рассматриваемая точка. Это проиллюстрировано на рис. 2.

На первом этапе кластеризации выделяется три кластера. Следующий этап работает уже с 3-мя точками, Эти точки неравноправны, больший вес имеет та, в которую пришло больше точек. Соответственно, на следующем этапе все три точки были объединены в одну, с суммарным «весом» равным девятнадцати.

Таким образом, алгоритм кластеризации можно представить следующим образом: на первом этапе производится стандартная кластеризация методом mean shift с небольшим размером окна; затем вычисляется мощность каждой точки, являющейся центром кластера, и из этих точек формируется новый набор; затем снова производится кластеризация стандартным методом mean shift полученного набора. Последние три этапа повторяются до тех пор, пока кластеры не перестанут объединяться.