Применение метода сопряженных градиентов для эффективного управления промышленным предприятием

Экономика России находится в переходном состоянии от командно-административной системы к свободному рынку через вступление в ВТО [1]. В этих условиях от эффективности управления промышленным предприятием как сложной системой зависит экономическая безопасность его функционирования.

Под эффективностью в отечественной литературе [2] понимается “комплексное операционное свойство (качество) процесса, характеризующее его приспособленность к достижению цели операции (выполнению задачи системы)”. Эффективное управление открывает путь к гибкому планированию и самоуправлению [3].

В зарубежной литературе методика эффективного управления известна под названием “Шесть сигм”. “Шесть сигм” – это гибкая система совершенствования делового лидерства и показателей эффективности. Это не теория, а образ действия, способствующий постоянному успеху. Благодаря заимствованию инструментов и идей из разных дисциплин, система “Шесть сигм” позволяет улучшать не только результаты, но и сам процесс совершенствования [4].

Важными достижениями современной математической теории производства являются: моделирование процесса производства с помощью производственных функций; моделирование и оптимизация процесса мате- риально-технического снабжения на основе функций издержек; моделирование и описание процесса реализации путем решения задач рациональной коммерческой деятельности и другие. Необходимость разработки новых методов и моделей для принятия решений по управлению предприятием обусловлена тем, что существующие методы не дают наглядной обзорной картины экономического поведения предприятия в широком поле изменения переменных. Для динамичных объектов управления должен быть разработан инструментарий динамичного контроля изменения текущего состояния с обязательным измерением возникших отклонений от нормального движения и определением количественных уровней необходимых корректирующих действий.

В качестве основных характеристик результатов принятых к реализации решений, описывающих свойство устойчивости, предлагается [10] чувствительность и эластичность их к изменению параметров рыночной конъюнктуры. При первичной разработке бизнес-ситуации используются все факторы, оказывающие влияние на расходы и доходы предприятия (в количественном выражении). Анализ чувствительности позволяет определить степень важности отдельных факторов в формировании целевой функции и игнорировать те из них, которые не оказывают особого влияния на результат производственной деятельности.

В основе анализа чувствительности результатов по разнообразным связям между параметрами внешней среды и результатами принятых решений лежит, таким образом, использование коэффициентов (функций) чувствительности, представляющих собой градиенты показателей стратегии, принятой к реализации, по совокупности параметров, характеризующих внешнюю среду. Экономико-математические методы оптимизации и анализа позволяют обеспечить выработку оптимального решения с одновременным обоснованием его в условиях изменяющейся конъюнктуры рынка.

В результате многопараметрического анализа чувствительности прибыли необходимо выбрать достоверную (значимую) эконометрическую модель, основные факторы или их комплексы, наиболее сильно влияющие на целевую функцию исследования. Метод системного исследования должен быть направлен на оптимизацию уровня затрат в сферах проектирования, производства и эксплуатации изделий предприятия. Конечной целью данного исследования является разработка методики ежеквартального нахождения нового оптимального решения, применение которого сделает промышленное предприятие приемлемым для потребителей и производителей.

Постановка задачи эффективного управления

Для решения проблемы качественного управления предприятием необходимо построить его экономическую информационную модель. Создание модели процесса может происходить в двух аспектах. Первый основан на методах математической экономики, а второй – на методах эконометрики [5]. Среди моделей математической экономики можно выделить два крупных класса: модели равновесия в экономических системах (Эрроу-Дербе, В. Леонтьева) и модели экономического роста (Харрода-Домара, Солоу, магистрального типа). В основе эконометрических моделей (К. Пирсона, В. Парето, Р. Фишера, Кобба и Дугласа) лежит корреляционно-регрессионный анализ [5].

В последнее время два аспекта моделирования все чаще объединяются в общее направление: целевая функция формируется на основе эконометрического анализа, а исследование ее свойств проводится традиционными аналитическими методами. Современная математическая теория производства должна базироваться на моделях, достаточно полно описывающих черты реальной производственной деятельности и допускающих аналитическое решение [6].

Основными этапами оценивания эффективности управления промышленным предприятием могут быть следующие [2]:

• 1.    Определение цели оценивания.

• 2.    Измерение свойств сложной системы, признанных существенными для целей оценивания.

• 3.    Обоснование предпочтений – критериев качества и критериев функционирования предприятия.

• 4.    Собственно оценивание.

К задачам анализа процесса эффективности обычно относятся [2]:

• -    оценка эффективности процесса по выбранному критерию;

• -    анализ чувствительности показаний к изменению параметров;

• -    исследование направленности и степени влияния факторов на показатели эффективности процесса;

• -    выбор параметров, наиболее существенным образом влияющих на показатели эффективности процесса.

К задачам синтеза процесса эффективности относятся [2]:

• -    определение закона изменения структуры системы управления в зависимости от условий ее изменения;

• -    определение закона управления системой через ее параметры;

• -    выбор вида расходного ресурса и создание системы обеспечения хранения и восполнения ресурсов;

• -    выработка требований к параметрам и показателям качества системы в зависимости от условий ее функционирования.

Управление по системе “Шесть сигм” основано на “измерении” – отслеживании результатов работы компании и последующем сопоставлении этих показателей с источником целей по достижению идеального качества работы. Главной целью становится динамическое программирование: постоянное изменение интереса, формирование изменения целевой функции на основе ключевых критериев, выбранных методов анализа ключевых переменных из факторного пространства и оптимизация результатов [7].

Для формирования целевой функции необходимо описать интегрированную экономико-математическую модель, которая представляет собой комплексную проблему, для решения которой следует решить ряд задач математического моделирования, стандартную задачу линейного программирования или задачу нелинейного программирования.

Эконометрическая модель целевой функции управления

На этапе формулирования модели целевой функции убытков Y были выбраны управляемые переменные из статей бухгалтерского баланса предприятия (годовые и квартальные отчеты об экономической и финансовой деятельности). В настоящей модели это: х₁ – основные средства и нематериальные активы; х₂ – незавершенное строительство; х₃ - финансовые вложения; х₄ – запасы, х₅ – налог на добавленную стоимость по приобретенным ценностям; х₆ – дебиторская задолженность; х₇ – денежные средства; х₈ – сумма прочих внеоборотных и оборотных активов; х₉ – уставный капитал; х₁₀ – добавочный капитал, фонд социальной сферы, нераспределенная прибыль прошлых лет, резервы предстоящих расходов и прочие краткосрочные обязательства; х₁₁ – резервный капитал; х₁₂ – целевые финансирование и поступления; х₁₃ – нераспределенная прибыль (непокрытый убыток) отчетного года; х₁₄ – займы, кредиты и прочие долгосрочные обязательства; х₁₅ – кредиторская задолженность; х₁₆ – задолженность перед участниками по выплате доходов и доходы будущих периодов.

На этапе параметризации модели были проведены качественная оценка влияния переменных х1,...,х16 на целевую функцию Y и предварительный выбор определяющих ее факторов. Для этого в среде MS Excel выполнены корреляционный, регрессионный и дисперсионный анализы. Используя корреляционную таблицу, по уровню коэффициента корреляции, были выявлены основные факторы, коэффициенты корреляции которых с функцией Y по модулю больше 0,5. На основе регрессионного анализа были проверены на адекватность линейные уравнения множественной регрессии убытков на различные комбинации факторов с использованием коэффициента детерминации R2. Дисперсионный анализ проводился с помощью оценки уровня значимости критериев Фишера-Сне-декора (F) и Стьюдента (t–статистика). В результате были получены два уравнения целевой функции убытков:

Y1 = - 517832 + 2,302х4 + 25,108х5 +

+ 1,264х₁₃ - 1,584х₁₄, (1)

Y₂ = - 473304 + 1,671х₄ + 20,371х₅ - 0,485х₇+ +1,527х₁₃ - 1,276х₁₄ + 0,732х₁₅. (2)

Выделенные шесть факторов х₄, х₅, х₇,х₁₃,х₁₄,х₁₅ достаточно полно по коэффициенту детерминации R²> 0,9 объясняют причинно-следственную зависимость результатов процесса производства Y . Но, к сожалению, ни один из вариантов уравнений (1) и (2) не удовлетворяет требованиям адекватности модели либо по критерию Фишера-Сне-декора и уровню его значимости ( р- значение должно быть меньше 0,05) [8], либо по критерию Стьюдента ( t- статистика). Поэтому было принято решение перейти к более сложным нелинейным моделям.

Важное место при формировании нелинейной целевой функции убытков занимает определение эластичности этой функции, показывающей степень влияния выбранных факторов на Y [8]. В четырехфакторной линейной модели (1) коэффициенты эластичности оказались равными E4y = 19,890, E5y = 7,219, E13y = -0,230, E14y = -10,882. Таким образом, фактор х4 имеет положительную эластичность, фактор х14 – отрицательную, а эластичность фактора х13 близка к нулю. После- днее означает, что степень влияния фактора х13 весьма мала, и его влияние можно не учитывать в нелинейной модели.

В шестифакторной линейной модели (2) коэффициенты эластичности равны E₄^y = 14,436, E₅^y = 5,858, E₇^y = 0,623, E₁₃^y = -0,286, E₁₄^y = -8,766, E₁₅^y = 4,084 . Здесь эластичность факторов х₄, х₅, х₁₄ осталась практически на прежнем уровне, а эластичность факторов х₇ и х₁₃ незначительна.

Проведенное исследование эластичности линейной целевой функции убытков Y конкретного промышленного предприятия показало, что в первом приближении нелинейная модель может быть построена по двум факторам: х₄ и х₁₄ , которые оказывают наибольшее влияние на исследуемую функцию.

Оценка параметров уравнения множественной нелинейной регрессии функции убытков Y проводилась с помощью табличного процессора MS Excel (“Анализ данных” - “Регрессия”). Рассматривая различные комбинации факторов х₄, х₁₄ и их степени, были получены несколько нелинейных уравнений целевой функции убытков Y :

• Y 3 = -156734 + 9,62⋅10-6х42 + +6,1⋅10-30х46 - 2⋅10-5х4х14 + +1,34⋅10-5х142 - 6⋅10-12х143,(3)

• Y 4 = -138024 + 8,58⋅10-6х42 + +1,08⋅10-5х142 - 1,7⋅10-5х4х14 + +6,28⋅10-30х46 - 6,4⋅10-18х144,(4)

• Y 5 = -134508 + 8,53⋅10-6х42+ + 1,11⋅10-5х142 - 1,8⋅10-5х4х14 + +4,91⋅10-24х45 - 6,8⋅10-18х14,(5)

Y6 = -154137 + 9,6⋅10-6х42 + +1,38⋅10-5х142 - 2⋅10-5х4х14 + + 4,81⋅10-24х45 - 6,5⋅10-12х143.(6)

В табл. 1 представлены характерные результаты эконометрического анализа целевой функции убытков Y₄ . Все четыре нелинейные формы (3)...(6) удовлетворяют сразу трем критериям: R²>0,9 , F и t ( p -значение меньше 0,02).

В уравнениях (3)...(6) чувствительность функции убытков Y к комплексам факторов изменяется в очень узких диапазонах: –(134508…156734) – для свободного члена; (8,53…9,62) ⋅ 10^-6 – для х₄² ; (4,81…4,91) ⋅ 10^-24 – для х₄⁵ ; (6,10…6,28) ⋅ 10^-30 – для х₄⁶ ; –(1,7…2,0) ⋅ 10^-5 – для х₄х₁₄ ; (1,08…1,38) ⋅ 10^-5 – для х₁₄² ; –(6,0…6,5) ⋅ 10^-12 – для х₁₄³ ; –(6,4…6,8) ⋅ 10^-18 – для х₁₄⁴ .

На рис. в среде Maple 9.5 показаны сра-

Таблица 1. Характерные результаты эконометрического анализа целевой функции убытков

Вывод итогов по двум факторам

Регрессионная статистика
Множеств. R2	0,971426
R-квадрат	0,943669
Нормир. R2	0,92355
Станд. ошибка	54125,93
Наблюдения	20
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	5	6,87E+11	1,37E+11	46,90586	2,97E-08
Остаток	14	4,1E+10	2,93E+09
Итого	19	7,28E+11
	Коэффициенты	Станд. ошибка	t-статис тика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	-138024	37205,96	-3,70973	0,002332	-217823	-58225,0334	-217822,863	-58225,03343
X4^	8,58E-06	2,4E-06	3,579004	0,003022	3,44E-06	1,37268E-05	3,43952E-06	1,37268E-05
X14^	1,08E-05	2,24E-06	4,816453	0,000274	5,99E-06	1,5608E-05	5,99021E-06	1,5608E-05
X4*X14	-1,7E-05	4,3E-06	-4,06747	0,001153	-2,7E-05	-8,26E-06	-2,66884E-05	-8,26002E-06
X4^6	6,28E-30	2,25E-30	2,78731	0,014539	1,45E-30	1,11206E-29	1,44872E-30	1,11206E-29
X14^4	-6,4E-18	1,76E-18	-3,60639	0,002862	-1E-17	-2,5769E-18	-1,01397E-17	-2,57689E-18

зу все четыре нелинейные формы Y3…Y6 целевой функции убытков промышленного предприятия. Из рис. видно, что в исследуемой области х4,х14∈[0;106 тыс. руб.] формы отличаются незначительно. Это свидетельствует о том, что все перечисленные нелиней- ные уравнения практически равноценны и могут быть использованы для построения процедуры минимизации функции убытков. Показатели степени факторов х4, х4х14 и х14 в указанных уравнениях составляют 2…6; 1 и 2…4 соответственно, то есть суммарная эластичность в уравнениях по факторам не превышает 11.

Поверхности (3)...(6) на рис. представляют собой “овраг” с достаточно крутыми “склонами” и поэтому движение к минимуму убытков (“дно оврага”) должно проходить в “овражной ситуации” строго по оптимальной траектории. “Овраг” имеет “пологое дно” в области начала координат. Вдоль биссектрисы первой четверти системы координат Ох4х14Y при увеличении факторов х4 и х14 убытки Y уменьшаются, однако, слева и справа от нее резко возрастают. Это может привести к неустойчивому состоянию экономи- ки предприятия, так как резкое изменение соотношения факторов х4 (запасы) и х14 (займы, кредиты) приводит к переходу с одного “склона оврага” на другой и соответственно к состоянию банкротства предприятия.

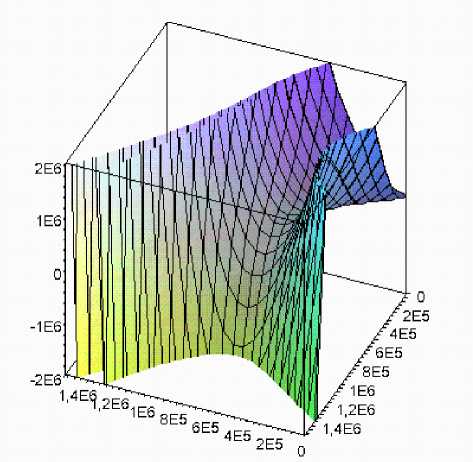
Рис. Четыре нелинейные формы целевой функции убытков промышленного предприятия