Применение метода термоупругости при конечно-элементном моделировании остаточного напряжённого состояния в поверхностно упрочнённых деталях

чальных деформаций не удовлетворяют условиям совместности Сен-Венана [2]. Следовательно, в сплошной среде эти деформации не могут быть реализованы, так как в нём могут существовать и находиться в равновесии только совместные деформации. Таким образом, после появления первоначальных деформаций в теле возникают препятствующие нарушению условий сплошности силы, составляющие само-уравновешенное поле собственных напряжений. Такие напряжения называются остаточными и им соответствуют деформации, которые измеряются на практике с помощью различных методов и способов. При этом считается, что остаточные напряжения не превышают предела текучести материала и вызванная ими деформация является упругой.

Если необратимые линейные изменения тела во всех направлениях будут одинаковыми, то возникает объёмная деформация, имеющая много общего с температурной деформацией. Использование этой связи первоначальных деформаций с термоупругостью материала и позволяет использовать современные расчётные комплексы, реализующие метод конечных элементов в форме перемещений, при решении задач о распределениях остаточных напряжений в поверхностно упрочнённых деталях сложной формы.

В качестве примера приведём решение задачи по расчёту остаточных напряжений в поверхностном слое сплошного цилиндра с первоначальной изотропной объёмной деформацией, постоянной по всем направлениям. Аналитическое решение этой задачи приведено в работе Бирге- ра И.А. [1], которое основано на использовании следующих уравнений теории упругости, записанных в цилиндрической системе координат:

,(1)

,(2)

,(3)

где         – радиальные, окружные и осевые остаточные напряжения;

– радиальные, окружные и осевые первоначальные деформации;

– модуль продольной упругости материала; – коэффициент Пуассона.

Данное решение выполнено для той части цилиндра, в которой исключается влияние краевых зон. Эскиз цилиндра приведён на рис. 1.

В поверхностном кольцевом слое цилиндра толщиной 8 = b - c имеется остаточная первоначальная деформация

£0г — £ое — ^ — ^^

Для расчёта были приняты следующие численные значения параметров:

b = 5 мм; c = 4,5 мм; E = 200 000 МПа; Ц = 0,3;

= 0,001.

Остаточные напряжения в цилиндре в пределах внутренней области цилиндра определяются по формулам

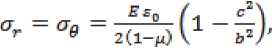
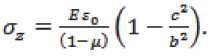
По результатам подстановки численных значений параметров в уравнения (4) и (5) получе- ны следующие значения остаточных напряжений:                             ,                     .

В поверхностном слое цилиндра остаточные напряжения определяются по фор- мулам

°r 2(1—м) \г2   Ь1/' Ее0 ( 1    1	(6)
^     2(1-д)1г= 1 Ь2/'	(7)
Esd с3
а=      (1-м) ь2’	(8)

По результатам подстановки численных значений параметров в уравнения (6) – (8) были получены следующие значения остаточных напряжений в поверхностном слое цилиндра:

,                                                                  .

Для решения задачи численным методом был использован расчётный комплекс PATRAN/ NASTRAN. Конечно-элементная модель в осесимметричной постановке представляет собой осевое сечение четверти цилиндра с наложением соответствующих граничных условий. Принятая длина расчётной области цилиндра исключает влияние краевых зон для сечения, в котором значения компонент остаточных напряжений сравниваются с их значениями для случая аналитического решения. При моделировании был использован треугольный шестиузловой осесимметричный конечный элемент типа 2DSolid. Первоначальная деформация в поверхностном слое моделировалась как температурное расширение тела, при этом коэффи циент линейного расширения = 0,00001    , грай перепад температуры относительно внутренней области составлял AT = 100 oC.

Результаты расчётов распределения остаточных напряжений по поперечному сечению цилиндра аналитическим и численным методами в виде графиков представлены на рис. 2 – 4. На графиках отсчёт оси y производился от поверхности к оси цилиндра (рис. 1).

Из приведённых на рис. 2– 4 распределений остаточных напряжений видно, что аналитический и численный методы дают одинаковые результаты, поэтому метод термоупругости может применяться для моделирования остаточных напряжений в поверхностно упрочнённых деталях.

Использование расчётного комплекса

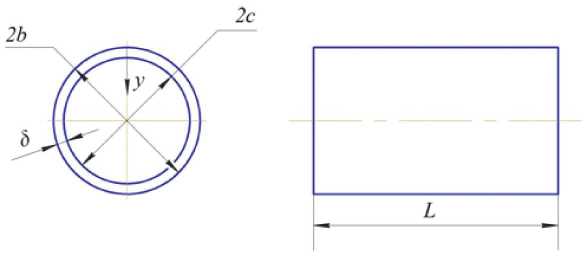
Рис. 1. Эскиз цилиндра с первоначальными деформациями

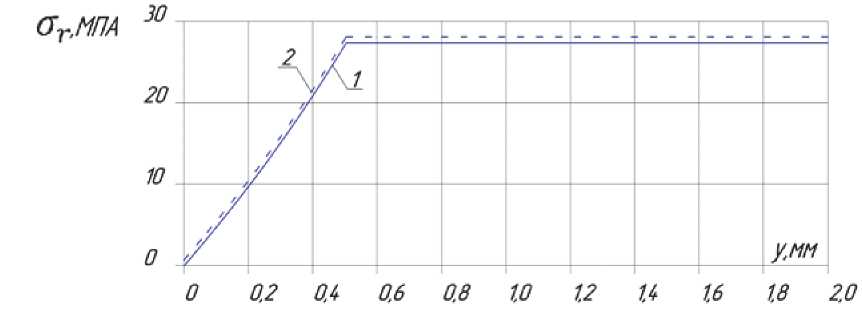
Рис. 2. Распределение радиальных a остаточных напряжений по сечению цилиндра: 1 – аналитическое решение, 2 - МКЭ

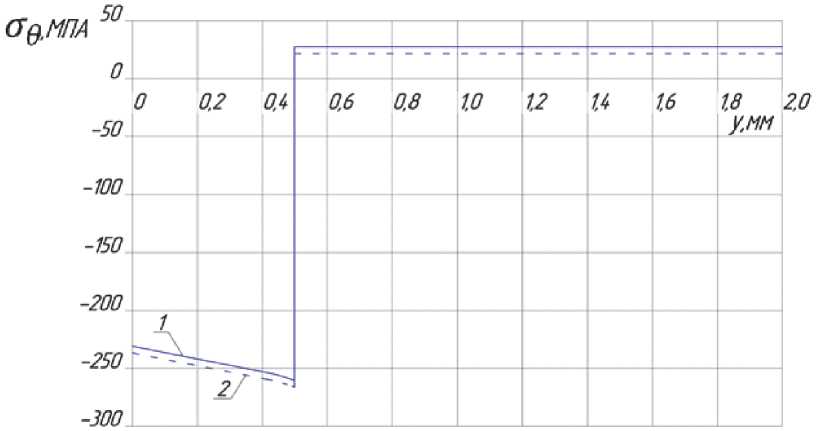
Рис. 3. Распределение окружных tJg остаточных напряжений по сечению цилиндра: 1 – аналитическое решение, 2 - МКЭ

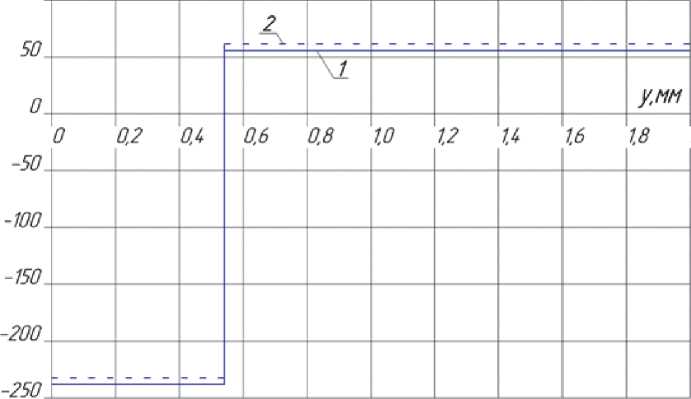
Рис. 4. Распределение осевых tJ остаточных напряжений по сечению цилиндра: 1 – аналитическое решение, 2 – МКЭ

PATRAN/NASTRAN позволяет решать методами термоупругости задачи расчёта распределения остаточных напряжений и для случаев, когда первоначальные деформации по направлениям имеют различные значения (в том числе и знаки). Для этого в конечно-элементных моделях необходимо применять 3D-ортотропный материал, у которого механические характеристики (модули продольной и поперечной упругости, коэффициенты Пуассона) по всем направлениям системы координат одинаковые, а коэффициенты линейного расширения о; по этим направлениям имеют различные значения, то есть

,

,

£0я = az " ^ , где aT,aQ,az - коэффициенты линейного расширения в радиальном, окружном и осевом направлениях цилиндрической системы координат.

Из практических методов определения остаточных напряжений по толщине поверхностного слоя наиболее точными являются механические методы [3, 4], при которых из исследуемой детали вырезаются образцы в виде полосок, колец, пластинок и другой формы. Далее производится измерение деформаций при удалении поверхностных слоёв с остаточными напряжениями. Для перехода от деформаций, измеренных при удалении слоёв образца, к зависимости остаточных напряжений по толщине поверхностного слоя применяются методики, основанные на известных решениях теории упругости для стержней, пластинок, колец.

Для контроля качества упрочнения деталей методами поверхностного пластического деформирования, но с сохранением исследуемой детали, на практике применяется аналогичные методики с удалением упрочнённого поверхностного слоя на пластинках и кольцах, вырезанных из образцов-свидетелей. Образцы-свидетели проходят технологический процесс упрочнения вместе с обрабатываемой деталью. Следует отметить, что, однако, этот способ контроля качества упрочнения является приближённым, так как реальная деталь имеет сложную форму и в местах концентрации наблюдается значительное перераспределение остаточных напряжений, а для количественной оценки влияния упрочнения на характеристики сопротивления усталости необходимо знать достаточно точное распределение остаточных напряжений в поверхностном слое опасного сечения детали [3–6].

Применение метода термоупругости с использованием конечно-элементного моделирования и расчётных комплексов типа PATRAN/ NASTRAN позволяет значительно расширить возможности исследования и практического определения распределения остаточных напряжений в деталях сложной геометрической формы, подвергаемых методам поверхностного пластического деформирования (ППД) совместно с образцами-свидетелями.

Предлагаемый метод исследования основан на известном в теории и практике механики остаточных напряжений положения о том, что обрабатываемые методами ППД деталь и образец-свидетель простой формы, имеющий по отношению к детали определённые соотношения геометрических размеров [7], получают одинаковые первоначальные деформации [8].

Если обозначить, пропорциональную первоначальным деформациям, матрицу деформаций через {Sg}, то напряжения {^} в соответствии с законом Гука

■ {а} = М({£}-{£0}), (9) где [D] – матрица упругости, содержащая характеристики материала,

{g} – матрица полной деформации,

М^Г = [»_г,а₂,стд,т_г2] ,         (10)

	1	д	д	0
		1-д	1-д
	Д	1	д	0
Гп1 _  £(1-м)	1-д		1-д
“ (1+д)(1-2д)	д	д	1	(11)
	1-д	1-д
	0	0	0	1-2д
				2(1-^J

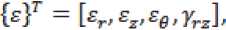
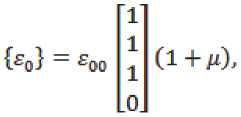
где £  – величина изотропной первоначальной деформации.

Связь между деформациями и перемещениями в этом случае имеет следующий вид:

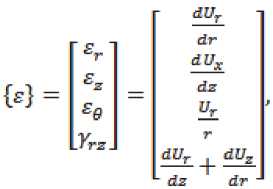
где и – радиальные перемещения, и – осевые перемещения, т – радиус цилиндра.

Если в качестве первоначальных рассматривать температурные деформации, то

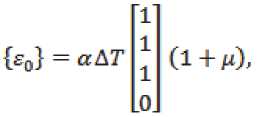
где tz – температурный коэффициент линейного расширения, AT – разность температур.

Из уравнения (9) видно, что при одинаковой первоначальной деформации деталь и образец-свидетель будут иметь различные собственные поля напряжений, так как имеют разные матрицы жёсткости. Для подтверждения этого утверждения к имеющемуся численному расчёту цилиндра (рис. 1) с b = 5 мм (R5) дополнительно были выполнены расчёты для b = 7,5 мм (R7,5) и b = 10 мм (R10) с одинаковыми значениями остальных параметров. Результаты расчётов распределения остаточных напряжений представлены на рис. 5 – 7. На графиках отсчёт оси y выполнялся от поверхности к оси цилиндра (рис. 1).

Из приведённых на рис. 5–7 данных видно, что с увеличением диметра цилиндра растёт величина сжимающих остаточных напряжений в поверхностном слое при одной и той же первоначальной деформации. Величина же растягивающих остаточных напряжений в сердцевине цилиндра (реактивных) с увеличением жёсткости, наоборот, падает. Установленная в настоящем исследовании расчётным путём закономерность наблюдалась при экспериментальном определении остаточных

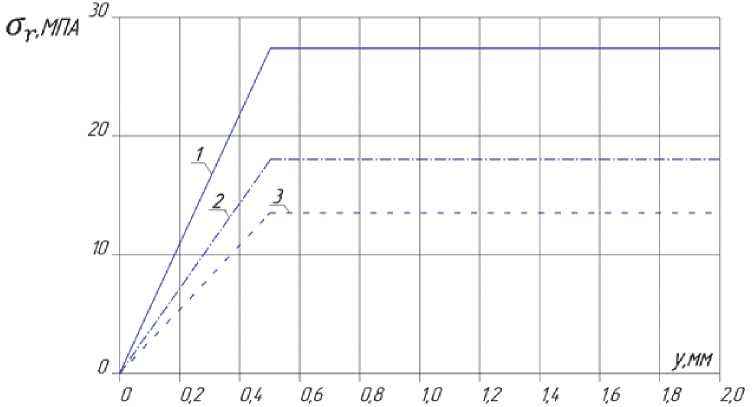
Рис. 5. Распределение радиальных £7 остаточных напряжений по сечению цилиндра: 1 – R5, 2 – R7.5, 3 – R10

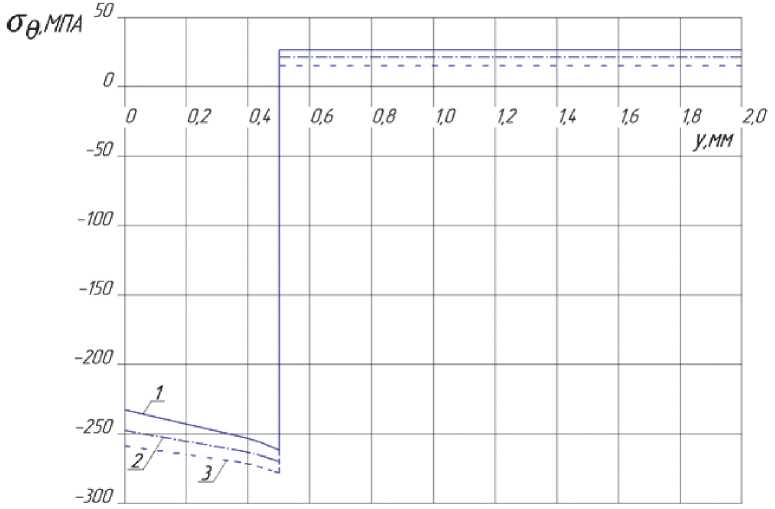
Рис. 6. Распределение окружных tJg остаточных напряжений по сечению цилиндра: 1 – R5, 2 – R7.5, 3 – R10

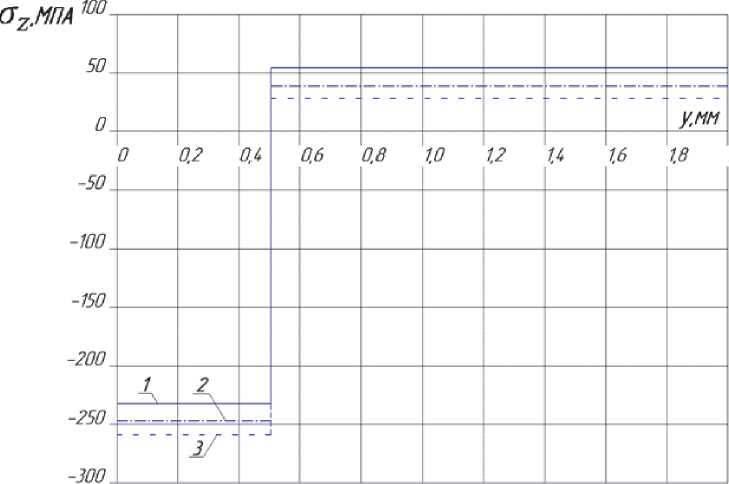
Рис. 7. Распределение осевых tJ остаточных напряжений по сечению цилиндра: 1 – R5, 2 – R7.5, 3 – R10

напряжений в цилиндрических образцах диаметром 10 – 50 мм из стали 45 и сплава Д16Т после гидродробеструйной обработки [4].

На основании изложенного выше предлагается следующий порядок определения распределений остаточных напряжений в поверхностно упрочнённой детали по результатам исследования образца-свидетеля, обработанного одновременно с деталью:

– определение распределения остаточных напряжений по толщине упрочнённого поверхностного слоя образца-свидетеля (например, методом колец и полосок);

– определение на конечно-элементной модели образца-свидетеля первоначальных деформаций в виде температурных зависимостей по направлениям осей системы координат (при установленном экспериментально соотношении между их компонентами для данного технологического процесса упрочнения);

– расчёт распределения остаточных напряжений на конечно-элементной модели детали по полученным первоначальным деформациям (методом термоупругости).

Таким образом, полученные разработанным в настоящем исследовании методом результаты расчётов распределения остаточных напряжений в поверхностно упрочнённой детали позволят в дальнейшем решить следующие важные для практики задачи:

• -    прогнозирование приращения предела выносливости детали за счёт поверхностного упрочнения;

• -    выбор наиболее оптимальных, по сопротивлению усталости, режимов технологического

процесса упрочнения детали.

Решение этих задач приведёт к сокращению длительных и дорогостоящих испытаний деталей машин на усталость.