Применение методики прогнозирования масштабируемости для построения систем высокой доступности на основе СУБД ORACLE

В современном мире, в котором количество информации и количество пользователей постоянно растет, становятся актуальными вопросы прогнозирования возможностей масштабирования информационных систем (то есть увеличения нагрузки на систему без потери производительности). Особенно остро этот вопрос стоит для систем, к которым предъявляются повышенные требования по высокой доступности. Современные информационные системы невозможно представить без СУБД, которые входят в их состав, отвечают за оперативное хранение и обработку данных и часто оказываются узким местом в обработке запросов пользователей.

Наличие математической модели, описывающей поведение вычислительного комплекса при увеличении нагрузки, позволяет делать обоснованные выводы сразу по нескольким вопросам. Каково возможное увеличение среднего количества пользователей, обслуживаемого данной системой? Выдержит ли система предполагаемый пик нагрузок? Какая из подсистем требует наиболее скорого обновления оборудования?

При рассмотрении последнего вопроса речь идет о таких подсистемах, как вычислительная подсистема, связанная непосредственно с работой процессоров (CPU), а также подсистема ввода/ вывода, куда можно отнести работу с системами хранения данных, сетевыми интерфейсами и т. д.

В первой части статьи приводятся понятия теории массового обслуживания, рассматриваются основные параметры производительности информационной системы, устанавливаются их взаимосвязи.

Во второй части приводится сравнение теоретических результатов и результатов тестов на малых (размером менее 100 Гб) базах данных на различном оборудовании.

В третьей части работы рассматривается построение прогноза для реальной промышленной системы с объемом файлов данных более 2 Тб.

Построение математической модели транзакционного процессора СУБД

Под транзакционным процессором будем понимать основной элемент вычислительной системы, отвечающий за выполнение запроса пользователя. В рамках транзакционного процессора можно выделить две составляющие: блок CPU, отвечающий за вычисления, и блок I/O, отвечающий за ввод/вывод (рис. 1).

Обслуживание на CPU принципиально отличается от обслуживания I/O: особенностью всех операционных систем является единая очередь для всех процессоров, в то время как устройства ввода/вывода могут иметь несколько очередей, создаваемых с помощью различных контроллеров ( рис. 2 ).

При малой нагрузке на сервер на выполнение каждой транзакции затрачивается ровно столько времени, сколько требуется для проведения операций транзакционного процессора. Однако при большом числе транзакций, когда время выполнения каждой транзакции становится выше, чем интервал поступления новых клиентских запросов, начинает создаваться очередь.

Таким образом, время выполнения транзакции (response time) можно вычислить как:

R t = S t + Q t , (1)

где S_t – время обслуживания (service time); Q_t (queue time) – время ожидания в очереди.

Будем рассматривать простейший (пуассоновский) поток транзакций (заявок), у которого интервалы между моментами поступления транзакций распределены по экспоненциальному закону с параметром λ . λ является средним числом заявок, поступающих в единицу времени, и характеризует интенсивность входящего потока. Средняя продолжительность обслуживания одной заявки является случайной величиной Т , измеряемой в единицах времени. Произведение величин A = λТ показывает величину нагрузки на систему.

Вероятность поступления k заявок за время t подчиняется распределению Пуассона и описывается формулой [1]:

Рис. 1. Составляющие транзакционного процессора

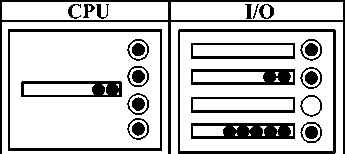
Очередь процессора Очереди ввода/вывода

Рис. 2. Основные отличия очередей CPU и I/O

p k

( 2 tL , » k !

При этом среднее число заявок в интервале t : k = λt .

Заявки могут сбрасываться, т.е. аннулироваться (система с отказами), или становиться в очередь и ждать освобождения ресурсов неопределенно долгое время, после чего обслуживаться в течение необходимого интервала времени (система с ожиданием), возможны промежуточные случаи, например, модели с ожиданием, но в течение ограниченных интервалов времени. Рассмотрим системы с ожиданием. Для них вероятность того, что поступивший вызов не обслуживается немедленно, а становиться в очередь описывается следующим выражением (формула Эрланга-С) [2]:

ANN

p = p0 N!(N - A) ’ p0 = N-1 An    ANN

+ —7---A

Z0> n ! N ! ( N - A )

,

где N – число каналов обслуживания; А – нагрузка на систему; p₀ – вероятность того, что все каналы свободны.

Преобразуем данную формулу к более удобному виду:

p =            N - 1    "

N!(N - A )£ AX I + ANN n = 0

и разделим числитель и знаменатель на N!N :

A

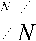
p =

,             . N - 1       ,        „ ,

A An    AN n=0

. (2)

Поскольку СУБД является системой с очередями (то есть с ожиданием), то для описания ее работы предлагается использовать именно эту формулу.

Непосредственный расчет по формуле (2) может быть достаточно трудоемким, поэтому в качестве варианта быстрого вычисления значений предлагается использовать алгоритм Ягермана [3].

Запишем формулу (2) в терминах СУБД [4]. Обозначим через λ_sys общий транзакционный поток в системе (число транзакций в единицу времени), λ_q – поток на одну очередь, Q_n – число очередей в системе. В этом случае λ q = λ sys /Q n . Формула (2) (формула Эр-ланга-С) в терминах СУБД будет иметь вид:

E c ( m , S t , X q ) =

(mSAq)

-_________________ m !

( i - ms , ^ m - i V mS xqNL ₊N S NN 1N0     k !          m !

где m – число транзакционных процессоров для очереди, S_t – время обслуживания.

Введем понятие утилизации U = S_tλ_q /m [4]. Тогда время ожидания в очереди можно выразить как

Q = E c S t— ,

Vt m (1 - U)

а длина очереди Q тогда представима как Q = λ_qQ_t .

Cравнение теоретических зависимостей и экспериментальных результатов

Рассмотрим, применима ли эта математическая модель к работе реальных СУБД. Для этого были проведены следующие экспериментальные исследования. Была создана таблица с достаточно большим объемом информации (около 600 Мб), чтобы исключить возможную конкуренцию за доступ к одним и тем же данным, а, следовательно, обеспечить отсутствие внутренних очередей. После этого на базу данных создавалась нагрузка с эмуляцией работы различного числа пользователей. Эта последовательность действий выполнялась на трех различных ЭВМ:

• 1.    AMD Athlon 64 x2 Dual-Core Processor TK-57 1.9GHz;

• 2.    Intel Core2Duo T7300 2GHz;

• 3.    AMD Athlon II x4 640 Quad-Core Processor 3.0GHz.

Результаты экспериментов приведены на рис. 3 .

Оценка результатов даже этого простого теста позволяет сделать выводы о резком возрастании времени обработки запроса после превышения порога в 35 транз/с и 60 транз/с для Athlon x2 и Intel Core2Duo соответственно. В то же время Athlon x4 показывает удовлетворительные результаты даже при потоке 240 транз/с. Знание этих границ позволит заранее предсказать поведение вычислительного комплекса и предпринять необходимые меры в системах, к которым предъявляются повышенные требования по высокой доступности.

Более подробно рассмотрим платформу AMD Athlon II x4 и сравним результаты экспериментов с расчетами, получаемыми по формуле (3). Эта теоретическая формула позволяет предсказывать поведение для систем с различным числом процессоров. Возьмем для расчетов формулу (3) с параметрами m = 3 и m = 4 ( рис. 4 ).

Форма полученной экспериментальной зависимости соответствует теоретической, но на графике видно, что аппроксимирующая кривая проходит между кривыми, рассчитанными для значений m = 3 и m = 4 (3 и 4 процессора). Полученное в эксперименте промежуточное значение можно определить как число эффективных процессоров (процессоров, непосредственно занятых обработкой запросов пользователей). Отличие этого числа от физического максимума объясняется работой операционной системы и дополнительных приложений, однако с ростом нагрузки число эффективных задействованных процессоров стремится к максимуму. О вычислении количества эффективных процессоров будет рассказано далее.

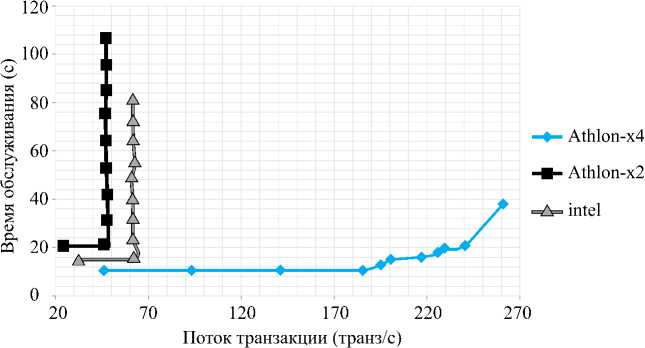
Рис. 3. Результаты процессорного теста на различных ЭВМ

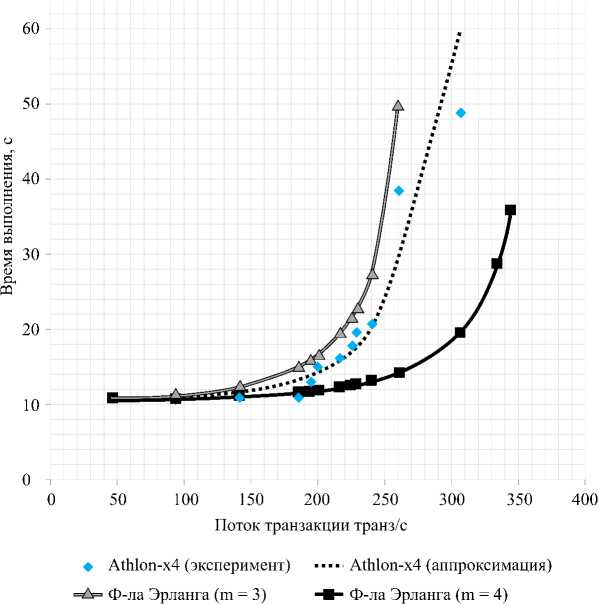
Рис. 4. Сравнение теоретических расчетов и результатов экспериментов

Построение прогноза для больших баз данных

Уравнение времени обработки для выбранного статистического показателя нагрузки можно записать в следующем виде [4]:

R t = S t /(1 – U^M)                 (4)

– для процессорной подсистемы и

R t = S t /(1 – U) (5)

– для подсистемы ввода/вывода, где M – число эффективных процессоров, R_t – полное время обработки для данного вида нагрузки, S_t – время обработки на процессоре, U – утилизация подсистемы.

Это уравнение можно преобразовать, умножив обе части уравнения на величину транзакционного потока λ , получатся выражения:

λR t = λS t /(1 – U^M) и

λR t = λS t /(1 – U) .

Заметим, что λR_t = R – общее время обработки нагрузки БД, а λS_t = S – общее процессорное время, затраченное БД. Получаем:

R = S /(1 – U^M) и

R = S /(1 – U) .

специальных таблицах и использовать

их для расчета числа эффективных про-

цессоров по формуле (6). После определения значения M можно построить зависимость времени обработки по формуле (для процессорной подсистемы):

R t =

1 -

Формула (4) в данном случае принима-

ет следующий вид:

R =

1 -

S t

M

S t

0, 04147

M

_-

0,04147 • X

75, 63271

75,63271

Для вычисления количества эффективных процессоров необходимо решить уравнение

R t – S t /(1 – U^M) = 0 .

Для упрощения процесса решения его можно преобразовать к следующему виду

^

^{S t λ} M

M

^S t     0 .

R t

Данное уравнение можно решить чис- ленно.

Средства администрирования СУБД Oracle (репозиторий снимков состояния системы) позволяют измерить значения статистических показателей ( session logical reads, user calls, physical read total IO requests, physical write total IO requests, redo writes ), сохранить их в

Рассмотрим пример из практики. На вычислительном комплексе, содержащем 128 процессоров и обрабатывающем БД размером более 2 Тб, с помощью средств администрирования были измерены значения статистических показателей (St, Qt, Rt, λ) для процессорной подсистемы (CPU) и подсистемы ввода/вывода (I/O) (табл. 1). На основе этих данных было рассчитано значение М (число эффективных процессоров). Проведем анализ работы процессорной подсистемы и подсистемы ввода/выво-да. Для примера возьмем точку № 14. В ней были получены следующие значения показателей для процессорной подсистемы: λ = 1793,369 – величина транзакционного потока (транз/мс); St = 0,04147 – время обслуживания на процессоре (мс); M = 75,63271 – число задействованных эффективных процессоров.

График зависимости времени обработки ( R_t ) от величины транзакционного потока ( λ ) приведен на рис. 5 .

Таким образом, можно сделать вывод, что для 76 процессоров предельная нагрузка достигается при λ = 1800 транз/мс. При более высоких значениях время обработки резко возра- стает.

В точке № 14 также были получены значения показателей для подсистемы ввода/вывода: λ = 8.98787 – величина транзакционного потока (чтений/мс); S_t = 8.27529 – время обслуживания на процессоре (мс); M = 263.793 – число задействованных эффективных процессоров.

Формула (5) в данном случае принимает вид:

S_t        8, 27529

5X ~ 1 _ 8,27529■ X

M 263,793

Таблица 1. Выборка данных, полученная на промышленной системе

№	CPU					IO
	St , мс	Qt , мс	Rt , мс	λ , транз/мс	M	St , мс	Qt , мс	Rt , мс	λ , чтен./мс	M
1	0,061	0,057	0,118	1748,17	106,6	5,940	5,591	11,531	17,82	218,3
2	0,053	0,040	0,093	1675,45	89,1	5,591	4,284	9,876	15,79	203,5
3	0,069	0,050	0,120	1683,28	117,4	6,816	4,961	11,777	17,10	276,7
4	0,057	0,039	0,097	1758,65	101,8	6,644	4,566	11,210	15,19	247,8
5	0,057	0,044	0,101	1651,76	94,5	6,205	4,809	11,014	15,09	214,5
6	0,063	0,040	0,103	1762,80	111,6	7,799	4,940	12,740	14,19	285,3
7	0,050	0,036	0,086	1661,45	84,5	6,174	4,408	10,582	13,55	200,8
8	0,047	0,034	0,082	1672,03	80,2	5,727	4,146	9,873	13,85	188,9
9	0,045	0,030	0,075	1278,13	58,8	5,723	3,785	9,507	10,12	145,4
10	0,044	0,035	0,079	1450,81	64,1	5,395	4,317	9,712	11,74	142,5
11	0,045	0,031	0,075	1534,68	69,2	5,653	3,897	9,550	12,09	167,4
12	0,042	0,027	0,069	1674,51	71,7	6,034	3,831	9,865	11,72	182,1
13	0,042	0,018	0,060	1851,04	79,0	8,340	3,500	11,841	9,32	263,0
14	0,041	0,016	0,058	1793,37	75,6	8,275	3,249	11,525	8,99	263,8
15	0,038	0,015	0,053	1702,55	66,7	8,321	3,248	11,569	7,87	233,2
16	0,036	0,013	0,050	1489,50	55,4	7,935	2,904	10,839	6,82	202,0
17	0,036	0,014	0,050	1178,48	43,1	7,286	2,903	10,189	5,75	146,9
18	0,034	0,020	0,054	891,26	31,4	6,643	3,949	10,591	4,58	81,6

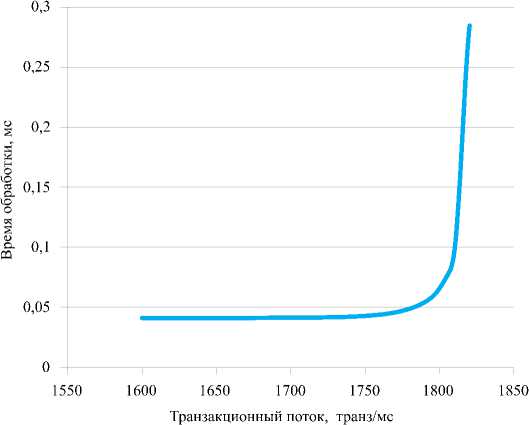
Рис. 5. Зависимость времени обработки от величины транзакционного потока (процессорная подсистема)

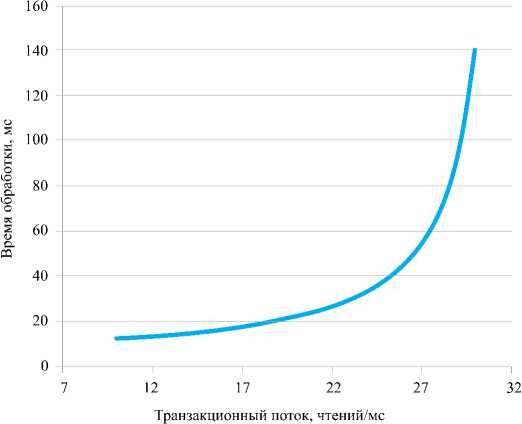
Рис. 6. Зависимость времени обработки от величины транзакционного потока (подсистема ввода/вывода)

График зависимости времени обработки ( R_t ) от величины транзакционного потока ( λ ) приведен на рис. 6 .

На графике видно, что при λ > 25 чте-ний/мс подсистема ввода/вывода уже не сможет эффективно обрабатывать нагрузку.

Таким образом, для реально работающих систем можно предложить следующую методику прогнозирования увеличения на них нагрузки.

• 1.    Провести измерения значений статистических показателей (с помощью средств администрирования СУБД Oracle).

• 2.    Провести расчеты количества эффективных процессоров согласно формуле (6).

• 3.    Составить общую таблицу измеренных и рассчитанных значений (по аналогии с табл. 1 ).

• 4.    Выбрать в таблице характерные точки (с достаточной нагрузкой СУБД) и для них построить зависимости времени обработки от величины транзакционного потока для процессорной подсистемы и подсистемы ввода/вывода.

• 5.    Провести анализ полученных зависимостей для определения пороговых значений транзакционного потока, выше которых время обработки резко возрастает.

• 6.    Полученные пороговые значения позволят сделать обоснованный вывод, например, о наличии или от-

• сутствии необходимых резервов для увеличения количества обрабатываемых заявок.

Заключение

В результате можно сделать вывод о применимости теории массового обслуживания для построения математической модели, описывающей поведение СУБД при увеличении нагрузки. В качестве математической модели рассмотрена модель Эрланга-С (система массового обслуживания с очередями) в нотации статистик СУБД Oracle. Предложенные в статье зависимости подтверждаются на практике результатами экспериментов с небольшими базами данных (размером менее 100 Гб) на различных аппаратных платформах, а также результатами измерений на реально работающей системе с объемом данных более 2 Тб.