Применение методов дискретной математики при модульном синтезе мехатронных устройств

При разработке технических систем [1] прибегают к двум способам их описания: структурному (анализ внутреннего устройства) и функциональному (анализ взаимоотношений со средой и между частями (модулями) системы).

Функциональная структура системы является всеобъемлющей, так как именно функциональные компоненты и их синергетическое объединение в одном объекте [2] являются основой структурного описания объекта. В данном случае мехатронной манипуляционной системы (ММС) эти компоненты в ММС собраны в изделии по принципу модульного проектирования.

При расчете параметров различных технических систем эффективны топологические методы анализа, основанные на теории графов, вычислении структурных чисел и т.д. и представляющие собой методы решения задач так называемой комбинаторной (дискретной) математики [3]. Эти методы применимы для компьютерного анализа и синтеза допускают системный подход.

Принципиальным преимуществом задач в дискретной математике является то, что большинство задач решается перебором (организованным и неорганизованным).

Теория графов является одним из разделов дискретной математики и строится на основе общих понятий теории множеств, тесно связана с ними. В данной статье основное внимание уделяется практическим приложениям в мехатронике.

Достоинством теории графов является наглядность, гибкость, что позволяет учитывать связи модулей рассматриваемой технической системы, определять воздействия управляющих сил и моментов, оценивать влияние отдельных модулей на другие в любой точке системы. Преимущества применения теории графов проявляются тем существеннее, чем сложнее исследуемая система.

С точки зрения понятий теории множеств можно ассоциировать два множества: множество V = { v 1 , ^ , v n } объектов v i называемых вершинами, связи между которыми определены множеством ребер E = { e 1 ,e ₂,... e m } . Их называют графом и обозначают о = ( V , E ) . Эти объекты изображают в виде диаграмм на плоскости кружками (вершины), а связи между ними - линиями (ребра). Элементы множества E ребер связывают пары элементов множества вершин V , т.е. одна пара вершин определяет одно ребро, являясь его границами, или можно сказать, что ребра изображают бинарные отношения или соответствия вершин графа. Расширение возможностей отображения свойств связей между объектами с помощью графов состоит в приписывании ребрам некоторых количественных показателей, называемых весами.

Графы особенно необходимы при представлении компоновочных структур сложных многозвенных механизмов (рис. 1, б). Граф напоминает упрощенную кинематическую схему шарнирно-рычажного механизма многозвенного манипулятора последовательной структуры (рис. 1, а).

Здесь необходимо только выделение неподвижного основания. Вершинами изображаются узлы, реализующие вращательные одноподвижные кинематические пары вместе с приводами (за исключением нулевого, которое соответствует неподвижному основанию), ребрами - звенья, цифрами - кинематические пары.

В работе [4] на основании теории графов исследована кинематическая структура исполнительных механизмов с тросовыми тягами и установлено соответствие между механизмом и его графом. Показано, что структура кинематических цепей с тросовыми тягами аналогична кинематической структуре планетарно-зубчатого механизма. Поэтому уравнение базовой кинематической цепи для кинематического анализа планетарных зубчатых передач можно применять к механизмам с тросовыми тягами и к зубчато-рычажным механизмам. Суть применяемого подхода состоит не в рассмотрении каждого конкретного механизма, а в планомерной процедуре анализа механизмов подобного класса на основании их разбиения на элементарные механизмы (ЭМ) с последующим математическим отождествлением и построением общей процедуры вычислений.

■О о

a)

б)

Рисунок 1 - Кинематическая схема разомкнутой кинематической цепи механизма (а) и её граф (б)

Здесь реализуется именно системный подход, связанный с разбиением системы на элементы, математическим описанием отдельных элементов и объединением этих описаний в единую систему посредством связей.

Топологические методы расчета при синтезе зубчатых механизмов на основе единого подхода, связанного с представлением графа отдельных характеристик механизмов, приве- дены в работе [5]. Здесь в качестве ЭМ, на которые разбиваются сложные зубчатые механизмы, принят трехзвенный планетарный механизм (дифференциал). Для анализа сложных (составных) механизмов при автоматизации процесса вычислений (угловых скоростей звеньев составного механизма, их взаимного положения, моментов и других параметров) удобен матрично-кодовый метод (МКМ) [5,6].

В статье проиллюстрирована возможность применения топологических методов (матрично-кодового, теории графов) к расчету исполнительных механизмов быстродействующих циклоидальных манипуляторов (БЦМ) [6,7], которые являются составными, из них можно выделить отдельные ЭМ и математически описать.

Особенностью БЦМ является то, что их реализация является одним из способов решения фундаментальной проблемы мехатроники (робототехники) – проблемы быстродействия промышленных роботов (ПР).

Для обычных ПР с независимыми приводами по степеням подвижности требуемые движения реализуются при последовательном включении приводов (на каждом этапе работает только один привод, в ту или другую сторону). В начале каждого этапа привод должен разгонять подвижную часть, в конце – тормозить.

Таким образом, актуальной является задача реализации определенного типа движения рабочего органа и соответствующего выбора компоновочной структуры, а также способа управления ПР [7].

Быстродействие манипулятора можно получить за счет геометрии движений, обеспечивая при этом требуемую точность получаемых траекторий.

В основу быстродействующих циклоидальных мехатронных устройств заложена идея, заключающаяся в том, чтобы задавать требуемую траекторию и закон движения рабочего органа кинематическими средствами (выбором кинематический схемы), а привод осуществлять от постоянно вращающегося двигателя [7] и получить повышенное быстродействие.

Ниже представлена классификация возможных компоновочных структур и способов реализации управления ММС. В частности, в случае использования одного привода возможны компоновки с зубчатой, планетарной, цепной, с тросовыми тягами передачей.

Виды кинематических пар		Кинематика руки
Смешанные		С размыканием кинематической пары
Полусмешанные		Многорукие
Вращательные		С выдвижением
		С вращением

Число и расположение приводов		Виды передач
Несколько по степеням подвижности		С тросовыми тягами
Один		Зубчатые

Планетарные Цепные Прямые

Система синхронизации		Устройство управления
Электронная		Электронноадаптивное
Механическая		Электронноцикловое
		Механическое

Рисунок 2 – Классификация компоновочных структур ММС

В соответствии с конкретными топологическими требованиями из определенного набора модулей можно сформировать простые быстродействующие манипуляторы с высокими функциональными свойствами. Примером может служить двухцепной зубчато-рычажный циклоидальный манипулятор, представленный на рисунке 3.

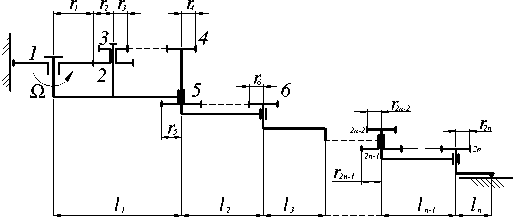
Ω - угловая скорость вращения приводного двигателя Рисунок 3 – Схема n-цепного зубчато-рычажного манипулятора

Для иллюстрации методики модульного проектирования рассмотрим частный случай трехцепного механизма (А.С. СССР №1266759 БИ. 1986. П40) рис. 4.

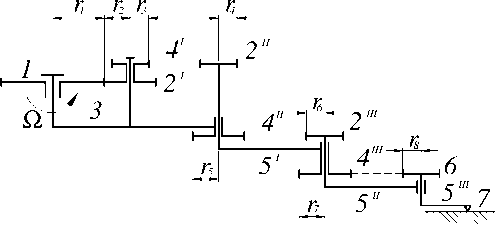
Рисунок 4 – Кинематическая схема трехцепного циклоидального манипулятора

Будем использовать иерархическую систему модульного проектирования ММС, позволяющую генерировать модули каждого уровня из модулей более низкого уровня. Для этого зададим ряд исходных базовых модулей согласно таблице 1.

Таблица 1

№ п/п	Базовый модуль
	Условное обозначение		Наименование
1			Неподвижное зубчатое колесо
2	,		Корончатое колесо
3			Водило
4	—		Цепная передача
5		-------------------------------------II	Соединительное звено
6			Зубчатое колесо
7			Рабочий орган (схват)

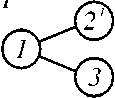
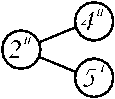
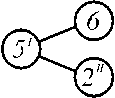
Тогда в соответствии с кинематической схемой можно составить возможные комбинации модулей соединения ЭМ, представленный на рисунке 5. Из базовых модулей с учетом их взаимосвязи можно получать ЭМ.

V

IX

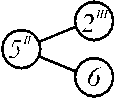
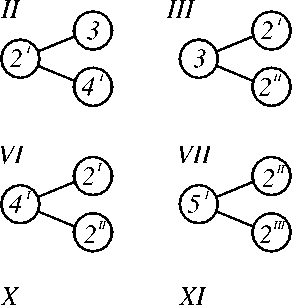
Рисунок 5 – Модули соединения ЭМ

IV

VIII

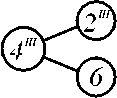
Совокупность полученных модулей соединения, из которых вытекает модель всей компоновочной структуры, можно представить в виде графа рисунок 6.

Таким образом, иерархическая система модульного синтеза состоит из уровней: нижнего – соответствует набору исходных базовых модулей; среднего – модули соединения со связью ЭМ; верхнего – структурная модель манипулятора (компоновочная структура).

Рисунок 6 – Граф модели компоновочной структуры

Совокупность модулей соединения ЭМ в виде графов и графа модели компоновочной структуры можно представить также как матрицу смежности, отражающую связь вершины 1 и вершины 5II или 7 смотри таблицу 2, в которой рассматривается множество вершин.

Таблица 2

Начальная вершина	Конечная вершина
	1	2 I	2 II	3	4 I	4 II	5 I	5 II	6	7
1	1	1	0	1	0	0	0	0	0	0
2I	1	1	0	1	1	0	0	0	0	0
2 II	0	0	1	1	1	1	1	0	0	0
3	1	1	1	1	0	0	0	0	0	0
4 I	0	1	1	0	1	0	0	0	0	0
4 II	0	0	1	0	0	1	0	0	1	0
5 I	0	0	1	0	0	0	1	0	1	0
5 II	0	0	0	0	0	0	0	1	1	1
6	0	0	0	0	1	1	1	1	1	0
7	0	0	0	0	0	0	0	1	0	1

Ячейки со значением 1 указывают на то, что возможна генерация только одной комбинации компоновочной структуры и, очевидно, далее возможно обобщение на случай n – цепного механизма.

Таким образом, наиболее просто ММС можно реализовать посредством подобных устройств с полициклоидальными траекториями рабочих органов [6, 7], где имеются один привод с использованием планетарно-зубчатых, зубчато-рычажных механизмов и меха- низмов с тросовыми тягами. Для синтеза требуемых значений параметров, характеризующих отношение угловых скоростей вращения ведомых звеньев и ведущего звена, применимы топологические методы – матрично-кодовый метод и метод графов [3].

В работе [6] приведен топологический расчет для общего случая цепного зубчаторычажного механизма (рис. 3) матрично-кодовым методом. Для расчета необходимо разбить составной механизм на ЭМ и составить кинематические уравнения. Алгоритм расчета приведен на рисунке 7.

Рисунок 7 – Алгоритм расчета быстродействующего циклоидального манипулятора на основе матрично-кодового метода

В этом механизме используются три типа двухзвенных ЭМ (каждый ЭМ представляет собой пару зубчатых колес):

тип муфты (т.е. два колеса, насаженных жестко на одну ось);

два колеса, охваченных цепной передачей;

сателлиты на водиле Ω ( r ₁ + r ₂ ) = ω ₂ r ₂ .

Уравнения взаимосвязи для каждого ЭМ будут ( Ω - угловая скорость водила):

связь (1, 2): Ω ( r ₁ + r ₂ ) = ω ₂ r ₂ ;

связь (2, 3): ω ₂ = ω ₃ ;

связь (3, 4): ω ₃ r ₃ = ω ₄ r ₄ ;

связь (4, 5): ω ₄ = ω ₅ ;

связь (5, 6): ω ₅ r ₅ = ω ₆ r ₆ ;

связь (2 n - 2,2 n - 1) : ω _{2 n - 1} r _{2 n - 1} = ω _{2 n - 2} r _{2 n - 1} ;

связь (2 n - 1, 2 n ) : ω _{2 n - 1} r _{2 n - 1} = ω _{2 n - 2} r _{2 n - 1} .

Из этих уравнений формируется производящая матрица [5, 6] размерностью 2 n × 2 n :

	r l + r 2	- r 2	0	0…	0	0	0
	0	1	- 1	0…	0	0	0
	0	0	r 3	- r 4     …	0	0	0
Ω ω 2 … ω 2 n - 1 ω 2 n =	• : 0	0	0	0…	- r 2 n - 2	0	0
	0	0	0	0…	1	- 1	0
	_ 0	0	0	0…	0	r 2 n - 1	- r 2 n

ω откуда вычисляются передаточные числа Ni = Ωi+1 ,i = 1,2,…,n .

В частности, имеем:

_{N =} ω _{2 n =} det Ω ω 1 ω 2 ⋯ ω 2 n - 1 ^{2 n - 1}    Ω    det ω 1 ω 2 ⋯ ω 2 n - 1 ω 2 n

= ( r ₁ + r ₂ ) r ₂ ^{- 1} r ₃ r ₄ ^{- 1} … r _{2 n - 1} r ₂ ^- _n ¹ , (*)

т.е. передаточные числа N _i определяются структурными вычислениями. Алгоритм вычислений приведен на рисунке 10.

Вычисления можно осуществить и на основе преобразований графа механизма (рис. 11), где вершины соответствуют зубчатым колесам, а ребра – связям, штриховой линией обозначены цепи, соединяющие колеса. На графе указаны веса, которые вычисляются:

для ребра (1, 2) существует связь между водилом и сателлитом ( Q ( r 1 + r ₂ ) = to ₂r ₂ ) ;

для ребра (2, 3) - между колесами 2 и 3 ( to₂ = < У ₃ ) ;

для ребра (3, 4) - через цепную передачу ( to ₃r₃ = < У ₄ r ₄ ) и т.д.

После преобразования данного линейного графа нетрудно убедиться в том, что для любой вращательной пары и всего механизма формула (*) для чисел N _i совпадает.

Последовательность расчетов в задаче анализа следующая:

исходя из структуры механизма устанавливается множество ЭМ, составляющих исходный механизм и их функциональные зависимости;

для каждого режима строится матрица режима;

вычисляются выходные характеристики (в частности для зубчато-рычажной компоновки – передаточные числа на режимах);

определяются параметры исполнительного механизма (скорости, ускорения, моменты и т.д.).

При решении задачи синтеза последовательность следующая:

с помощью специального алгоритма порождается некоторое множество ЭМ (обычно множество ограничивается его мощностью и классом используемых ЭМ);

строится структура механизма из порожденного множества ЭМ;

решается задача анализа;

процесс порождения различных исходных множеств ЭМ продолжается до тех пор, пока не будут выполнены технические условия на синтез.

Компоновочные структуры БЦМ имеют отображение в виде линейного графа и передаточные числа N _i вычисляются перемножением весов ЭМ.

На основе преобразования графа можно (не вычисляя) непосредственно определить значение N _i . Обобщим результаты для n -цепного БЦМ в зубчато-рычажной компоновке рисунок 8.

Компоновочные структуры БЦМ имеют отображение в виде линейного графа и передаточные числа N _i вычисляются преумножением весов ЭМ.

r 1+ r 2               r 3                 r 5                        r 2n-1

r2      1      r4      1      r6              1      r2n1    2   3    4    5   6 2n-2 2n-1 2n

вершины графа соответствуют колесам;

пунктиром обозначены цепи, соединяющие колесо;

веса ребер графа указаны возле них.

Рисунок 8 – Граф механизма с указанием весов ребер

Таким образом, применение методов дискретной математики при расчете параметров компоновочных структур БЦМ наглядно и эффективно.