Применение методов фрактального анализа при исследовании механизмов деформирования и разрушения образцов эпоксидных полимеров под действием растягивающих напряжений

Анализ механизмов деформирования и разрушения композиционных строительных материалов является важной задачей строительного материаловедения, актуальность решения которой в связи с разработкой новых видов композиционных материалов на основе полимерных связующих растет год от года. Известно, что разрушение композиционных строительных материалов представляет собой процесс множественного зарождения, развития и агрегации различного рода дефектов и микротрещин вплоть до появления макротрещин [1]. Неоднородность структуры строительных материалов приводит к формированию ослабленных зон, с которых впоследствии и начинается разрыхление и разрушение композитов. Достижение микротрещиной включения (поры или заполнителя) приводит к сбросу критической плотности энергии в устье трещины и переходу системы к нестабильному состоянию (точке бифуркации). В точке бифуркации возможно ветвление, изменение механизма и направления развития трещины разрушения [2]. При этом разрушение имеет вероятностную природу, а сам процесс накопления повреждений самоподобен, что делает перспективным использование для его анализа методов фрактального анализа [2–5].

В научной литературе приводятся различные способы определения фрактальной размерности структуры реальных композиционных материалов на основе цементных вяжущих и полимерных связующих [1; 5–10]. В работах [11; 12] авторским коллективом предложена методика определения фрактальной размерности кривых деформирования на основе метода минимального покрытия, позволяющая получать интегральную количественную оценку процесса разрушения мелкозернистых бетонов при сжатии и определять положение параметрических точек кривой разрушения, построенной с высокой частотой снятия показаний (0,01 сек.). Последующее использование предложенной методики при анализе кривых деформирования образцов мелкозернистых бетонов с различными комплексами модифицирующих добавок показал его перспективность для получения ценной информации о процессе разрушения композиционных материалов различной природы. В данной работе разработанный подход был использован для фрактального анализа механизма деформирования и разрушения полимерных композиционных материалов под действием растягивающих нагрузок.

В качестве объекта исследования был выбран полимер, получаемый на основе модифицированной эпоксидной смолы Этал-247 (ТУ 2257-247-18826195-07), отверждаемой отвердителем Этал-1440Н (ТУ 2257-3570-18826195-03), представляющим собой смесь ароматических и алифатических ди- или полиаминов, модифицированную салициловой кислотой. Технические характеристики смолы Этал-247: массовая доля эпоксидных групп – не менее 21,4-22,8%; вязкость по Брукфильду при 25 ^о С – 650-750 СПз. Компаунды, отверждаемые Этал-1440Н, имеют длительную жизнеспособность – 4-5 часов при +20°С, обеспечивают теплостойкость отвержденных композиций по Мартенсу до 140°С.

Для проведения механических испытаний составов полимерных композитов на растяжение использовалась разрывная машина серии AGS–X с программным обеспечением

TRAPEZIUM X. Частота фиксации значений напряжений и деформаций составляла 0,01 сек. Испытания проводились в соответствии с ГОСТ 11262-2017 (ISO 527-2:2012) «Пластмассы. Метод испытания на растяжение» при температуре 23±2 ^о С и относительной влажности воздуха 50±5%. Скорость перемещения зажимов испытательной разрывной машины составляла 2 мм/мин. Параллельно испытывали не менее 6 образцов, имеющих форму «восьмерок» (тип 2 согласно ГОСТ 11262-2017).

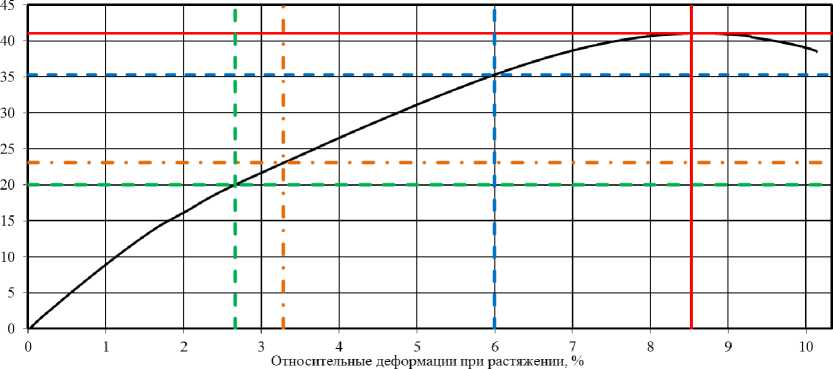
Анализ полученных результатов показал, что кривая деформирования для образцов данного состава характеризуется как восходящей, так и нисходящей ветвями, что позволяет определить прочностные и деформационные характеристики эпоксидного полимера при растяжении и разрыве (рис. 1, а). Предел прочности при растяжении и относительное удлинение при максимальной нагрузке, соответственно, равны 41,05 МПа и 8,53%; предел прочности и относительное удлинение при разрыве (разрушении) – 38,47 МПа и 10,14%.

Детализация кривой деформирования (рис. 1, б), построенной с помощью современного испытательного оборудования с высокой частотой снятия показаний, свидетельствует, что процесс нагружения (рис. 1, а) сопровождается дискретными актами повышения и падения напряжений (рис. 1, б). При этом, учитывая, что изменение деформаций и напряжений в исследуемых образцах при проведении механических испытаний фиксировалось во времени с определенным заданным шагом (0,01 с), для анализа кривых деформирования с выявлением на ней характеристических точек целесообразно применение теории фрактального анализа временных рядов.

Рассмотрим временной ряд y(t), определенный на некотором участке [a, b]. Для вычисления фрактальной размерности используем более точный по сравнению с методом клеточной размерности метод минимального покрытия, основные положения которого изложены в работах [12 – 15]. Суть метода заключается в равномерном разбиении отрезка

wm = [a = to < t1 < ^ < tm = b]

на m частей и подсчете функции y = f(t) в классе покрытий, состоящих из прямоугольников с основанием 6 = b^a (рис. 2 [13]). Тогда высота прямоугольника на отрезке [t i-1 , t i ] будет равна разности между максимальным и минимальным значением функции f(t) на этом отрезке - K i (6). Введя величину амплитудной вариации функции f(t), соответствующей масштабу разбиения 6 на отрезке [a, b]

V f (6) = Z J=i K i (6), (1) получим зависимость для определения полной площади покрытия:

S/6) = Vf(6) x 6. (2)

а)

s с э

максимальное напряжение — “напряжение через 40 с ^^—максимальная деформация — “деформация через 40 с

— — напряжение через 90 с

— “деформация через 90 с

— • критическое напряжение — • критическая де формация

б)

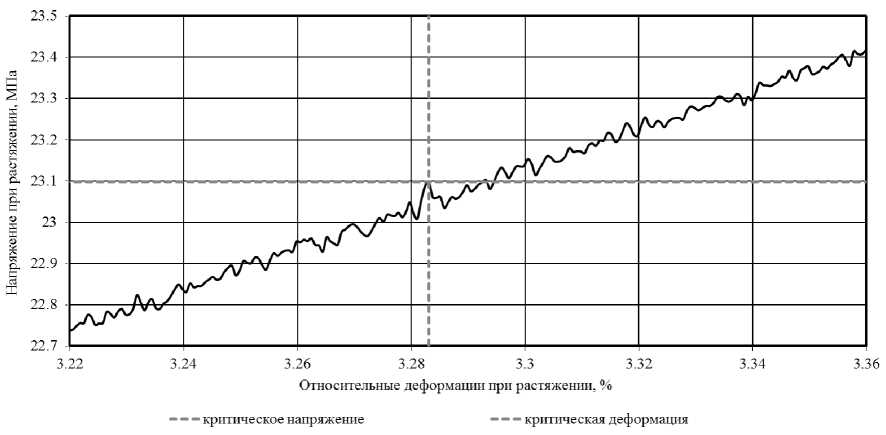
Рис. 1. Общий вид (а) и фрагмент (б) кривой деформирования образцов эпоксидных полимеров при растяжении (сплошной линией красного цвета на рисунке «а» обозначен уровень максимальных напряжений и соответствующих им деформаций).

Тогда согласно [4; 13] индекс фрактальности μ можно определить из линеаризации зависимости

V f (δ)~δ^-μ при δ → 0.                              (3)

При этом фрактальная размерность связана с индексом фрактальности, определяемым методом минимального покрытия, как

D μ = μ+1.                                (4)

Для определения индекса фрактальности μ в данной работе использовалась последовательность m вложенных разбиений, где m = 2n, где n = 0, 1, 2, 3, 4. Каждое разбиение состояло из 2n интервалов, содержащих 24-n экспериментальных точек. Для каждого разбиения ωm вычислялась амплитудная вариация Vf (δ) по формуле (1), где Ki (5) определялась как разница между максимальным и минимальным приростом напряжения при растяжении на временном интервале [ti-1, ti]. По коэффициенту в уравнения регрессии log(Vf(5)) = я0 + в х log (5), определенному с помощью метода наименьших квадратов, определяли индекс фрактальности и размерность минимального покрытия.

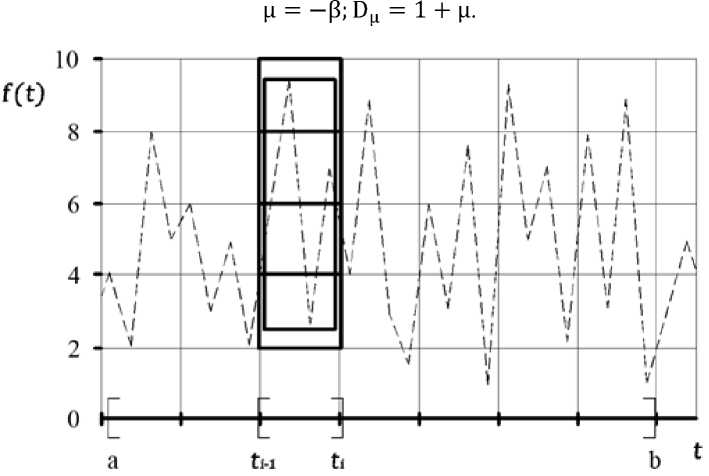
Рис. 2. Фрагмент клеточного (квадраты) и минимального (прямоугольник) покрытий графика фрактальной функции на отрезке [t i-1 , t i ].

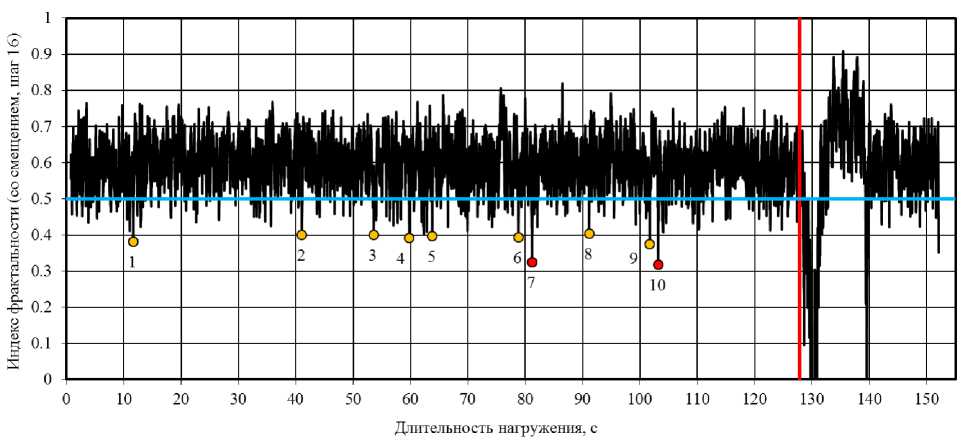
Анализ данных, отражающих изменение индекса фрактальности в зависимости от длительности нагружения, определяемого со смещением анализируемого участка с шагом 24 = 16 точек, показал (рис. 3), что процесс разрушения (правее красной линии) характеризуется резким снижением данного показателя, варьирующегося в процессе нагружения в интервале от 0,33÷0,82, до нулевых значений. При этом из анализа временных рядов известно [11 - 13], что чем выше значение р, тем стабильнее ряд. Если р < 0,5, то ряд интерпретируют как «тренд» (период резкого движения вверх или вниз, свидетельствующего, как правило, о возникновении «критического» состояния в исследуемой системе); если р > 0,5, то как «флэт» (период относительного спокойствия). При р « 0,5 говорят о соответствии происходящих изменений броуновскому движению.

Согласно рисунку 3, в процессе нагружения вплоть до достижения образцом максимальных растягивающих напряжений, достигнутых через 127,83 секунды от начала испытания, наблюдается систематическое резкое снижение индекса фрактальности ниже уровня р = 0,5, что, на наш взгляд, связано с переходом системы в нестабильное состояние, связанное с формированием в структуре полимерного композита микроповреждений под действием растягивающих нагрузок. При этом до достижения композитом состояния разрушения работоспособность образца обеспечивается, в основном, за счет передачи нагрузки на зоны без микродефектов, что выражается на графике как повышение значений μ выше уровня 0,5. Следовательно, из анализа рисунка 3 можно выявить «критические» моменты нагружения, для которых индекс фрактальности будет принимать наименьшие значения. В данном случае для анализируемого полимерного образца подобные временные координаты, соответствующие точкам бифуркации, наступали (при μ < 0,4) через: 11,63; 41,02; 53,57; 59,77; 63,79; 78,80; 91,12; 101,71 и 103,14÷103,18 секунд от начала нагружения (см. точки на рис. 3). Наименьшие значения индекса фрактальности, соответствующие μ ≈ 0,32, зафиксированы через 81,17 и 103,15÷103,16 с (выделено точками красного цвета на рис. 3). Учитывая, что для всех исследуемых точек в области 103,14÷103,18 секунд наблюдается существенное снижение индекса фрактальности без его «восстановления» до значений 0,5 и более, все они были объединены под номером 10. Подобное последовательное падение μ в серии соседних точек свидетельствует о возникновении все больших «трудностей» при восприятии растягивающих напряжений образцом и начале процесса разуплотнения структуры, зарождении очагов локального разрушения, приводящих впоследствии к его разрушению. Числовые значения уровней напряжений и относительных деформаций в вышеперечисленных «критических» точках в абсолютных и относительных величинах (по отношению к точке достижения максимальных напряжений при растяжении) приведены в таблице 1.

^“уровень максимальных нагрузок О , • критические точки

Рис. 3. Изменение индекса фрактальности кривых деформирования эпоксидного полимера при растяжении в зависимости от длительности нагружения.

Таблица 1

Координаты «критических» точек кривой деформирования эпоксидного полимера при воздействии растягивающих нагрузок

Номер «критической» точки	Индекс фрактальности и	Параметры точек
		абсолютные величины			относительные величины
		^ крит. , с	^ крит. , МПа	^ крит. , %	^ крит. ^расг %	^ крит. ^ раст, %	^ крит. ^ раст. %
1	0,382	11,63	6,970	0,773	9.10	16.98	9.06
2	0,401	41,02	20,345	2,732	32.09	49.56	32.03
3	0,401	53,57	24,428	3,569	41.91	59.51	41.84
4	0,391	59,77	26,423	3,982	46.76	64.37	46.68
5	0,397	63,79	27,672	4,251	49.90	67.41	49.83
6	0,393	78,8	32,223	5,251	61.64	78.50	61.56
7	0,324	81,17	32,899	5,409	63.50	80.14	63.41
8	0,404	91,12	35,575	6,072	71.28	86.66	71.18
9	0,374	101,71	37,96	6,778	79.57	92.47	79.46
10	0,375	103,14	38,265	6,873	80.69	93.22	80.57
	0,327	103,15	38,265	6,874	80.69	93.22	80.59
	0,317	103,16	38,292	6,875	80.70	93.28	80.60
	0,355	103,17	38,309	6,875	80.71	93.32	80.60
	0,348	103,18	38,287	6,876	80.72	93.27	80.61

Предложенный подход для исследования механизма деформирования композиционных материалов при растяжении, осуществляемый на основе метода фрактального анализа кривых деформирования, регистрируемых с помощью современного испытательного оборудования с высокой частотой, позволяет получить ценную информацию о процессе накопления в его структуре микро- и макродефектов, приводящих к разрушению композитов. На наш взгляд, проведение подобных исследований на образцах полимерных композитов различного состава, а также после старения в условиях воздействия разнообразных агрессивных факторов, в том числе климатических, позволит получить ценную информацию о процессах, протекающих в структуре композиционных материалов при приложении растягивающих нагрузок.