Применение методов искусственного интеллекта для компьютерного моделирования фрактальных поверхностей
Автор: Сосенушкин Е.Н., Яновская Е.А., Желнов А.С.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 1 т.26, 2024 года.
Бесплатный доступ
В работе рассматривается возможность применения методов искусственного интеллекта для компьютерного моделирования фрактальных поверхностей. Фракталы выступают в качестве математической модели для создания случайного рельефа поверхности. Построение случайного профиля происходит с помощью метода случайных смещений, представляющего собой алгоритм генерации случайных функций со спектром. Поверхности задаются с помощью массивов данных, которые проходят проверку по условию самоподобия. На основе заданных массивов строятся модели с помощью функции Вейерштрасса. Алгоритм построения поверхностей был доработан и улучшен с помощью машинного обучения нейросетевой генеративной моделью. Таким образом, вместо простого создания фрактальной поверхности с использованием случайных функций, генератор создает фрактальные поверхности на основе распределения, изученного в процессе обучения. Критерием проверки является алгоритм, в основе которого заложен, в общем случае, математический метод Монте-Карло. Полученные результаты показывают реалистичность построенных фрактальных поверхностей с использованием нейронных сетей. Модели полученных рельефов поверхностей могут быть использованы при моделировании контактной механики, механики деформируемого твердого тела.
Искусственный интеллект, массив данных, рельеф поверхности, машинное обучение, компьютерное моделирование
Короткий адрес: https://sciup.org/148328541
IDR: 148328541 | УДК: 51-72 | DOI: 10.37313/1990-5378-2024-26-1-109-115
Текст научной статьи Применение методов искусственного интеллекта для компьютерного моделирования фрактальных поверхностей
EDN: LDTPQE
ПРИМЕНЕНИЕ ФРАКТАЛОВВ КОМПЬЮТЕРНОМ МОДЕЛИРОВАНИИ
Во многих трибологических исследованиях некоторые геометрические параметры, определяемые в евклидовом пространстве очень трудно измерить. Значения этих параметров увеличиваются при уменьшении масштаба измерения. Фрактальная геометрия может быть использована в качестве адаптированного пространства, в котором шероховатость может рассматриваться, как непрерывная, но недифференцируемая функция, а размерность D этого пространства является внутренним параметром, характеризующим рельеф поверхности. В данной работе фракталы выступают в качестве математической модели для построения случайного рельефа поверхности, которая может быть использована в качестве исходных данных
при моделировании механики деформируемого твердого тела.
Фрактал - геометрическая фигура, состоящая из частей, представляющих собой уменьшенную (необязательно точную) копию целого [1]. В свою очередь каждая часть разбивается на ещё меньшие копии до бесконечности. При этом фрактал является фигурой с дробным числом измерений, то есть не двухмерной и не трёхмерной, а, например, 1,5-мерной. На рис. 1 представлена модель фрактала, называемая

Рис. 1. Фрактальная модель с размерностью 1,585
треугольником Серпинского, с размерностью приближенно равной 1,585 [2].
Поверхности играют важную роль во множестве физических и трибологических разделах, таких как контактная механика, трение, износ, и т.д. Рельеф поверхности приводит к образованию дискретных точек контакта, когда две шероховатые, номинально плоские, поверхности сближаются, реальная площадь контакта складывается из площади отдельных точек контакта. Для большинства металлов при нормальных нагрузках эта площадь составляет лишь небольшой процент от видимой площади контакта. Типичные модели деформации поверхности являются либо упругими, либо пластическими, либо упругопластическими и могут быть представлены в виде функций поверхности и констант материала [3].
С другой стороны, основные статистические параметры шероховатости, такие как высота, наклон и кривизна, к сожалению, не всегда независимы от масштабов длины. Неточности в определении наклона или вершины шероховатости поверхности систематически обуславливаются самим процессом измерения, а не характеристиками поверхности. Следовательно, приборы с разным разрешением и длиной сканирования дают разные значения этих статистических параметров для одной и той же поверхности. Поэтому очень важно характеризовать шероховатые поверхности с помощью собственных параметров, которые не зависят от длины или площади выборки. Именно для этого используется фрактальная геометрия, моделирование поверхностей которой описывается в предложенной работе.
МАТЕМАТИЧЕСКИЙ АППАРАТ
ДЛЯ ПОСТРОЕНИЯ ФРАКТАЛЬНЫХ ПОВЕРХНОСТЕЙ
Для генерации случайных профилей и поверхностей используется метод случайных смещений, который моделирует случайную функцию со спектром. Этот алгоритм для построения модели фрактальной поверхности, в улучшенном с помощью машинного обучения виде, рассматривается в данной работе.
Для построения используются массивы данных такие же, как и в большинстве сканирующих методов получения изображений реального диапазона, а именно массив из 2 значений: Z (x, y). Алгоритм метода случайных смещений шероховатых поверхностей математически описывается следующим образом. Массив элементов Z(x) зависит от масштаба длины. Предполагается, что каждый элемент массива Z(x) является непрерывной, но недифференцируемой функцией. Это означает, что наличие сколь угодно малых элементов шероховатости может помешать нам достичь удовлетворительного предела:
[Z(x + A) - Z(x)]
A
,при A^ 0 .
Поэтому для построения модели, достаточно, чтобы в каждой точке выполнялось условие самоподобия:
|Z(x + A) - Z(x)| к A -- , 0 < H < 1, при A> 0, (2) и существовал предел lim AH-1 . В данном случае параметр H характеризует переход от непрерывной к дифференцируемой функции.
Если рассмотреть производную Z пропорциональную пределу представленной функции, то:
-
- при 0 < H < 1 , производная равна бесконечности и функция остается непрерывной;
-
- при H = 0 , функция становится прерывной.
Таким образом, изменяя параметр H от 0 до 1, параметр H характеризует переход от непрерывной к дифференцируемой функции, причем диапазон 0 < H < 1 соответствует недифференцируемым функциям, которые становятся более гладкими с увеличением H . Следовательно, H можно рассматривать, как показатель шероховатости. Поскольку речь идет о функциях, представляющих собой случайные процессы, мы выражаем отношение самоподобия следующим образом:
[(Z(x + A) - Z(x))2] к A2H, 0 < H < 1-при A^ 0 . (3)
Это соотношение можно обобщить на размерность евклидова пространства E>1 :
[(Z(z + A) -Z(x))2] к ||A||2H,0 < H < 1,при A^ 0 . (4)
В этом случае x представляет собой точку в E -мерном евклидовом пространстве R E , а || || является нормой этого пространства.
Во многих исследованиях уже проводилось построение поверхностей с помощью функции Вейерштрасса [4-8]:
co v-1 cos(2^knx + m„)
Z „ (x) .1 ^ —— —, где к > 1,0 < H < 1, (5) n^n 1
где A – масштабирующая константа, k – произвольное нечетное число.
Кроме того, функцию можно представить в следующем виде [6]:
c-' cos{2reknx + ^n}cos{2rekny + ^n}
Z(x,y) - A ^ -------------k ^S------------- . (6)
П=П 1
Следует отметить, что сами модели поверхностей, построенные с помощью функции Вейерштрасса, не являются фрактальными ввиду того, что отсутствует изотропность результата. Следовательно, важнейшим пунктом в построении является применение метода случайных смещений, описанного ранее, и проверка массива данных с помощью критерия самоподобия.
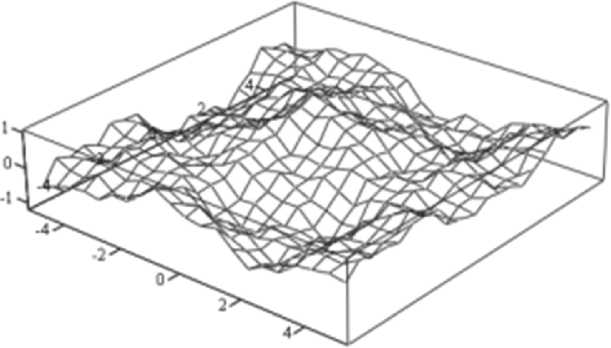
Рис. 2. Смоделированная фрактальная поверхность
Также следует отметить, что фактически для моделирования требуется 3 основных параметра:
-
. параметр H характеризующий фрактальную размерность;
. начальное среднеквадратичное отклонение;
. число точек моделирования для поверхности.
Полученная фрактальная модель представлена на рис. 2.
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ РЕЛЬЕФОВ С ПОМОЩЬЮ НЕЙРОСЕТЕВОЙ
МОДЕЛИ
Для моделирования фрактальных поверхностей с применением машинного обучения было принято решение использовать язык программирования Python. Кроме того, были задействованы следующие библиотеки:
. NumPy;
. Matplotlib;
. Keras.
Такой выбор обосновывается тем, что NumPy поддерживает многомерные массивы и высокоуровневые математические функции для работы с этими массивами. Matplotlib позволяет строить точную визуализацию построенных моделей, а библиотека Keras была задействована для машинного обучения. В качестве обучающего алгоритма использовалась генеративная модель обучения [9-10], чтобы генерировать новые фрактальные поверхности. Вместо простого создания фрактальной поверхности с использованием случайных точек, генератор создает фрактальные поверхности на основе распределения, изученного в процессе обучения.
Генеративные модели считаются достаточно новым и перспективным подходом к глубокому машинному обучению. Модель используется для генерации новых данных, с точки зрения вероятностных моделей. В основе моделирования лежит подбор новых данных по основному признаку или ряду признаков.
В работе для обучения использовалась функция GAN, создавая генеративные модели по следующему алгоритму:
-
1) Генерация случайного шума для входа генератора;
-
2) Создание фальшивых образов;
-
3) Создание настоящих образов;
-
4) Обучение дискриминатора на настоящих и фальшивых образах.
Построение фрактальных поверхностей происходило с помощью математического аппарата, описанного в работе и машинного обучения на генеративных моделях. Блок-схема работы программы для построения фрактальных моделей представлена на рис. 3.
Таким образом, модель уже на текущем этапе показала свою эффективность, в сравнении с методом случайных смещений ввиду того, что при построении поверхности с помощью генеративного метода, модель не требует дополнительной проверки на самоподобие. Генерация происходит на основе тех признаков, которые задаются изначально, что в разы увеличивает скорость построения, уменьшает ресурсоем-кость программы и облегчает пользователю само построение фрактальной поверхности.
Фрактальная поверхности, построенная в совокупности двух описанных в работе методов представлена на рис. 4 (а). На рис. 4 (б) показаны параметры поверхности 2D вида.
Использование предложенного метода для создания шероховатых поверхностей с фрактальной размерностью, приводит к получению контура с желаемым уровнем шероховатости. На рис. 4 видны гладкие участки и пики, которые использовались для оценки точности построенной модели по отношению к выборке генеративных моделей. Оценка происходит с помощью среднеквадратичного отклонения, и представлена в таблице 1 [11-12].
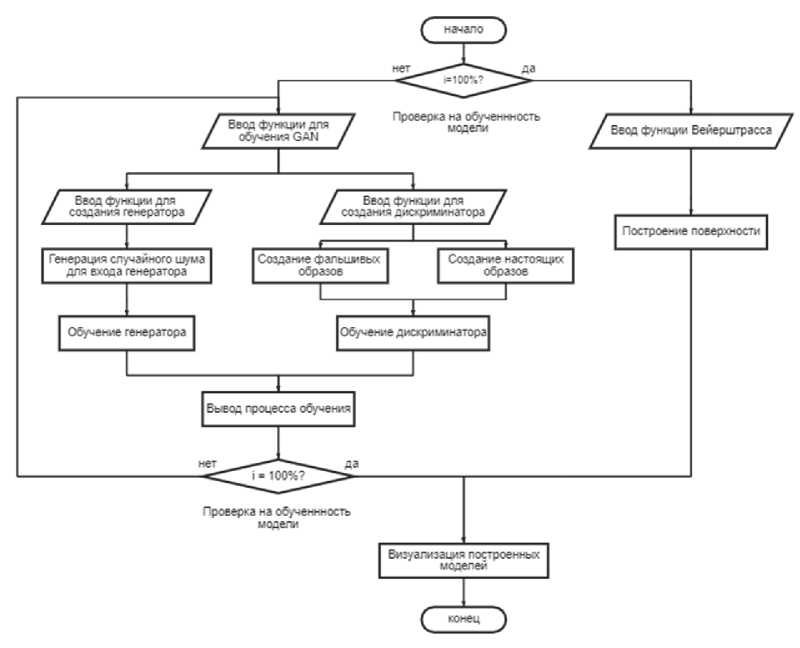
Рис. 3. Блок-схема построения моделей
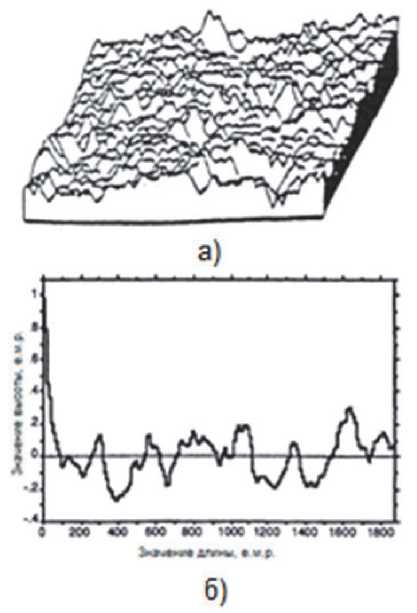
Рис. 4. Модели фрактальных поверхностей, построенных с применением методов искусственного интеллекта
Значение ошибки не превышает 10% по отношению к единице. Можно сделать вывод, что генеративный алгоритм машинного
Таблица 1. Среднеквадратическая ошибка модели для 10 поверхностей
|
№ |
Значение среднеквадратической ошибки |
|
1 |
0,034 |
|
2 |
0,085 |
|
3 |
0,074 |
|
4 |
0,051 |
|
5 |
0,038 |
|
6 |
0,047 |
|
7 |
0,072 |
|
8 |
0,037 |
|
9 |
0,048 |
|
10 |
0,071 |
обучения в применении к построению моделей фрактальных поверхностей является точным.
Таблица 2. Отклонение 15 точек максимумов
|
№ |
Обученная модель |
Оценочная модель |
Модуль разности |
|
1 |
0,983 |
0,978 |
0,005 |
|
2 |
0,547 |
0,543 |
0,004 |
|
3 |
0,672 |
0,678 |
0,006 |
|
4 |
0,991 |
0,985 |
0,006 |
|
5 |
0,479 |
0,470 |
0,009 |
|
6 |
0,865 |
0,877 |
0,012 |
|
7 |
0,341 |
0,354 |
0,013 |
|
8 |
0,447 |
0,459 |
0,012 |
|
9 |
0,788 |
0,783 |
0,005 |
|
10 |
0,879 |
0,877 |
0,002 |
|
11 |
0,375 |
0,376 |
0,001 |
|
12 |
0,541 |
0,535 |
0,006 |
|
13 |
0,877 |
0,870 |
0,007 |
|
14 |
0,253 |
0,241 |
0,012 |
|
15 |
0,348 |
0,344 |
0,004 |
ПРОВЕРКА ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ НА РЕАЛИСТИЧНОСТЬ
Для оценки реалистичности построенной модели фрактальной поверхности в качестве проверяющего фактора была использована мера отклонения точек максимума построенной с помощью обучения поверхности от точек максимума сгенерированной заранее фрактальной поверхности. Для нахождения значений экстремумов применялся метод Монте-Карло [13-14]. Результаты оценки представлены в таблице 2.
На рис. 5 приведена смоделированная фракталь- ная поверхность с применением генеративного алго- ритма, использованная для оценки реалистичности.
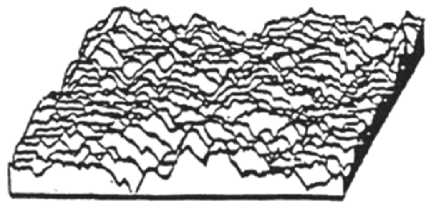
Рис. 5. Модель фрактальной поверхности, использованная для оценки реалистичности
Полученные результаты показывают, что фрактальная модель реалистична, а фрактальная размерность может быть использована в качестве реальных значений различных масштабно-зависимых параметров, таких как длина поверхности и объем шероховатости. В дальнейшем рассматривается возможность применения фрактальных поверхностей, полученных с помощью методов искусственного интеллекта, для моделирования износа и контакта рельефов различной жесткости друг с другом, а также проведение натурных экспериментов с использованием компьютерных моделей.
Список литературы Применение методов искусственного интеллекта для компьютерного моделирования фрактальных поверхностей
- Бекман, И.Н. Геометрия фракталов. Курс лекций / И. Н. Бекман. – М.: Московский государственный университет им. М.В. Ломоносова, 2010. – 29 с.
- Бекман, И.Н. Нелинейная динамика сложных систем: теория и практика/ И. Н. Бекман. – М.: Московский государственный университет им. М.В. Ломоносова, 2018. – 132 с.
- Стружанов, В.В. Теория упругости: основные положения: учеб. пособие / В.В. Стружанов, Н.В. Бурмашева; М-во науки и высш. образования Рос. Федерации, Урал. федер. ун-т. – Екатеринбург: Изд-во Урал. ун-та, 2019. – 204 с.
- J. J. Gagnepin and C. Roques-Carmes, Practal approach to two-dimensional and three-dimensional surface roughness, 109, 114-119 (1986).
- A. Majunder and B. Bhushan, Role of fractal geometry in roughness characterization and contsct mechanics of surfaces, ASME J. Tkibology, 112, 205-216 (1990).
- A. Majunder and C.L. Tien, Fractal charscterization and simulation of rough surfaces, 136, 313-327 (1990).
- A. Majunder and B. Bhushan, Fractal model of elasticplastic contact between rough surfaces, J. Zkibology, 13, l-11 (1991).
- J. Lopez, G. Hansali, H. Zahouani, J.C. Lebosse and T. Mathia, 3D fractal-based characterization for engineered surface topography, Int. J. Mach. Tools Manufact, 35, 211-217 (1995).
- Дэвид Фостер. Генеративное глубокое обучение. Творческий потенциал нейронных сетей. — СПб.: Питер, 2020. — 336 с.: ил. — (Серия «Бестселлеры O’Reilly»).
- Гафаров, Ф.М.. Искусственные нейронные сети и приложения: учеб. пособие / Ф.М. Гафаров, А.Ф. Галимянов. – Казань: Изд-во Казан. ун-та, 2018. – 121 с.
- Кравченко, Н.С. Методы обработки результатов измерений и оценки погрешностей в учебном лабораторном практикуме: учебное пособие; издание второе / Н.С. Кравченко, О.Г. Ревинская; Национальный исследовательский Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2017. – 121 с.
- Трофимова, Е.А. Теория вероятностей и математическая статистика: учеб. пособие / Е. А. Трофимова, Н. В. Кисляк, Д. В. Гилёв; [под общ. ред. Е. А. Трофимовой]; М-во образования и науки Рос. Федерации, Урал. федер. ун-т. – Екатеринбург: Изд-во Урал. ун-та, 2018. – 160 с.
- Раменская, А.В. Метод Монте-Карло и инструментальные средства его реализации: методические указания / А.В. Раменская, К.В. Пивоварова; Оренбургский гос. ун-т. – Оренбург: ОГУ, 2018. – 58 с.
- Михайлов, Г.А. Статистическое моделирование. Методы Монте-Карло: учебное пособие для вузов / Г. А. Михайлов, А. В. Войтишек. – М.: Юрайт, 2024. – 323 с.


