Применение методов кластерного анализа для динамической коррекции области поиска в генетическом алгоритме

Генетические алгоритмы (ГА) зарекомендовали себя как универсальный инструмент для решения сложных задач глобальной оптимизации в различных областях науки и техники. В ракетно-космической отрасли они применяются для проектирования систем управления [1], оптимизации параметров двигательных установок, аэродинамических форм крыльев и обтекателей, траекторий полёта и систем жизнеобеспечения космических аппаратов [2], а также во многих других задачах. Классическая реализация ГА предполагает фиксированные границы областей поиска для каждой переменной, что на ранних этапах может приводить к избыточному исследованию бесперспективных участков n -мерного пространства и замедлять процесс сходимости.

Одним из приоритетов последних модификаций стало сокращение объёма вычислений за счёт более экономного распределения ресурсов и фокусировки на действительно значимых участках пространства решений. Для этого используются различные подходы: адаптация параметров в процессе эволюции, обучение выбору вариантов операторов на данных предыдущих поколений, а также динамическая локализация поиска с учётом текущего распределения решений. Всё это может позволить ускорить сходимость и повысить эффективность поиска без существенного роста вычислительной нагрузки.

В данной работе предложен метод динамической коррекции области поиска генетического алгоритма, отличающийся от известных реализацией процедуры итеративной кластеризации популяции с последующим удалением неперспективных кластеров, что позволяет эффективно адаптировать область поиска и повысить скорость сходимости к оптимальному решению. Суть метода заключается в том, что после каждого шага селекции популяция разбивается на группы с использованием одного из алгоритмов кластеризации. В настоящей работе исследовано применение 5 подходов: с заранее определенным количеством кластеров – k-средних, k-медианных, агломерированная и спектральная кластеризация, а также подход с динамически определяемым количеством кластеров DBScan. Для каждого кластера вычисляются показатели численности индивидов и их средней пригодности. Кластеры, одновременно не достигшие пороговых значений по критериям возможности коррекции поискового пространства и останова, полностью исключаются из дальнейшего поиска, а области переменных корректируются с учётом распределения оставшихся индивидов.

Основная цель исследования – повысить скорость сходимости без ухудшения качества найденного решения, что важно при сложных инженерных расчётах в области проектирования ракетно-космической систем. В статье приводится математическая постановка задачи, описание процедуры кластеризации и фильтрации, а также результаты вычислительных экспериментов на стандартных тестовых функциях, демонстрирующие 25–30 % экономии вычислительных ресурсов по сравнению с классическим ГА.

Обзор существующих методов

В последние годы появилось немало модификаций для ГА, направленных на повышение их гибкости и исключение преждевременной сходимости к локальным экстремумам. Одна из ключевых тенденций – внедрение автоматической адаптации параметров. Вместо жёстко заданных вероятностей мутации и скрещивания, современные алгоритмы оценивают «разнообразие» популяции (например, через генетическую энтропию или дисперсию) и динамически изменяют эти вероятности. В ряде реализаций сама величина шага мутации эволюционирует вместе с решением (self-adaptive подход), что избавляет от длительной настройки на этапе подготовки и помогает избегать преждевременного сжатия популяции [3].

Вместе с этим всё большее распространение получили многопопуляционные, или «островные», модели ГА. В традиционном ГА существует единственная популяция, но в современных реализациях исследователи стали создавать сразу несколько небольших субпопуляций («островов»), каждая из которых эволюционирует относительно автономно [4]. Периодически между островами происходит миграция индивидов: лучшие особи перетекают в другие популяции, что позволяет сочетать преимущества параллельного исследования различных регионов пространства решений и обмена качественными генами [5].

Немалую роль в развитии ГА сыграла интеграция с локальными методами оптимизации, породив меметические алгоритмы (т. н. memetic algorithms). Идея заключается в том, что генетический оператор глобального поиска дополняется мощными процедурными локальными «до-исследованиями», например, градиентными спусками, где это возможно, или алгоритмами прямого локального поиска в случае отсутствия информации о производных. В результате ГА проводит широкое «сканирование» пространства, а локальные алгоритмы обеспечивают улучшение значения пригодности перспективных индивидов [6].

Помимо этого, многокритериальная оптимизация стала важным направлением для развития ГА, так как в реальных инженерных и экономических задачах необходимо учитывать сразу несколько конкурирующих целей. Хотя классические методы NSGA-II [7], MOEA/D [8] и SPEA2 [9] прочно утвердились, в последние годы специалисты предложили новые стратегии для лучшего распределения решений фронта Парето. Например, адаптивное распределение опорных точек (reference points) позволяет более равномерно представлять разные области фронта, а динамическая «ширина окна» (crowding distance) учитывает локальную плотность решений: если решения скапливаются слишком плотно, алгоритм автоматически расширяет расстояние разделения, тем самым стимулируя поиск в менее исследованных областях [10].

Активно развивается направление суррогатного моделирования, где вычисления целевой функции заменяются предиктивными моделями (Gaussian Process, случайный лес, нейросети). В гибридных схемах Surrogate-Assisted GA (SA-GA) сбор данных о целевой функции идёт постепенно: вначале строится простой суррогат, а затем, по мере накопления данных, алгоритм переобучает модель [11].

Наконец, нельзя не упомянуть об интеграции ГА с нейроэволюционными методами, где алгоритм не только оптимизирует веса нейросети, но и её топологию. Изначально предложенный NEAT (NeuroEvolution of Augmenting Topologies [12]) получил новое дыхание в сочетании с современными архитектурами (сверточные сети, трансформеры) [13]. В Deep Neuroevolution GA оператор мутации может добавлять или удалять слои нейросети, а кроссовер «скрещивает» архитектуры, стремясь получить компромисс между точностью и компактностью. Такие подходы активно применяются в AutoML-пайплайнах, где автоматическое проектирование нейросетей позволяет сократить время и усилия инженера на ручную настройку.

Однако вопросам коррекции областей поиска не уделяется достаточного внимания [14], что подтверждает актуальность разработки современных схем повышения скорости сходимости ГА за счет концентрации вычислительных ресурсов в перспективных регионах.

Математическая постановка задачи

Рассматривается задача глобальной оптимизации многомерной функции вещественных переменных на ограниченной области определения. Пусть X – вектор переменных, характеризующий пространство поиска:

X = { X i , i = 1, ..., n},                                               (1)

где n – размерность задачи (количество переменных целевой функции), x i – i -я переменная. Для каждой переменной задана начальная область определения:

x i ^e D xi =[ x l , x h ] ,                                          ⁽²⁾

где x_i^l и x_i^h – нижняя и верхняя границы области допустимых значений переменной x i . Эти границы определяют начальную гиперпараллелепипедную область поиска в n -мерном пространстве.

В классических вариантах генетических алгоритмов предполагается [15; 16], что границы D_xi остаются постоянными на протяжении всего процесса эволюции:

D_x - фиксировано, V i = 1, ..., n .                               (3)

x _i

Однако такое допущение может быть неэффективным, поскольку оно не позволяет учитывать изменяющуюся структуру распределения решений в процессе поиска. В настоящей работе предлагается и исследуется метод динамической коррекции области поиска генетического алгоритма на каждом его поколении.

Для формализации предлагаемого подхода введём следующие обозначения:

G – общее количество поколений (итераций) генетического алгоритма;

g - номер текущего поколения, g = {1,2, _, G };

M – количество индивидов (решений) в популяции на каждом поколении;

m - индекс конкретного индивида в популяции, m = {1,2, ..., M };

K – число кластеров, полученных после кластеризации популяции;

k - индекс кластера, к = {1,2, ., K } ;

Ind_m ^g – вектор параметров m -го индивида на поколении g ;

F _g – значение функции пригодности (fitness) для индивида Ind_m^g ;

Ind _m

IndSet_k^g – множество всех индивидов, принадлежащих кластеру k на поколении g ;

M kg = ( IndSet f ) – количество индивидов в кластере k на поколении g .

Каждому кластеру k на поколении g сопоставляется собственная область определения для каждой переменной x_i (рис. 1), которую обозначим:

D^{g , k} = [ x ^g ’ ^{k ;} l , x ^g ’ ^k;^h

где x _i ^{g , k ; l} и x _i ^{g , k ; h} – текущие нижняя и верхняя границы переменной x_i в кластере k на поколении g .

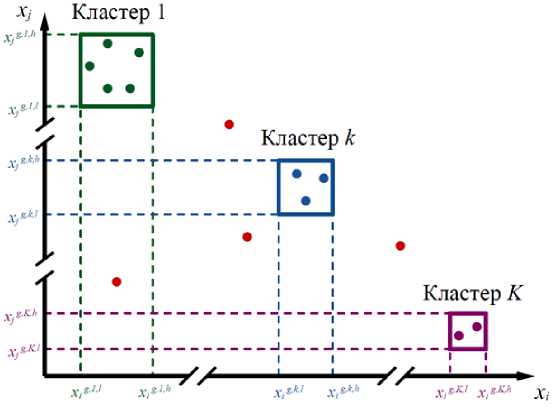
Рис. 1. Схема кластеризации

Fig. 1. Clustering diagram

Полная область поиска по переменной x_i на поколении g определяется как объединение по всем кластерам (5):

K

_Dxg_{i = ∪ Dx}g_i,k_{.                                     (5)}

k = 1

Если кластер признаётся неэффективным (по критериям, описанным далее), соответствующая область D_x^g_i ^{, k} исключается из рассмотрения, т. е. полагаем:

D^{g , k} = 0 .

x _i

Кластеризация решений

Плотностные алгоритмы не требуют предварительного задания количества числа кластеров – DBScan определяет кластеры как области с минимальным числом соседей на расстоянии не более ε (параметра, который задает пользователь), автоматически отбрасывая разреженные точки как шум.

Перед кластеризацией необходимо нормализовать данные (привести каждый признак к единому масштабу, например [0,1], и выбрать метрику (евклидова или манхэттенская), поскольку различие диапазонов переменных и способ вычисления расстояний существенно влияет на структуру кластеров.

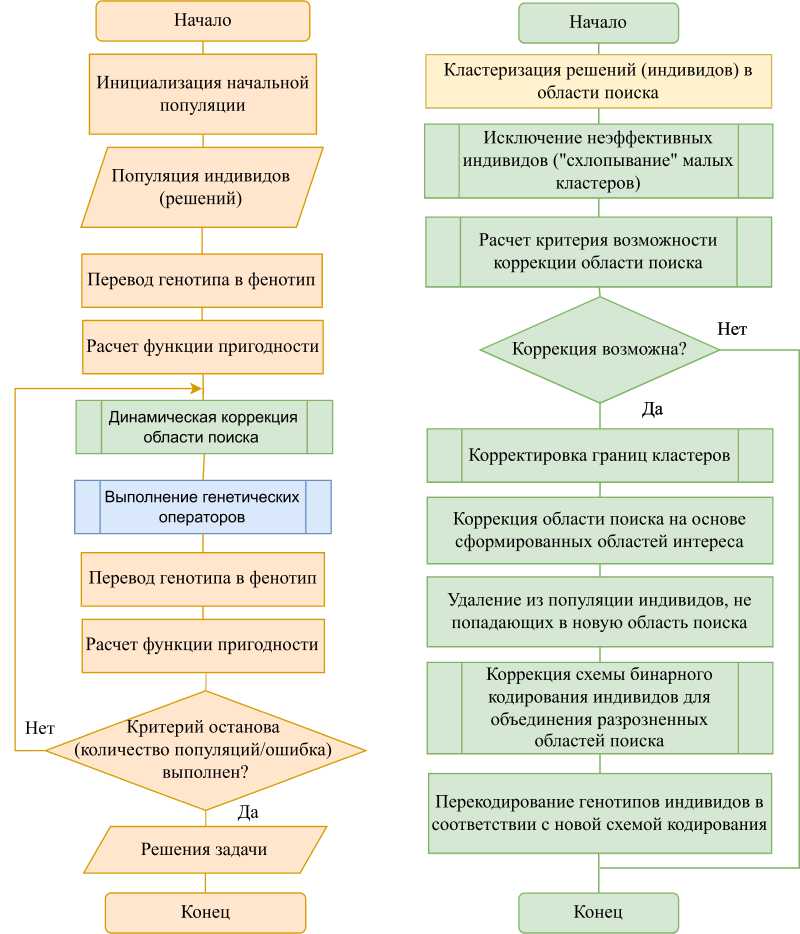
a                                      б

Рис. 2. Блок-схема:

а – ГА с динамической коррекцией области поиска; б – процедуры динамической коррекции

Fig. 2. Block diagram:

а – GA with dynamic correction of search area; б – block diagram of the dynamic correction procedure

В алгоритме оптимизации (рис. 2) результаты кластерного разбиения используются для локальной корректировки границ областей поиска: в каждом кластере вычисляются корректирующие смещения на основе статистик распределения индивидов, что позволяет сузить или расширить область исследования вокруг перспективных решений. Кроме того, внутри кластеров повышается вероятность рекомбинации ближайших представителей, что помогает сохранять локальные особенности найденных оптимумов, а вычислительные ресурсы динамически перераспределяются в пользу кластеров с более высоким качеством решения или скоростью сходимости. Такой подход обеспечивает сбалансированное сочетание исследования и использования пространства решений и способствует более быстрой и надёжной сходимости алгоритма.

Коррекция границ кластеров

После того, как сформированы кластеры, выполняется процедура коррекции границ области поиска в каждом из них, которая производится на основе анализа распределения индивидов внутри кластера. Формально, границы области D_xg_i ^{, k} обновляются следующим образом:

_Dg , k ₌ x _i

у g, k; l + л Yg, k; h + л xi +Δ g,k;l , xi     +Δ g,k;h , xig                    xg

где A k l^ g R и A k h. _h g R - корректирующие значения, на основе которых могут как расши- _xi g , ;                    _xi g , ;

ряться, так и сужаться исходные границы. Они могут быть получены на основе стандартного отклонения значений переменной x_i внутри кластера.

Таким образом, на каждом поколении осуществляется локальная адаптация границ области поиска с целью сосредоточения вычислительных ресурсов на перспективных регионах пространства решений.

Реализация и обсуждение

Метод был протестирован на наборе из 4 стандартных тестовых функций различной размерности [18]. Эффективность подхода далее иллюстрируется на примере четырех тестовых функций Экли, Били, Бута и Букина № 6, поскольку они образуют репрезентативную выборку для комплексной оценки эффективности оптимизационных алгоритмов. Ключевое преимущество данного набора функций заключается в том, что они обладают наиболее репрезентативным набором свойств, представляющих наибольшую сложность для алгоритмов оптимизации.

Функция Экли (Ackley) представляет собой сложную многомодальную поверхность с большим количеством локальных минимумов, что позволяет проверить способность алгоритма избегать преждевременной сходимости к субоптимальным решениям:

f ( x ) = - 20exp

- 0,2

\

n

1 Z Х 2 n i = 1

л

/

-

Г1A z exp -^cos(2nx ) + 20 + e.

I n%

Функция Били (Beale) имеет высокую чувствительность к выбору начальной точки:

d

F ( x ) = E ( 1,5 - x i = 1 -

^: 2 i - 1 ⁺ x 2 i - 1 x 2 i ) ⁺( ²,²⁵ x 2 i - 1 ⁺ x 2 i - 1 x 2i ) ⁺( ²,6^{25 x} 2 i - 1 ⁺ x 2 i - 1

„3 \^{2 x 2} i ) ,

f ( x , y ) = ( x + 2 y - 7 ) ² + ( 2 x + y - 5 ) ² .

Функция Букина № 6 (Bukin № 6), благодаря наличию разрывов и характерным «оврагам», позволяет оценить устойчивость алгоритмов к экстремальным изменениям градиента:

f ( x , y ) = 100 ^ ( y - 0,01 x ²) + 0,01 ( x + 10 ) .                        (11)

Изображения изолиний вышеуказанных тестовых функций для случая двух переменных

представлены на рис. 3.

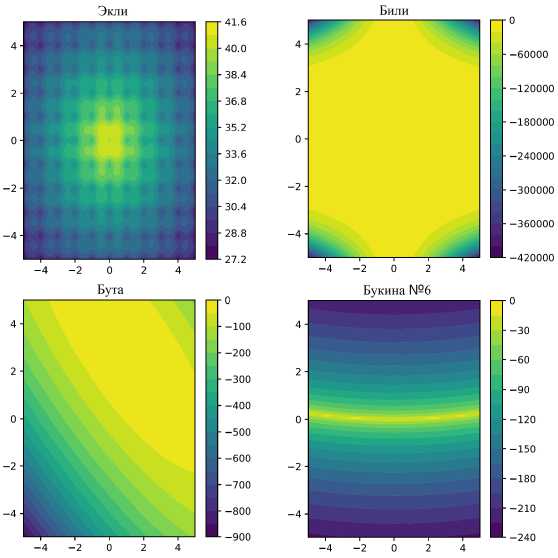
Рис. 3. Изолинии тестовых функций

Fig. 3. Contour plots of test functions

На рис. 4 представлена визуализация оценки эффективности предлагаемого подхода на примере вышеуказанных функций для функций Экли, Били, Бута, Букина № 6 соответственно. Выбор обусловлен различной природой этих тестовых задач: функция Экли традиционно используется как эталон для проверки масштабируемости методов оптимизации в пространстве большой размерности; многомерная модификация функции Били позволяет оценить поведение алгоритма на средних размерностях с выраженной зависимостью от начальных условий; функции Бута и Букина № 6 являются двумерными по определению и применяются для базовой валидации корректности и устойчивости метода в условиях простого (для Бута) и резко изменяющегося (для Букина № 6) рельефа целевой поверхности. На рис. 4 представлены результаты применения пяти методов кластеризации: k-средних (k-means), k-медианных (k-medians), DBSCAN, агломератив-ной кластеризации и скользящего среднего от верхнего к нижнему ряду соответственно.

Из рис. 4 видно, что для сложных многомерных функций (Ackley, Beale) наилучшие результаты достигаются при использовании 3–6 кластеров, где медианные значения числа итераций ниже и разброс меньше. Для двумерных функций (Booth, Bukin № 6) влияние параметра минимально, поэтому достаточно 1–2 кластеров без заметной потери качества.

На основании прогонов алгоритма на двумерных тестовых функциях, описанных выше, было выявлено, что оптимальный диапазон числа кластеров для большинства задач находится в пределах 3–6. Для анализа многомерных тестовых функций использовался метод k-means, обеспечивающий стабильное разделение точек и ускорение сходимости алгоритма.

В табл. 1 представлены средние значения числа вычислений целевых функций с указанием стандартного отклонения при различных размерностях и числе кластеров. Функции выбраны из стандартного набора тестовых функций, которые допускают обобщение на пространства большей размерности.

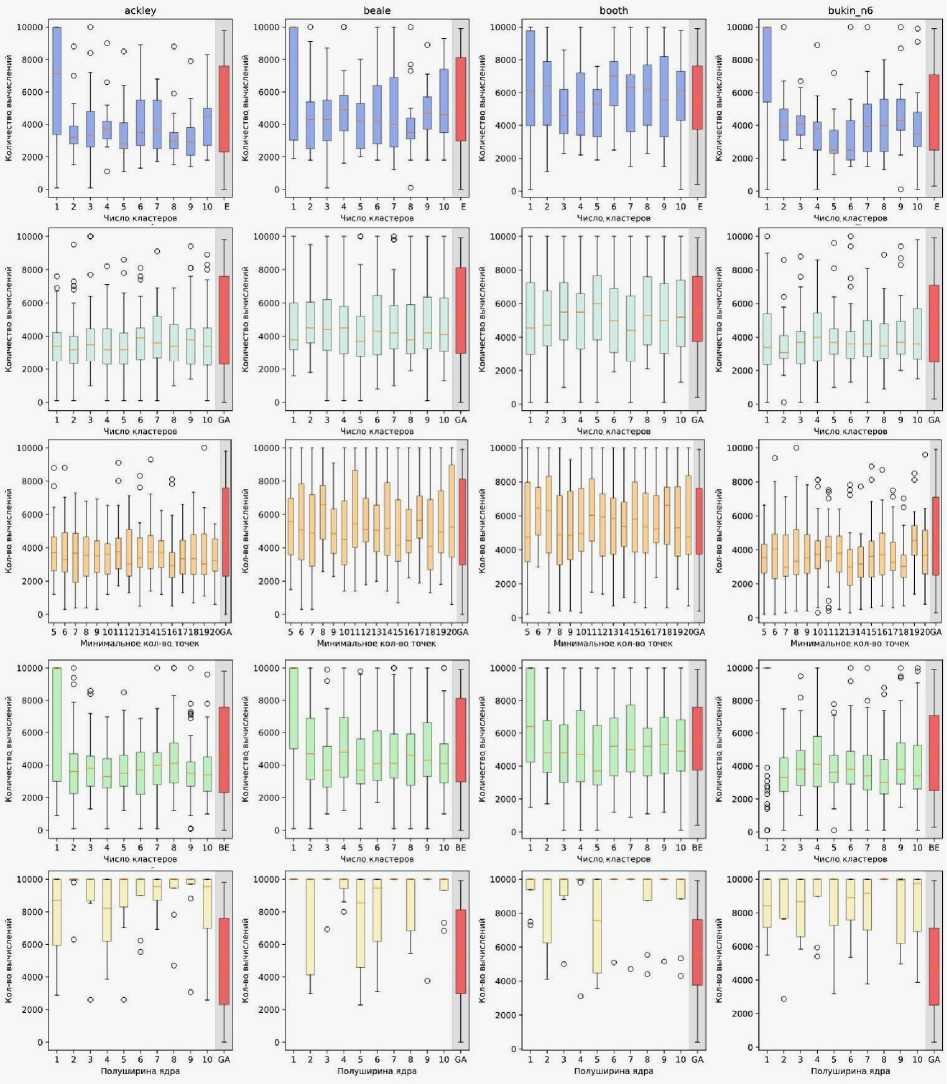
Рис. 4. Диаграммы межквартильного размаха результатов экспериментов. Представлены результаты применения пяти методов кластеризации: k-средних (k-means), k-медианных (k-medians), DBSCAN, агломеративной кластеризации и скользящего среднего (от верхнего к нижнему ряду, соответственно)

Fig. 4. Interquartile (IQR) range diagrams of the experimental results. The figure shows the outcomes of five clustering methods: k-means, k-medians, DBSCAN, agglomerative clustering, and moving average (from top to bottom row, respectively)

Таблица 1

Среднее количество вычислений целевой функции (± стандартное отклонение) для многомерных тестовых функций при различной размерности и числе кластеров

Функция	Размерность	3 кластера	4 кластера	5 кластеров	6 кластеров
Сфера	10	1187 ± 132	2295 ± 214	2478 ± 289	2221 ± 367
	20	2644 ± 305	5548 ± 412	4822 ± 497	4133 ± 721
	50	4758 ± 623	10187 ± 807	11643 ± 1002	11387 ± 1154
	100	9442 ± 1189	8921 ± 1030	8737 ± 1655	9845 ± 2033
Розенброк	10	3368 ± 247	3124 ± 301	4192 ± 382	4087 ± 472
	20	5278 ± 493	4842 ± 615	5217 ± 786	6462 ± 912
	50	8956 ± 1044	8682 ± 1218	8447 ± 1659	8973 ± 1187
	100	10671 ± 2047	11348 ± 1965	10582 ± 2954	12791 ± 3092
Растригина	10	4142 ± 198	4084 ± 153	4226 ± 433	4211 ± 498
	20	6637 ± 527	6438 ± 642	6582 ± 804	6276 ± 986
	50	9672 ± 1810	9452 ± 1551	9911 ± 2792	9374 ± 2025
	100	16941 ± 2647	15482 ± 3082	12653 ± 3467	13278 ± 3065
Экли	10	3885 ± 107	3851 ± 286	3682 ± 154	3718 ± 449
	20	9154 ± 554	9247 ± 718	10368 ± 601	9012 ± 1802
	50	15934 ± 1087	17614 ± 2762	15761 ± 2634	16286 ± 2089
	100	22184 ± 2794	20378 ± 3358	19756 ± 3841	20187 ± 2712
Стыбинского-Танга	10	4082 ± 103	3738 ± 214	4187 ± 478	3724 ± 251
	20	6326 ± 389	6843 ± 518	7624 ± 967	6557 ± 842
	50	10762 ± 895	10574 ± 1128	11198 ± 1376	10867 ± 1582
	100	20468 ± 1836	21328 ± 1215	21642 ± 2048	18124 ± 3096

Из табл. 1 видно, что в большинстве случаев меньшее число вычислений целевой функции достигается при 3–4 кластерах, особенно для низкой размерности. При высокой размерности влияние числа кластеров менее выражено, однако диапазон 3–6 кластеров остаётся эффективным.

На материале использованных тестовых функций видно, что правильный подбор числа кластеров k может кардинально менять число поколений до сходимости к глобальному оптимальному решению с предлагаемой модификацией. Во всех случаях ключевыми факторами являются:

• -    сложность ландшафта целевой функции (наличие локальных минимумов и их плотность, узкие или широкие зоны притяжения);

• -    адекватность выбора k (малое k не позволяет выделить все «горячие» области, а слишком большое – приводит к перерасходу ресурсов);

• -    эффективность процедуры обновления границ областей поиска в каждом кластере обеспечивает быстрый «сдвиг» внимания алгоритма к перспективным регионам.

Такой баланс между исследованием пространства решений и использованием результатов исследования обуславливает ускоренную сходимость предложенной модификации по сравнению со стандартным подходом.

Также для сравнения эффективности предложенной в данной статье модификации ГА была проведена серия вычислительных экспериментов на наборе тестовых функций CEC 2017 [19]. В рамках экспериментов рассматривались четыре комбинации алгоритмов:

• –    стандартный ГА без модификаций;

• –    стандартный ГА с предложенной модификацией;

• –    алгоритм SelfCSHAGA (Self-Configuring Success History-based Adaptation Genetic Algorithm) [20];

• –    алгоритм SelfCSHAGA с предложенной модификацией.

В экспериментальном протоколе использовались тестовые функции из набора CEC’2017. Для каждой функции параметры были выбраны таким образом, чтобы обеспечить максимально возможную размерность задачи при сохранении адекватной вычислительной сложности и устойчивости работы алгоритма. В частности, для большинства функций применялась размерность 50 переменных и размер популяции 200 индивидов. Для более вычислительно слож- ных функций (например, f 4, f 5, f 7, f 8) размерность была снижена до 20 или 10. Следует отметить, что функция f 9 оказалась чувствительной к размерности: при увеличении размерности до 10 алгоритм SelfCSHAGA работает аналогично стандартному ГА. Однако при размерности 2 алгоритм достаточно быстро находил оптимум.

Количество итераций также адаптировалось в зависимости от сложности функции и размерности области поиска: от 100 итераций (для f 9) до 2000 итераций (для f 2). В табл. 2 приведены параметры экспериментов стандартного ГА и алгоритма SelfCSHAGA на тестовых функциях CEC’2017. Для каждой функции указаны размерность задачи, размер популяции, количество итераций, границы поиска и шаг дискретизации. Следует отметить, что на функциях f 1, f 2 и f 10 стандартный ГА не справился с поиском оптимума, тогда как SelfCSHAGA продемонстрировал успешную работу.

Таблица 2

Параметры экспериментов для GA и SelfCSHAGA (sSHAGA) на функциях CEC’2017

Функция	Размерность D (GA)	Размерность D (sSHAGA)	Поколение (GA)	Поколение (sSHAGA)	Популяция (GA)	Популяция (sSHAGA)	Границы поиска	Оптимальное значение
f 1	–	50	–	1100	–	200	[–100, 100]	100
f 2	–	50	–	2000	–	200	[–100, 100]	200
f 3	20	50	4500	1000	100	200	[–100, 100]	300
f 4	10	20	3500	1000	100	200	[–100, 100]	400
f 5	10	20	3500	1300	200	200	[–100, 100]	500
f 6	20	50	2500	300	100	200	[–100, 100]	600
f 7	10	20	2500	500	100	400	[–50, 50]	700
f 8	10	10	3500	1100	300	100	[–50, 50]	800
f 9	2	2	100	100	100	50	[–10, 10]	900
f10	–	10	–	2500	–	200	[–100, 100]	1000

С теми же настройками были протестированы и алгоритмы с модификацией, предложенной в данной статье. Использовался кластеризатор K-means с числом кластеров от 3 до 6. Анализ распределения количества вычислений целевой функции проведён на основе межквартильного размаха. Для стандартного ГА наблюдается вариативность вычислительных затрат между функциями (рис. 5 и 6).

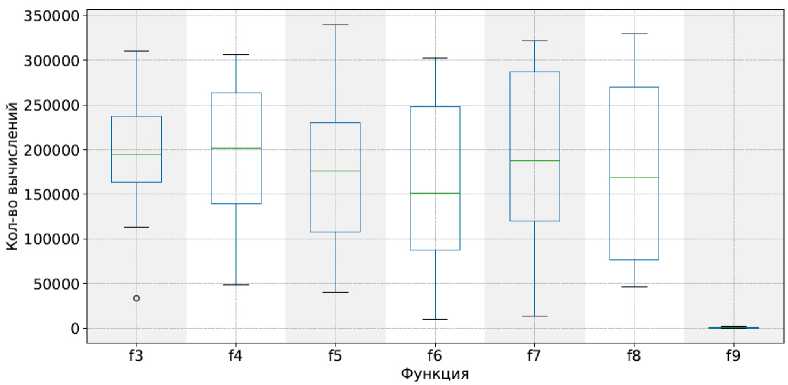
Рис. 5. Диаграммы межквартильного размаха для функций f 3– f 9. По оси ординат показано количество вычислений целевой функции. Результаты получены с использованием стандартного генетического алгоритма

Fig. 5. Boxplot diagrams for functions f 3– f 9. The y-axis shows the number of objective function evaluations. The results were obtained using the standard genetic algorithm

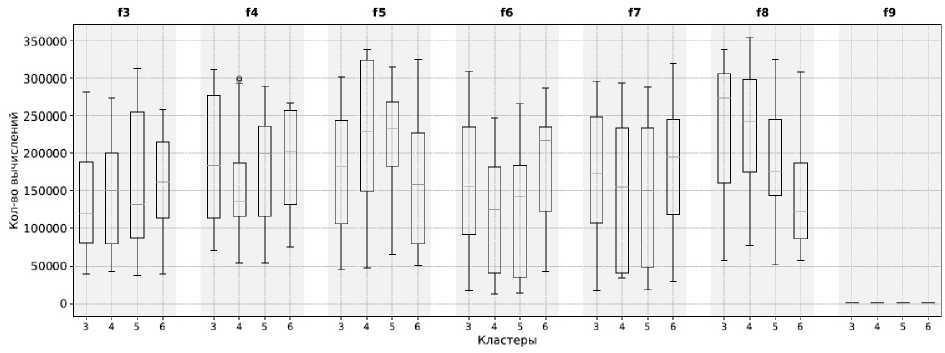
Рис. 6. Диаграммы межквартильного размаха для функций f 3– f 9. Каждый столбик соответствует числу кластеров (3, 4, 5, 6), сгруппированных по функциям. По оси ординат показано количество вычислений целевой функции. Результаты получены с использованием стандартного генетического алгоритма с модификацией, предложенной в настоящей статье

Fig. 6. Boxplot diagrams for functions f 3– f 9. Each bar corresponds to the number of clusters (3, 4, 5, 6), grouped by functions. The y-axis shows the number of objective function evaluations. The results were obtained using the standard genetic algorithm with the modification proposed in this paper

Например, функции f 3– f 8 демонстрируют высокие значения медианы и ширину межквартильного размаха, что указывает на разбросанное потребление вычислительных ресурсов. Вариант алгоритма с модификацией, предложенной в работе, включающей кластеризацию K-means с числом кластеров от 3 до 6, позволил сократить разброс количества вычислений и сместить медиану в сторону меньших значений. Так, генерация индивидов внутри кластеров обеспечивала направленное распределение поиска по пространству решения, что уменьшало количество необходимых вычислений для достижения приближённого оптимума.

Анализ распределения количества вычислений целевой функции для алгоритма SelfCSHAGA (рис. 7 и 8) показывает высокую стабильность и низкую вариативность по сравнению со стандартным ГА.

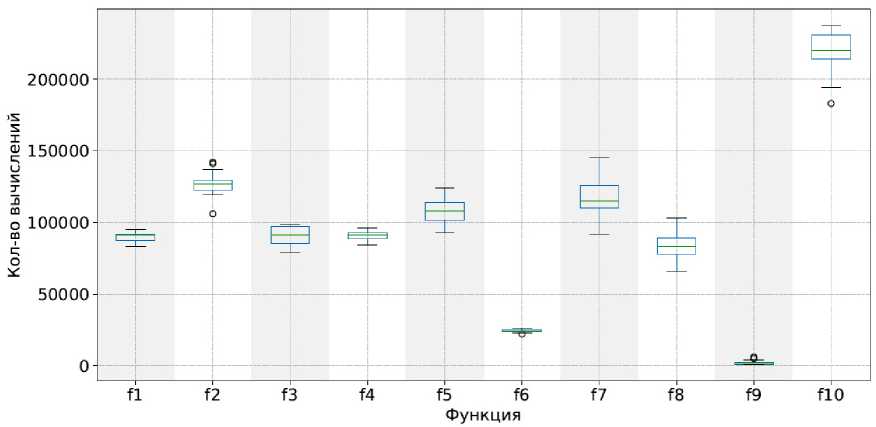
Рис. 7. Диаграммы межквартильного размаха для функций f 1– f 10. По оси ординат показано количество вычислений целевой функции. Результаты получены с использованием алгоритма SelfCSHAGA

Fig. 7. Boxplot diagrams for functions f 1– f 10. The y-axis shows the number of objective function evaluations. The results were obtained using the SelfCSHAGA algorithm

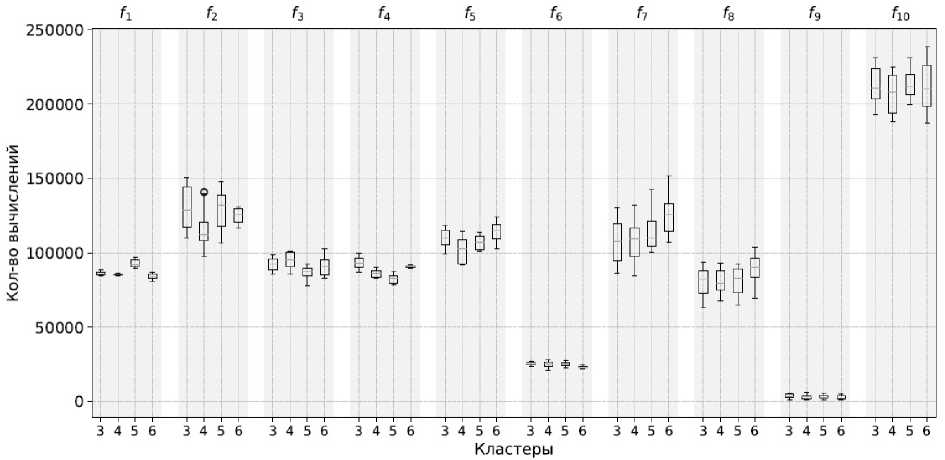
Рис. 8. Диаграммы межквартильного размаха для функций f 1– f 10. Каждый столбик соответствует числу кластеров (3, 4, 5, 6), сгруппированных по функциям. По оси ординат показано количество вычислений целевой функции. Результаты получены с использованием алгоритма SelfCSHAGA с модификацией, предложенной в настоящей статье

Fig. 8. Boxplot diagrams for functions f 1– f 10. Each bar corresponds to the number of clusters (3, 4, 5, 6), grouped by functions. The y-axis shows the number of objective function evaluations. The results were obtained using the SelfCSHAGA algorithm with the modification proposed in this paper

Применение модификации с кластеризацией K-means (число кластеров от 3 до 6) дополнительно снижает разброс вычислений. За счёт распределения популяции по кластерам алгоритм более эффективно исследует пространство решений, особенно на функциях с высокой вычислительной сложностью ( f 3– f 8), уменьшая количество итераций до достижения приближённого оптимума и сужая межквартильный размах. Например, для f 5 и f 7 модифицированный алгоритм потребляет заметно меньше вычислений, чем стандартный SHAGA, при этом IQR сокращается, что отражает более предсказуемую и экономную работу алгоритма.

Заключение

Проведённое исследование предложенного подхода показало, что интеграция метода динамической коррекции области поиска на основе кластеризации в ГА позволяет существенно сократить количество вычислений целевой функции за счёт более точной локализации областей перспективных решений. Коррекция границ областей поиска на основе статистики распределения индивидов в кластерах демонстрирует высокую эффективность в сочетании с динамическим перераспределением вычислительных ресурсов.

Численные эксперименты на репрезентативном множестве тестовых функций подтвердили, что эффективное число кластеров k определяется топологией целевой функции и может варьироваться в широком диапазоне. Небольшие значения k упрощают моделирование ландшафта, но повышают риск пропустить отдельные экстремумы, тогда как избыточно большое k приводит к увеличению количества вычислений. Выбор эффективного значения k (обычно 3–6) обеспечивает наилучший баланс между исследованием пространства решений и использованием результатов исследования, снижая число поколений до сходимости порой в десятки раз по сравнению со стандартным подходом.

Данные результаты подтверждают актуальность и полезность предлагаемого подхода и обосновывают целесообразность дальнейшего его развития. В частности, в дальнейшем целесообразно исследовать возможность автоматической адаптации k в процессе оптимизации, а также расширить список применяемых методов кластеризации за счёт алгоритмов HDBSCAN [21] и самоорганизующихся карт Кохонена [22]. Кроме того, перспективным направлением развития является комбинирование плотностных и графовых подходов для более гибкого управления поисковыми границами в сложных многомерных задачах.