Применение методов машинного обучения в задаче топологической оптимизации упругой пластины

Один из наиболее часто используемых сегодня методов численной оптимизации в механике деформируемого твердого тела - это метод топологической оптимизации. В классической постановке топологическая оптимизация - задача нахождения оптимального с точки зрения жесткости распределения материи в заданной области при определенных нагрузках и граничных условиях. Одним из наиболее быстро развивающихся направлений в области топологической оптимизации является использование методов машинного обучения. Литературный обзор источников позволяет выделить основные цели применения существующих методов машинного обучения в задаче топологической оптимизации: ускорение итерационной процедуры, безытера-ционная оптимизация, метамоделирование, уменьшение размерности пространства проектирования, усовершенствование оптимизатора, генеративный дизайн и постобработка.

В топологической оптимизации, как и в других классических итерационных методах, с увеличением итераций изменение переменных проектирования начинает происходить медленнее. По мере сходимости метода на последних итерациях отклонение переменных проектирования может быть пренебрежительно мало, а время, затрачиваемое на этом этапе, велико. Поэтому часть исследований посвящены использованию нейронных сетей для ускорения итерационной процедуры с помощью предсказания оптимального решения на основе промежуточного, ещё не сошедшегося решения [1-6].

В классическом подходе к топологической оптимизации на каждой итерации вычисление целевой функции, ограничений и их производных по переменным проектирования осуществляется с помощью метода конечных элементов (МКЭ). Метамоделирование предполагает вычисление этих величин с помощью нейронной сети. С помощью сверточной нейронной сети вычисляются податливость, жесткость, объемная доля [7-12]. При этом входными данными для нейронной сети является распределение фиктивной плотности на текущей итерации.

При увеличении размерности модели и ее конечноэлементного разбиения значительно увеличивается время оптимизации за счет большого количество переменных проектирования. В работах [13-24] предлагаются подходы к использованию нейронных сетей для уменьшения количества варьируемых параметров. В частности, в [20; 21] предлагается подход, который использует расширенный вариационный автоэнкодер (VAE) для кодирования 2D-топологий в скрытое пространство параметров меньшего размера и для декодирования выборок из этого пространства обратно в 2D-топологии. Топологическая оптимизация выполняется в скрытом пространстве, а не в пространстве изображений. Другим возможным способом уменьшения количества переменных проектирования является отказ от параметризации с помощью конечно-элементного разбиения и использование геометрических параметров в качестве проектных переменных. Данный подход также демонстрирует высокую эффективность [22–24].

Оптимизированные структуры зачастую имеют низкое качество, поэтому цель многих исследований стоит в том, чтобы повысить его. Нейронные сети в этом случае используются на этапе постобработки результатов оптимизации. Например, в [26–28] генерируется оптимальная структура на грубом КЭ-разбиении и нейронная сеть для повышения качества изображения. В работах [29–30] исследования посвящены постобработке границ сгенерированных изображений с оттенками серого или с нечеткими границами.

Наконец, последняя проблема, которой в последнее время уделяют большое внимание ученые, это полностью безытеративная оптимизация. Данный подход по начальной форме, граничным условиям и нагрузкам дает возможность получить оптимальную топологию конструкции с помощью нейронной сети без проведения оптимизации. Для этого используются сверточные [31–39], генеративно-состязательные [32] и условные генеративно-состязательные сети [33].

В некоторых работах авторы для обобщения этого подхода на различные граничные условия дополняют входной массив полем перемещений [34], деформаций [35] или главными напряжениями [36]. В работе [37] предложена условная генеративно-состязательная сеть (cGAN-type), на вход которой дополнительно передается плотность энергии деформации и эквивалентные по Мизесу напряжения, полученные из МКЭ.

В настоящей работе предлагается подход по использованию нейронной сети именно для безытераци-онной топологической оптимизации. Основным его отличием от предложенных ранее и описанных в литературе подходов является использование не стандартных общепринятых слоев нейронной сети, а разработка собственной высокоэффективной структуры нейронной сети, основанной на наблюдениях за характером поведения параметров проектирования в зависимости от входных параметров.

1.    Топологическая оптимизация в механике деформируемого твердого тела

Задача топологической оптимизации в механике деформируемого твердого тела представляет собой поиск минимума некоторого функционала в пространстве проектирования при заданных граничных условиях и нагрузках. При оптимизации жесткости тела в качестве целевой функции выступает упругая энергия деформации пространства проектирования, имеющая следующий вид:

с =—К4 C ■■£)■■£ dQ ^ min, (1) 2Ω где 4C – тензор упругих коэффициентов, ε – тензор деформаций, Ω – материальный объём (пространство проектирования).

Параметризация пространства оптимизации выполняется за счет конечно-элементной дискретизации и применения SIMP (Solid Isotropic Material with Penalization) подхода. Свойства материала постоянны в каждом элементе и зависят величины фиктивной плотности р _e , называемой фиктивной плотностью. Значения фиктивной плотности изменяются от 0 до 1, предполагается, что:

⁴ C e = Р Р 4 C e 0 ,                       (2)

где ⁴ C_{e 0} – изначальный тензор упругих коэффициентов в данном конечном элементе, р – штрафной фактор.

В качестве ограничения выступает максимально разрешенный процент использования объема пространства проектирования, выраженный следующим неравенством:

J p ( r ) d Q <  V .                    (3)

Ω

Таким образом, задача нахождения распределения материала в рассматриваемой области проектирования в конечно-элементной постановке выглядит следующим образом:

min C (p) = fT u, ρe при ограничениях:

[ Ku = f

Ne

^eV e <  V               (4)

e

_ 0

Здесь C ( p ) - податливость конструкции; p - вектор проектных переменных; u – вектор узловых перемещений; f – вектор узловых нагрузок; K – матрица жесткости конструкции; N_e – количество конечных элементов; р e - фиктивная плотность e -го элемента; V_e – объем элемента; V – целевой объем;

Для решения этой задачи далее применяются методы математического программирования, в частности метод скользящих асимптот. В данной работе с помощью метода скользящих асимптот (Method of moving asymptotes – MMA) генерируется набор данных для обучения нейронной сети, и далее рассматривается возможность получения решения уже непосредственно с помощью самой нейронной сети.

2.    Искусственная нейронная сеть

Искусственные нейронные сети представляют собой вычислительные модели, построенные на эмуляции процессов в нейронных структурах человеческого мозга. Классическая архитектура многослойной нейронной сети имеет входной и выходной слои. Промежуточные слои, заключенные между входным и выходным слоями, называются скрытыми. Каждый слой содержит конечное количество нейронов, в пределах одного слоя они не сообщаются между собой, но имеют связь с нейронами, принадлежащим соседним слоям. Нейрон вычисляет взвешенную сумму входных сигналов вместе с коэффициентом смещения и подает на вход в качестве аргумента нелинейной функции – функции активации. Полученное значение данной функции передается на вход нейронам, принадлежащим следующему слою.

Наиболее эффективным методом обучения многослойных нейронных сетей является метод обратного распространения ошибки. Метод обратного распространения ошибки подразумевает прямой и обратный проходы по слоям нейронной сети. Во время прямого прохода входной вектор подается на входной слой нейронной сети и передается последующим, при этом весовые коэффициенты остаются постоянными. Во время обратного прохода происходит настройка весовых коэффициентов с целью минимального расхождения прогнозируемых и фактических значений выхода. Корректировка весов осуществляется по дельтаправилу, обновленные значения весов вычисляются по следующей формуле:

wkj( n+1)=wj n ^lE-, (5) d wj где X - параметр скорости обучения, E - функция ошибки.

Качество обучения нейронной сети будет оцениваться по суммарной квадратичной ошибки, которая определяется как сумма квадратов разностей истинного и полученного значений.

1 ^N 1 ^N 2

^E = 2 Е ^ej = 2 Е ( ^dj ^- л ) . ⁽⁶⁾

3.    Подготовка тренировочных и тестовых данных

Для демонстрации работы данного метода рассматривается изотропная квадратная упругая пластина со стороной размером 1 см. Одна из ее граней жестко закреплена, к другой грани приложена сила F = 1 кН, как показано рис. 1. Материал пластины обладает следующими характеристиками: модуль упругости E = 0,1603 МПа, коэффициент Пуассона v = 0,32.

Тренировочные данные получаются с помощью решения задачи минимизации податливости при ограничении на объёмную долю в 30 %. При этом меняется положение нагрузки вдоль правой кромки. Всего получено 30 топологий для разных точек приложения нагрузки. Для решения задачи топологической оптимизации используется метод конечных элементов (ANSYS) и метод скользящих асимптот (DS Simulia

Tosca Structure). Таким образом, формируется набор данных, состоящий из вектора, содержащего координаты силы, и матрицы, имеющей двоичное представление. Номера строк матрицы соответствуют различным точкам приложения силы, а номера столбцов – номерам элементов. Единичное значение элемента матрицы предполагает наличие структурного элемента, нулевое значение – его отсутствие.

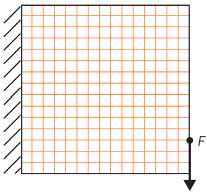
Рис. 1 Рассматриваемая геометрия

Fig. 1. 2D design domain and boundary conditions

4.    Структура нейронных сетей

В данном разделе представлены архитектуры двух нейронных сетей для предсказания оптимальной топологии по заданной нагрузке на основе тренировочных данных, полученных в предыдущем пункте.

На выходе нейронной сети каждому элементу присваивается либо «0», либо «1» в зависимости от факта наличия материала в элементе. Исходя из этого, область значений аппроксимирующей функции должна быть в пределах отрезка [0;1]. При изменении положения точки приложения силы, оптимальная топология пластины меняется непрерывно, «отслеживая» положение приложенной нагрузки. Таким образом, в оптимальной конструкции выбранному конечному элементу в определенных положениях нагрузки будет соответствовать значение «1», во всех остальных положениях – «0». Значит на графике функции плотности конечного элемента в зависимости от координаты приложенной нагрузки должны наблюдаться плато, также функция должна быть способна к резкой смене монотонности

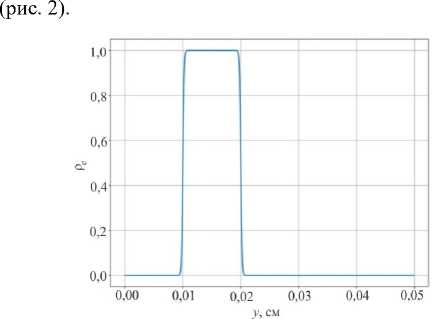
Рис. 2. Зависимость плотности в конечном элементе от положения нагрузки

Fig. 2. Element density-force coordinate graph

Данным критериям удовлетворяет сигмоида и ступенчатая функция. Но ступенчатая функция претерпевает разрыв, следовательно, она не дифференцируема во всех точках. Также ступенчатая функция имеет нулевые производные, что приводит к невозможности ее использования в методе обратного распространения, поэтому необходимо использовать ее гладкие аналоги. Для ее реализации необходимо сложить две сигмоиды с противоположными знаками, причем сигмоида с отрицательным знаком должна находиться всегда правее. Для данной задачи в силу наличия нескольких плато предлагается следующая функция:

f ⁽ y ) i + e - a ⁽ y - b )

1 + e - a ⁽ y ^- b ^- c )

+--; ;---;-----r, (7)

1 + e ^- a ⁽ у ^- n ) 1 + e ^- a ⁽ у ^- n ^- t )

где a – коэффициент, отвечающий за скорость роста экспоненциальных сигмоид, b и n – параметры нейронной сети, отвечающие за смещение «ступенек», c и t – заведомо положительные параметры нейронной сети, отвечающие за ширину «ступенек»

Во время аппроксимации функцией f (y) коэффициент a не будет варьироваться. Для минимизации ошибки и наилучшей аппроксимации ступенчатой функцией требуется присвоить этому параметру достаточно большое значение.

Представленная нейронная сеть на рис. 3 содержит один нелинейный слой.

Структура второй нейронной сети изображена на рис. 4. Данная модель содержит два полносвязанных скрытых слоя и выходной слой.

Функцией активацией для скрытых слоев служит функция ReLu (рис. 5), а для выходного слоя для получения значений в пределах от 0 до 1 – экспоненциальная сигмоида (рис. 6).

На выходе полученных нейронных сетей будут представлены предсказанные вероятности нахождения элементов в зависимости от координаты приложения силы. Для получения наглядного представления данные числа округляются.

Рис. 3. Схема первой нейронной сети

Fig. 3. The architecture of single-layer neural network

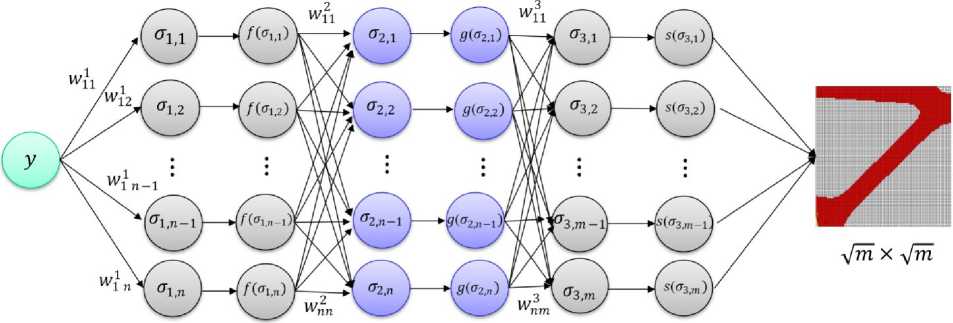
Рис. 4. Архитектура многослойной нейронной сети

Fig. 4. The architecture of multilayer neural network

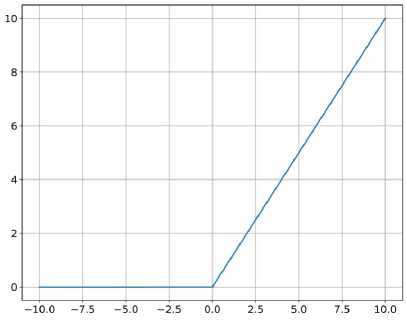
Рис. 5 ReLu

• Fig. 5.    ReLU function

5.    Анализ результатов

Точность прогнозирования нейронной сети определяется по средней ошибке:

E av = ^E ,                        (8)

n где E – суммарная среднеквадратичная ошибка по обучающей выборке, определяемая по формуле (6), n – размер обучающей выборки.

Средняя ошибка для двух разработанных нейронных сетей, полученная в результате их обучения на указанных в п.3. тренировочных данных, приведена в табл. 1.

Таблица 1

Средняя ошибка нейронной сети

Table 1

Neural network average error

Нейронная сеть	Средняя ошибка	Доля элементов с ошибкой ( N err / N e )
Однослойная	29,85	0,00597
Трехслойная	10,4	0,00208

В последнем столбце N err – среднее количество элементов с ошибкой, N e – общее количество конечных элементов.

Интерпретировать величину средней ошибки можно следующим образом – ошибка, равная N , означает, в соответствии с формулой (6), что в среднем 2 N элементов имеют конечную плотность «1» вместо «0» (или наоборот). Таким образом, величина ошибки указывает на количество элементов c ошибочной плотностью в конечной топологии. Для оценки качества работы

Рис. 6. Сигмоидальная функция

• Fig. 6.    Sigmoid function

нейронной сети это количество должно быть соотнесено с общим количеством элементов (столбец 2 табл. 1). Таким образом, однослойная нейронная сеть неправильно определяет в среднем 60 из 10 000 элементов конечноэлементной модели, а трехслойная – 20 из 10 000. Влияние данной ошибки на результаты можно увидеть на рис. 7–9, на которых показаны результаты прогноза однослойной и трехслойной нейронных сетей и сравнение этих прогнозов с решением, полученным с помощью оптимизации методом MMA. На рис. 7 приведены результаты для случая приложения нагрузки в верхней части правой кромки пластины, на рис. 8 – для случая приложения нагрузки ближе к центру кромки, на рис. 9 – для случая приложения нагрузки в нижней части кромки.

На рис. 7, а , показаны неточности вдоль верхней кромки нижнего «ребра», а на рис. 9, b , относящемуся к трехслойной нейронной сети, можно увидеть ошибку в виде нулевой плотности в элементе, расположенном на стыке двух «ребер». Эти ошибки, однако, не оказывают существенного влияния на конечную топологию и могут быть нивелированы как за счет введения дополнительных фильтров, так и за счет применения генеративно-состязательной нейронной сети, которая сможет воссоздать «изображение» без дефектов по заданному «изображению» с дефектами. Создание такое нейронной сети – одно из возможных направлений для продолжения исследований по данной теме.

Время, затраченное на получение оптимальной топологии с помощью нейросети, приведено в табл. 2. Данная таблица не включает время, затраченное на создание тренировочной выборки и обучение сети. Время обучения для однослойной нейронной сети составило 21,7 мин, а для трехслойной – 41 мин. На создание обучающей выборки было затрачено примерно 3 ч 43 мин.

Рис. 7. Оптимальная топология для силы, приложенной в точке с координатой y = 0,805: а – прогноз однослойной нейронной сети; b – прогноз многослойной нейронной сети; c – результат оптимизации с помощью MMA

Fig. 7. Optimized designs with force applied at y = 0.805: a – prediction result of single-layer neural network; b – prediction result of multilayer neural network; c – result of MMA method

а                                           b                                           c

Рис. 8. Оптимальная топология для силы, приложенной в точке с координатой y = 0,625: а – прогноз однослойной нейронной сети; b – прогноз многослойной нейронной сети; c – результат оптимизации с помощью MMA

Fig. 8. Optimized designs with force applied at y = 0,625: a – prediction result of single-layer neural network; b – prediction result of multilayer neural network; c – result of MMA method

а                                            b                                           c

Рис. 9. Оптимальная топология для силы, приложенной в точке с координатой y = 0,185: а – прогноз однослойной нейронной сети; b – прогноз многослойной нейронной сети; с – результат оптимизации с помощью MMA

Fig. 9. Optimized designs with force applied at y = 0,185: a – prediction result of single-layer neural network; b – prediction result of multilayer neural network; c – result of MMA method

Таблица 2

Сравнение времени, требуемого на решение задачи оптимизации

Comparison of the time required to solve the optimization problem

Table 2

Параметр	Однослойная нейронная сеть	Трехслойная нейронная сеть	Оптимизация с помощью MMA
Время решения задачи оптимизации, с	0,24	0,16	120
Занимаемая оперативная память, МБ	23	29	788

Видно, что обе нейронные сети испытывают небольшие трудности при определении значений на границе модели. Поэтому, как и в обычных задачах топологической оптимизации, требуется небольшая постобработка сторонними средствами. Вторая нейронная сеть в среднем более точное решение, что неудивительно в силу более большого количества параметров.

В силу нелинейности аппроксимирующей функции в первой нейронной сети, а также наличия у нее нескольких локальных экстремумов, конечная топология зависит от начальных параметром сигмоид, однако примерную топологию возможно получить и со случайными ненулевыми параметрами. Также преимуществом этой сети является малое количество параметров по сравнению с многослойными сетями, без существенных потерь в результативности.

Заключение

В данной работе представлены две структуры нейронных сетей для безытерационого решения задачи топологической оптимизации в постановке минимизации податливости с ограничением на объем. Первая структура нейронной сети содержит один нелинейный слой, вторая структура представляет собой трехслойную нейронную сеть. Разработанные модели прекрасно