Применение методов математического программирования для градуировки БИК-анализаторов

На сегодняшний день во многих отраслях промышленности, в том числе и в сельском хозяйстве, одной из главных задач является исследование состава продукции. Подобные данные просто необходимы для оптимизации технологического процесса (сокращение расхода сырья, повышение качества продукции), определения стоимости продукции, идентификации и обнаружения фальсификации образцов. Для решения данной задачи в настоящее время все чаще используют методы, основанные на спектральном анализе в ближней инфракрасной (БИК) области [1].

Преимущества метода БИК-анализа в том, что он занимает значительно меньше времени и не требует применения дополнительных реактивов, высокой квалификации персонала и хорошо оборудованных лабораторий, как в случае с методами химического анализа. Анализ проводится с помощью специальных приборов, удобных в эксплуатации и позволяющих в короткие сроки получить необходимые результаты с достаточно высокой точностью.

Однако, прежде чем использовать анализатор, его необходимо предварительно отградуировать, чтобы найти взаимосвязь между содержанием анализируемых компонентов и спектральными характеристиками. Для этого отбираются градуировочный и валидационный (проверочный) наборы образцов с известными референтными значениями, а также регистрируются их спектральные данные. Референтные значения градуировочного и валидационного наборов — это анализируемые параметры образцов, которые определяются при помощи независимых референтных методов, имеющих заданную точность и воспроизводи- мость. Величины, измеряемые непосредственно анализатором, называются спектральными данными. Диапазон изменения референтных значений образцов должен полностью охватывать диапазон возможных изменений этих значений при последующем анализе неизвестных образцов. Кроме того, для создания наиболее устойчивой модели образцы в градуировочном наборе должны быть однородно распределены в диапазоне изменения анализируемых свойств, а также количество вали-дационных образцов должно быть не меньше 50 [2]. Таким образом, формируются матрица X спектральных данных градуировочного набора размерности n х f (n — количество образцов в градуировочном наборе, а f — число точек спектра) и матрица Y референтных значений градуировочного набора размерности n х k (к — количество исследуемых компонентов). Матрицы X' и Y' валидационного набора отличаются от градуировочного меньшим количеством образцов.

Известно, что в БИК-спектроскопии используемые количественные связи зачастую слишком сложны, т. к. спектры в БИК-области содержат множество широких перекрывающихся полос поглощения (отражения, рассеивания), которые накладываются на полосу интересующего компонента. Это не позволяет построить простую градуировочную зависимость между интенсивностями характерной полосы с содержанием интересующего вещества. В таком случае формируют многомерную градуировочную модель (MVC — multivariate calibration), которая связывает весь массив спектральной информации с содержанием интересующего компонента.

Наиболее часто для создания MVC используют метод проекции на латентные структуры (PLS — partial least squares) и метод регрессии на главных компонентах (PCR — principial component regression) [3]. PCR — довольно простой метод, требующий меньше вычислительной мощности, чем PLS, его используют для хорошо изученных наборов, где построение MVC с удовлетворяющими характеристиками не вызывает особых трудностей. PLS создан на основе PCR и существенно расширяет его возможности. Метод хорошо работает, когда в спектральных данных существует сильная корреляция или имеется набор спектральных данных, число столбцов в котором сильно превышает число строк [4]. Однако при наличии сложных связей в спектральных данных или отсутствии ярко выраженных особенностей для создания лучшей MVC возможности обоих методов весьма ограничены за счет удаления латентных переменных высших порядков.

Нейронные сети все больше набирают популярность в задачах создания MVC. Тем не менее наряду с преимуществами они имеют два основных недостатка. Их архитектура должна быть определена заранее, т. к. изменение ее в процессе обучения довольно сложная задача. Второй недостаток в том, что нейронные сети могут застревать в локальных минимумах во время обучения, а во многих случаях это нежелательно [5].

Таким образом, поиск более выгодной альтернативы в создании MVC для решения конкретных задач, где общие методы слабы, является актуальной задачей. В качестве такой альтернативы можно предложить технику математического программирования (МП), которая успешно используется в подобных задачах построения MVC [6].

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Математическое программирование в задачах многомерной градуировки

Математическое программирование — это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, МП занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных.

Хотя градуировочные характеристики могут описываться самыми разными функциями, считается вполне достаточным ограничиться случаем линейной зависимости. Это обусловлено тем, что разработчики методик чаще всего сводят градуировку к нахождению линейной зависимости. Другими словами, мы будем полагать, что величины X и Y связаны линейной зависимостью, а задачу градуировки анализатора можно записать в виде

Y = Xb + e , (1)

где b — вектор регрессионных коэффициентов, e — вектор, содержащий значения ошибки. Следовательно, градуировка спектрометра заключается в подборе таких регрессионных коэффициентов b , чтобы квадрат ошибки f был минимален. Таким образом, целевую функцию для задачи оптимизации можно представить следующим образом:

f = ( Y - Xb )^T( Y - Xb ), (2)

где f — вектор ( f ₁, f ₂,..., f_n ), содержащий квадраты указанной выше ошибки e . Если ввести ограничения на область поиска экстремальных значений целевой функции, коэффициенты регрессии b должны находиться внутри пространства гиперкуба, где гиперкуб — это фигура в евклидовом пространстве E _n ( n — размерность пространства). Например, если n = 3, то гиперкуб — это куб в трехмерном евклидовом пространстве, имеющий длину ребра, равную d . Целевую функцию (2) можно представить в виде задачи квадратичного программирования:

f = ( Y - Xb )^T( Y - Xb ) 0 . , — d > min. (3)

Для удобства записи введем следующие переменные:

C = 2( X T • X ); (4) D = - 2( X ^T • Y ).

Тогда задача (3) может быть представлена в виде классической задачи квадратичного программирования:

f ( x ) = D ^T b + b ^T Cb — ₀ < _{b <} d >  min, (5)

где b — искомый вектор ( b ₁, b ₂,..., b_n ), вектор d ( d ₁, d ₂,..., d_n ), представляет указанное выше пространство ограничений. Оптимальное значение параметра d определяется с помощью процедуры валидации, что подразумевает конечную проверку созданной модели и изменение размерности гиперкуба до тех пор, пока критерии оценки качества градуировочной модели не будут удовлетворять необходимым условиям.

Данную задачу можно решить с помощью искусственного базиса и симплекс-метода. Однако у такого подхода есть ряд недостатков, например, если C будет положительно полуопределенной матрицей, то данный метод будет расходиться. Существует более простой и эффективный метод решения подобной задачи, называемый методом решения задачи о дополнительности. Для того чтобы представить задачу квадратичного программирования в виде задачи о дополнительно- сти, существует специальная методика, подразумевающая выполнения следующих операций [7].

Для начала записывается функция Лагранжа для данной задачи квадратичного программирования (5):

L ( u , v ) = f ( x ) - u ^T b - v ^T ( d - b ) .          (6)

На основании (6) можно записать условия Куна— Таккера для данной задачи квадратичного программирования (5):

V f - u - v = 0;

u ^T b = 0 ; v ^T ( d - b ) = 0;

d - b >  0;

u , v >  0.

Затем, для того чтобы заменить ограничение-неравенство ограничением-равенством, предполагается введение дополнительного вектора S . Причем d - b - S = 0, и благодаря этой подстановке условия Куна—Таккера (7) представляются следующим образом:

V f - u - v = 0;

u ^T b = 0 ; v ^T S = 0;             (8)

S >  0 ; u , v >  0.

На последнем шаге для системы, записанной в (8), делаются следующие замены:

M =

Г 2 Q

z =

q =

Г D T

x ^d

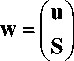
b

| .

I y )

Задача (5) принимает вид эквивалентной задачи о дополнительности:

w = Mz + q ;

w >  0 ; z >  0; w ^T z = 0.

Решив данную систему, получим вектор коэффициентов z , который и будет оптимальным вектором регрессионных коэффициентов b для целевой функции задачи построения MVC-анализатора, записанной в уравнении (2).

Таким образом, при исследовании образца с неизвестной концентрацией интересующего компонента у производится регистрация спектра X0 на анализаторе, а затем с помощью выражения y = XT • b (11)

можно оценить значение у .

Критерии для оценки качества градуировочной модели

Для оценки качества градуировочной зависимости была использована статистическая характеристика, широко применяющаяся в зарубежной практике, — SEV (Standard Error of Validation), стандартная ошибка валидации [8].

SEV характеризует ошибку отклонения между референтными и предсказанными по градуировочному уравнению значениями для образцов дополнительного набора (т. е. серии образцов, не входивших в градуировочный набор и используемых для проверки градуировки):

v

SEV = a Z ( У - - У - ) ²/ ^d v ,         (12)

V ,=i dv — число образцов дополнительного набора; у, — референтное значение анализируемого компонента для i -го образца дополнительного набора; у, — предсказанное по градуировочному уравнению значение анализируемого компонента для i -го образца дополнительного набора.

ЭКСПЕРЕМЕНТАЛЬНАЯ ЧАСТЬ

В наших экспериментах мы сравнивали метод создания MVC с помощью техники МП с известными классическими методами — PLS и PCR.

Наборы данных и оборудование для создания многомерной градуировочной модели

Предлагаемый способ создания MVC для градуировки БИК-анализаторов оценивался на трех различных наборах данных. Для измерения спектральных данных был выбран БИК-анализатор "ИНФРАЛЮМ ФТ-10" — современный анализатор, выпускаемый компанией "Люмэкс". Спектры образцов измерялись в диапазоне волновых чисел 8 000–14 000 см–1 с разрешением 16 см–1.

Первый набор — образцы зерен кукурузы с известными референтными данными процентного содержания жира. Градуировочный набор содержит 67 образцов, валидационный набор — 10 образцов.

Второй набор — образцы шрота подсолнечника с известными референтными данными процентного содержания протеина. Градуировочный набор содержит 74 образца, валидационный набор — 10 образцов.

Третий набор — образцы комбикормов с известными референтными данными процентного содержания кальция. Градуировочный набор содержит 53 образца, валидационный набор — 10 образцов.

Результаты приведены в табл. 1–3.

Табл. 1. Результаты предсказания массовой доли жира в зернах кукурузы для образцов валидационно-го набора по градуировочным моделям, построенным различными способами

Образец	Реф. значение	Метод построения многомерной градуировочной модели
		PCR	PLS	МП
kuk-0350	5.04	4.59	4.42	4.85
kuk-0327	7.99	6.60	7.05	6.75
kuk-0259	6.79	5.92	6.16	6.59
kuk-0288	7.70	7.32	7.25	6.88
kuk-0322	3.41	4.74	4.59	4.07
kuk-0232	6.29	6.30	6.63	6.18
kuk-0248	4.50	5.21	4.79	4.42
kuk-0375	4.28	5.31	4.84	4.30
kuk-0307	3.27	5.42	5.07	3.32
kuk-0246	5.70	5.20	5.05	5.32
Значение SEV		1.19	0.99	0.62

Табл. 2. Результаты предсказания массовой доли протеина в шроте подсолнечника для образцов валидационного набора по градуировочным моделям, построенным различными способами

Образец	Реф. значение	Метод построения многомерной градуировочной модели
		PCR	PLS	МП
chm-1141	43.99	40.51	43.02	43.54
chm-1152	44.04	42.45	43.04	43.43
chm-1145	42.58	41.03	42.82	42.77
chm-1266	38.90	38.75	38.78	38.44
chm-1133	40.26	39.02	40.22	40.44
chm-1280	41.80	38.92	40.22	41.01
chm-1118	36.79	37.18	37.80	37.57
chm-1119	37.09	38.41	39.28	38.46
chm-1219	35.57	37.69	36.20	35.11
chm-1126	39.97	39.19	40.19	40.38
Значение SEV		1.99	1.25	0.91

Это позволяет сделать вывод о том, что техника математического программирования может применяться в качестве метода для поиска регрессионных коэффициентов в задачах построения MVC, и в частности для градуировки БИКанализаторов. Методы математического программирования в определенных случаях позволяют создавать градуировки, обеспечивающие более высокую точность, чем градуировки, полученные с помощью классических методов.