Применение методов математической статистики для оценки инвестиционного потенциала региона
Автор: Болодурина И.П., Болодурина М.П., Абельгазина К.М.
Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet
Рубрика: Экономика и управление
Статья в выпуске: 1 (91), 2022 года.
Бесплатный доступ
Поскольку каждый субъект Российской Федерации обладает полными правами на ведение как межрегиональных, так и международных экономических отношений, то показатели регионального развития во многом зависят от реализуемой инвестиционной стратегии, в том числе от уровня инвестиционного потенциала. В этой связи в статье рассматривается актуальная задача оценки инвестиционного потенциала региона на основе социально-экономических показателей методами математической статистики, что позволяет получить объективные и достоверные результаты, а также обеспечивает масштабируемость используемой методики и возможность ее применения для анализа инвестиционного потенциала других регионов Российской Федерации. Использованы корреляционно-регрессионный анализ, проведено исследование линейной регрессионной модели на мультиколлинеарность. Применение многомерного статистического анализа показателей инвестиционной привлекательности Оренбургской области позволило выявить наиболее значимые факторы, оказывающие влияние на объем инвестиций в основной капитал региона, к которым относятся: объем работ, выполненных по виду экономической деятельности «Строительство»; среднедушевые денежные доходы населения; объем продукции обрабатывающего производства; удельный вес численность населения в трудоспособном возрасте в общей численности. На основании результатов корреляционно-регрессионного анализа сделан вывод о том, что на уровень объема инвестиций в основной капитал Оренбургской области наиболее значимое влияние оказывают такие сферы экономической деятельности, как сельское хозяйство, добыча полезных ископаемых и обрабатывающие производства. Привлечение инвестиций в выявленные отраслевые приоритеты инвестиционной привлекательности Оренбургской области обеспечит создание высокопроизводительных мест на территории региона, увеличение валового регионального продукта, а также даст мультипликативный эффект для развития других видов деятельности.
Инвестиционный потенциал, корреляционно-регрессионный анализ, инвестиционная привлекательность, математическая статистика
Короткий адрес: https://sciup.org/140293775
IDR: 140293775 | УДК: 311.1:311.313
Текст научной статьи Применение методов математической статистики для оценки инвестиционного потенциала региона
Инвестиционная активность экономического субъекта во многом определяет вектор его экономического развития. Для грамотного построения приоритетов формирования основных направлений социально-экономического развития субъекта Российской Федерации необходимо вести учет особенностей его географического расположения, развития отраслей экономики, ресурсов труда, наличия месторождений природных ресурсов и других компонентов инвестиционного потенциала. Современное состояние информационной среды позволяет использовать большое количество данных и показателей для подготовки и обоснования управленческих решений инвестиционного характера. Применение методов математической статистики позволяет повысить объективность, как используемых данных, так и полученных результатов.
This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License
Материалы и методы
Подробный анализ существующих зарубежных и отечественных методик оценки инвестиционной привлекательности регионов проведен в статье Кособуцкой А.Ю. и Равунжинириной А.В., авторами отмечается большое разнообразие используемых показателей оценки и варьируемо-сти параметров в зависимости от целей оценки, а также в методах обработки информации и оценке результатов [1]. Множественность используемых параметров оценки инвестиционного потенциала территории отмечается и в зарубежных исследованиях [13, 14, 16].
Интеграционный подход и возможности его применения для оценки частных и общего инвестиционного потенциала региона представлены в трудах Болодуриной М.П. и Мишу-ровой А.И. [3, 15]. Авторы перечисленных выше исследований наряду с субъективными критериями оценки инвестиционного потенциала региона используют показатели национального рейтинга состояния инвестиционного климата в субъектах РФ [2, 8], аналитические данные рейтинговых агентств [4, 9], а также данные официальной статистики.
Статистические методы анализа в оценке инвестиционного потенциала региона применялись в работах Валерианова А.А. и его соавторов [5], Дмитриева Н.Д. [6] и других отечественных авторов. Экономико-математическое моделирование лежит в основе и многих зарубежных исследований, Куммел Р., Хенн Дж. И Линденбергер Д проводят моделирование распространения инвестиций и инноваций в зависимости от таких параметров как капитал, труд, энергия и креативность [16]. Результаты кластерного анализа при разработке инвестиционных рекомендаций представлены в трудах Лео В., Донгхун С. И других [20, 21].
Таким образом, затруднение вызывает не недостаток, а наоборот многочисленность, используемых данных и методик их оценки. Оценка инвестиционного потенциала региона на основе социально-экономических показателей методами математической статистики позволит повысить достоверность объективность получаемых оценок и объективность сделанных на их основе выводов.
В настоящем исследовании для проведения многомерного статистического анализа показателей инвестиционной привлекательности Оренбургской области на основании статистических данных за одиннадцатилетний период [7], представленных в таблице 1 проведен корреляционный анализ социально-экономических показателей, характеризующих инвестиционную привлекательность региона.
В качестве исходных показателей использованы следующие:
ξ 1 – инвестиции в основной капитал
(млн рублей);
ξ 2 – объем работ, выполненных по виду экономической деятельности «Строительство» (млн рублей);
ξ 3 – среднедушевые денежные доходы населения (в месяц рублей);
ξ 4 – оборот розничной торговли (млн рублей);
ξ 5 – уровень добычи полезных ископаемых (в фактически действовавших ценах; млн рублей);
ξ 6 – объем продукции обрабатывающего производства (в фактически действовавших ценах; млн рублей);
ξ 7 – продукция сельского хозяйства
(млн рублей);
ξ 8 – удельный вес численности населения в трудоспособном возрасте в общей численности (проценты);
ξ 9 – объем инновационных товаров, работ, услуг (млн рублей);
ξ 10 – валовой региональный продукт
(в основных ценах, млн рублей).
Таблица 1.
Исходные выборочные данные
Table 1.
Initial sample data
|
Год Year |
Показатель | Indicator |
|||||||||
|
ξ 1 |
ξ 2 |
ξ 3 |
ξ 4 |
ξ 5 |
ξ 6 |
ξ 7 |
ξ 8 |
ξ 9 |
ξ 10 |
|
|
2009 |
91268,0 |
25826,3 |
12008,1 |
136473,4 |
185875,0 |
117413,0 |
55288,3 |
63,4 |
6914,0 |
413395,5 |
|
2010 |
103648,0 |
31409,1 |
13557,1 |
157681,8 |
215311,0 |
151634,0 |
47707,8 |
63,6 |
11651,4 |
458145,4 |
|
2011 |
116658,0 |
35025,4 |
14892,0 |
187098,8 |
282235,0 |
174977,0 |
69144,2 |
60,6 |
14230,1 |
553320,9 |
|
2012 |
151250,0 |
41873,5 |
16541,9 |
214089,8 |
313118,0 |
211629,0 |
68019,0 |
63,7 |
9244,6 |
628563,6 |
|
2013 |
152877,0 |
41456,1 |
18389,9 |
240773,4 |
420880,0 |
192004,0 |
77641,4 |
63,4 |
8870,3 |
717014,8 |
|
2014 |
153979,0 |
47597,4 |
20699,9 |
269615,0 |
348081,0 |
230679,0 |
83840,4 |
60,4 |
6888,9 |
731277,7 |
|
2015 |
169243,0 |
60566,7 |
22943,1 |
278368,2 |
383955,0 |
274498,0 |
99108,4 |
62,5 |
14671,4 |
774962,1 |
|
2016 |
167278,5 |
49750,8 |
22144,8 |
274944,3 |
338587,0 |
274312,0 |
110753,6 |
61,9 |
25264,1 |
765333,3 |
|
2017 |
184877,2 |
62949,9 |
22909,8 |
293997,0 |
389692,4 |
304238,0 |
113038,3 |
60,0 |
23250,7 |
823856,4 |
|
2018 |
208105,1 |
78643,5 |
23384,8 |
307946,0 |
527943,1 |
348347,7 |
107971,1 |
61,0 |
28408,6 |
1058504,8 |
|
2019 |
211726,5 |
100988,0 |
24482,7 |
327692,6 |
561650,8 |
315272,8 |
113015,9 |
60,2 |
41663,7 |
1107155,3 |
Данный выбор обусловлен проведенным анализом работ по оценке инвестиционной привлекательности регионов РФ, в результате которого выявлены наиболее часто встречающиеся социально-экономические показатели, оказывающие влияние на уровень инвестиционной привлекательности. Кроме того, для исследования выбраны показатели, в наибольшей мере характеризующие экономическую деятельность Оренбургской области.
Точечное оценивание параметров многомерного вектора признаков сводится к оценке вектора математических ожиданий и ковариационной матрицы в виде вектора средних значений и выборочной ковариационной матрицы. С помощью пакета Statistica рассчитаны значения выборочных средних, дисперсий и средних квадратических отклонений для каждого рассматриваемого признака. Полученные результаты представлены в таблице 2. Для получения выборочной ковариационной матрицы использован табличный редактор MS Excel (надстройка «Пакет анализа») [10].
Таблица 2.
Описательная статистика исследуемых признаков
Table 2.
Descriptive statistics of the studied features
|
Показатель Indicator |
Mean |
Variance |
Std. Dev. |
|
ξ 1 |
155537,3 |
1546966030 |
39331,5 |
|
ξ 2 |
52371,5 |
493681701 |
22218,9 |
|
ξ 3 |
19268,6 |
19390910,2 |
4403,5 |
|
ξ 4 |
244425,5 |
3954168087 |
62882,2 |
|
ξ 5 |
360666,2 |
13412522147 |
115812,4 |
|
ξ 6 |
235909,5 |
5397463417 |
73467,4 |
|
ξ 7 |
85957,1 |
581967392 |
24124,0 |
|
ξ 8 |
61,9 |
2,18274182 |
1,5 |
|
ξ 9 |
17368,9 |
121622620 |
11028,3 |
|
ξ 10 |
730139,1 |
47805879605 |
218645,6 |
Всего рассматривается 45 связей, из них 36 характеризуются прямой связью, а 9 – обратной. В пакете Statistica рассчитаны выборочные значения коэффициентов корреляции для каждой пары признаков. Таким образом, в результате расчетов получена оценка корреляционной матрицы вида:
|
( 1 |
0,92 |
0,95 |
0,97 |
0,94 |
|
|
0,92 |
1 |
0,86 |
0,88 |
0,92 |
|
|
0,95 |
0,86 |
1 |
0,99 |
0,86 |
|
|
0,97 |
0,88 |
0,99 |
1 |
0,90 |
|
|
R k = |
0,94 |
0,92 |
0,86 |
0,90 |
1 |
|
0,97 |
0,89 |
0,95 |
0,95 |
0,86 |
|
|
0,91 |
0,82 |
0,96 |
0,94 |
0,80 |
|
|
- 0,57 |
- 0,61 |
- 0,62 |
- 0,65 |
- 0,54 |
|
|
0,77 |
0,89 |
0,71 |
0,72 |
0,75 |
|
|
. 0,98 |
0,96 |
0,92 |
0,95 |
0,97 |
|
0,97 |
0,91 |
- 0,57 |
0,77 |
0,98 ) |
|
0,89 |
0,82 |
- 0,61 |
0,89 |
0,96 |
|
0,95 |
0,96 |
- 0,62 |
0,71 |
0,92 |
|
0,95 |
0,94 |
- 0,65 |
0,72 |
0,95 |
|
0,86 |
0,80 |
- 0,54 |
0,75 |
0,97 |
|
1 |
0,94 |
- 0,63 |
0,78 |
0,94 |
|
0,94 |
1 |
- 0,67 |
0,77 |
0,88 |
|
- 0, 63 |
- 0,67 |
1 |
- 0,59 |
- 0, 62 |
|
0,78 |
0,77 |
- 0,59 |
1 |
0,82 |
|
0,94 |
0,88 |
- 0,62 |
0,82 |
1 , |
Поскольку коэффициенты корреляции отражают взаимосвязь между двумя признаками под воздействием всех остальных, то следующим этапом исследования является оценка связи между парой признаков, очищенной от влияния всех остальных признаков.
С помощью пакета Statistica получена информация о значении множественного коэффициента корреляции R 1/2_10 = 0,999993 , коэффициента детерминации R 1/2_10 = 0,999986, а также значение F -статистики, предназначенной для проверки гипотезы о незначимости коэффициента детерминации (F = 7704,826) и вероятности принятия данной гипотезы (p = 0,008841). Далее рассчитаны оценки частных коэффициентов корреляции.
Сравнивая по абсолютной величине оценки коэффициентов корреляции и соответствующих частных коэффициентов корреляции, можно сделать следующие выводы.
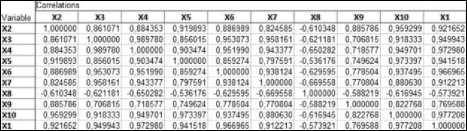
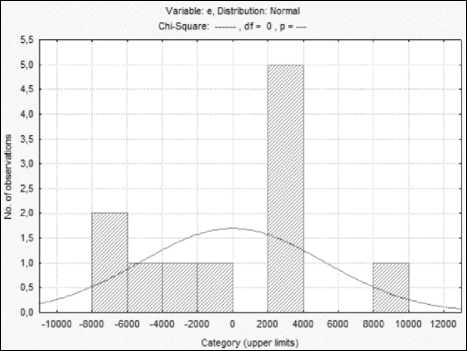
Поскольку r 1,2 = 0,92 < r 1,2/3 – 10 = 0,997, то такие показатели, как среднедушевые денежные доходы населения региона (ξ3), оборот розничной торговли (ξ4), уровень добычи полезных ископаемых (ξ5), объем продукции обрабатывающего производства региона (ξ6), продукция сельского хозяйства (ξ7), удельный вес численности населения в трудоспособном возрасте в общей численности населения региона (ξ8), объем инновационных товаров, работ, услуг (ξ9), а также валовой региональный продукт (ξ10) ослабляют (незначительно) взаимосвязь между парой показателей: инвестиции в основной капитал региона (ξ1) и объем работ, выполненных по виду экономической деятельности «Строительство» (ξ2). Аналогичный результат можно наблюдать для таких пар показателей, как: инвестиции в основной капитал региона (ξ1) и среднедушевые денежные доходы населения региона (ξ3) (т. к. r 1,3 = 0,95 < r 1,3/2,4 – 10 = 0,999), инвестиции в основной капитал региона (ξ1) и оборот розничной торговли (ξ4) (т. к. r 1,4 = 0,97 < Так как r 1,8 = 0,57 < r 1,8/2-7,9 – 10 = 0,999, то такие показатели, как объем работ, выполненных по виду экономической деятельности «Строительство» (ξ2), среднедушевые денежные доходы населения региона (ξ3), оборот розничной торговли (ξ4), уровень добычи полезных ископаемых (ξ5), объем продукции обрабатывающего производства региона (ξ6), продукция сельского хозяйства (ξ7), а также объем инновационных товаров, работ, услуг (ξ9) и валовой региональный продукт (ξ10) ослабляют (значительно) взаимосвязь между парой показателей: инвестиции в основной капитал региона (ξ1) и удельный вес численности населения в трудоспособном возрасте в общей численности населения региона (ξ8). Подобный результат наблюдается и для пары показателей инвестиции в основной капитал региона (ξ1) и объем инновационных товаров, работ, услуг (ξ9) (здесь r 1,9 = 0,77 < <r 1,9/2-8,10 = 0,965), так остальные показатели (ξ2, ξ3, ξ4, ξ5, ξ6, ξ7, ξ8, ξ10) значительно ослабляют связь между рассматриваемой парой показателей. Для пары показателей инвестиции в основной капитал региона (ξ1) и валовой региональный продукт (ξ10) остальные показатели, такие, как объем работ, выполненных по виду экономической деятельности «Строительство» (ξ2), среднедушевые денежные доходы населения региона (ξ3), оборот розничной торговли (ξ4), уровень добычи полезных ископаемых (ξ5), объем продукции обрабатывающего производства региона (ξ6), продукция сельского хозяйства (ξ7), а также удельный вес численности населения в трудоспособном возрасте в общей численности населения региона (ξ8) и объем инновационных товаров, работ, услуг (ξ9) не оказывают никакого влияния, поскольку r 1,10 = 0,98 « r 1,10/2 — 9 = 0,989. Аналогично и для показателей объем инновационных товаров, работ, услуг (ξ9) и валовой региональный продукт ($10), так как r 9,10 = 0,82 ® « r 9,10/1 — 8 = 0,823. Для всех остальных пар признаков следует отметить, что оценки коэффициентов корреляции (по абсолютной величине) больше, чем оценки соответствующих частных коэффициентов корреляции, т. е. наличие других показателей усиливает взаимосвязь между исследуемой парой признаков. С помощью пакета Statistica получена информация об остальных значениях множественного коэффициента корреляции, коэффициента детерминации, а также значении F-статистики, предназначенной для проверки гипотезы о незначимости коэффициента детерминации и вероятности принятия данной гипотезы. Дальнейшим этапом корреляционного анализа – установление значимости характеристик связи (коэффициентов корреляции, частных коэффициентов корреляции и коэффициентов детерминации) на заданном уровне значимости а = 0,05. Это можно реализовать двумя способами. В основе первого способа лежит сопоставление наблюдаемого значения статистики с критическим значением, в случае если |tнабл.| > tкр. (для коэффициентов корреляции и частных коэффициентов корреляции), Fнабл. > Fкр. (для коэффициентов детерминации), то с вероятностью ошибки 0,05 нулевая гипотеза о незначимости соответствующих характеристик связи отклоняется. В основе второго способа лежит сопоставление значения вероятности принятия нулевой гипотезы о незначимости характеристики связи (наблюдаемого уровня значимости p) с заранее установленным уровнем значимости а = 0,05, в случае, если p< 0,05, то на 5%-ом уровне значимости нулевая гипотеза отклоняется и делается заключение о статистической значимости соответствующих характеристик связи. Для проверки значимости коэффициентов корреляции использованы результаты, полученные ранее в пакете Statistica. Критическое значение определим с помощью функции СТЬЮДЕНТ.ОБР.2Х (Вероятность; Степени_свободы) пакета MS Excel [10]. Учитывая заданный уровень значимости а = 0,05 и число степеней свободы v = n - 2 = 11 - 2 = 9 , критическая точка принимает следующее значение t = 2,262157 . Аналогичным образом на основе информации об оценках частных коэффициентов корреляции определена значимость частных коэффициентов корреляции. При а = 0,05 и числе степеней свободы v = n - k = 11 -10 = 1, критическая точка принимает следующее значение tKp = 12,7062 . Используя результаты оценивания множественных коэффициентов корреляции и коэффициентов детерминации, определена значимость коэффициентов детерминации в таблице 3. Для этого рассчитано критическое значение с помощью функции F.ОБР.ПХ (Вероятность; Степени_свободы 1; Степени_свободы 2) табличного редактора MS Excel. Таблица 3. Результаты проверки гипотез о незначимости коэффициентов детерминации Table 3. Results of testing hypotheses about the insignificance of the coefficients of determination Коэффициент детерминации Coefficient of determination Оценка коэффициента детерминации Estimation of the coefficient of determination F набл F кр Вероятность принятия нулевой гипотезы p Probability of acceptance of the null hypothesis p Уровень значимости α Significance level α Значимость Significant ˆ2 R1/2-10 0,999986 7704,83 240,54 0,008841 0,05 + ˆ2 R2 /1,3-10 0,99983 653,81 0,030343 ˆ2 R3/1-2,4-10 0,999992 13409,67 0,006702 ˆ2 R4 /1-3,5-10 0,999995 21037,03 0,005351 2 R5/1-4,6-10 0,999252 148,43 0,063621 – 2 R6/1-5,7-10 0,999952 2300,46 0,016179 + 2 R7/1-6,8-10 0,999705 376,91 0,039955 ˆ2 R8/1-7,9-10 0,999558 251,07 0,048943 ˆ2 R9/1-8,10 0,994242 19,18 0,175493 — ˆ2 R10/1-9 0,999882 944,96 0,025241 + Учитывая заданный уровень значимости α = 0,05 и число степеней свободы v= k- 1 = = 10-1 = 9 , v = n - k = 11 - 10 = 1 , критическая точка принимает значение F = 240, 5433. Дальнейший шаг корреляционного анализа – построение с вероятностью γ = 0, 95 доверительных интервалов для значимых коэффициентов корреляции и частных коэффициентов корреляции с помощью z -преобразования Фишера. Заключительным этапом корреляционного анализа является оценка уравнения регрессии. В качестве результативного признака выбран показатель ξ1 – инвестиции в основной капитал региона. Признаки ξ2 – ξ10 выступают в качестве факторов, оказывающих влияние на объем инвестиций в основной капитал региона. Таким образом, оценка уравнения регрессии имеет вид: xˆ = -262265,89 + 0,51x -11,77x + 1, 03x + +0, 05x + 0, 29x + 0, 36x + 4803, 58x - -0,17x-0/06x Полученное уравнение регрессии относительно признака ξ адекватно выборочным данным (т. е. значимо), так как соответствующий коэффи-2 циент детерминации R является значимым. Значимость коэффициентов уравнения регрессии определяют по итогам исследования значимости частных коэффициентов корреляции. Таким образом, среди коэффициентов уравнения регрессии значимыми оказались β , β , β , β , β поскольку значимы соответствующие частные коэффициенты корреляции ρ1,2/3-10,ρ1,3/2,4-10,ρ1,4/2-3,5-10 , ρ1,6/2-5,7-10 , ρ1,8/2-7,9-10 Следовательно, корреляционно-регрессионный анализ показателей инвестиционной привлекательности Оренбургской области позволяет сделать вывод, что на объем инвестиций в основной капитал региона значимое влияние оказывают следующие факторы: ─ объем работ, выполненных по виду экономической деятельности «Строительство» (млн рублей); ─ среднедушевые денежные доходы населения области (в месяц рублей), оборот розничной торговли региона (млн рублей); ─ объем продукции обрабатывающего производства (в фактически действовавших ценах; млн рублей); ─ удельный вес численности населения в трудоспособном возрасте в общей численности Оренбургской области (проценты). На основании полученного уравнения регрессии следует, что при прочих равных условиях при увеличении объема работ в регионе, выполненных по виду экономической деятельности «Строительство» на 100 млн рублей инвестиции в основной капитал области увеличатся на 51 млн рублей; с увеличением оборота розничной торговли на 100 млн рублей объем инвестиций в основной капитал региона увеличатся на 103 млн рублей; увеличение на 100 млн рублей объема продукции обрабатывающего производства приведет к росту инвестиций в основной капитал области на 29 млн рублей; с увеличением на 1% удельного веса численности населения в трудоспособном возрасте в общей численности населения региона инвестиции в основной капитал возрастут в среднем на 4803,58 млн рублей. Поскольку в процессе проведения корреляционно-регрессионного анализа выявлено подозрение на наличие мультиколлинеарности, то далее проведем более подробное исследование полученной регрессионной модели. Для исследования линейной регрессионной модели на мультиколлинеарность по исходным данным необходимо: 1. построить оценки коэффициентов линейной модели множественной регрессии методом наименьших квадратов (МНК) и провести анализ; 2. провести анализ построенной модели на мультиколлинеарность; 3. устранить мультиколлинеарность при ее наличии. На основе информации об объеме инвестиций в основной капитал Оренбургской области, млн рублей (y), объеме работ, выполненных в регионе по виду экономической деятельности «Строительство», млн рублей (x2), денежных доходов, приходящихся на душу населения области в месяц, руб. (x3), обороте розничной торговли региона, млн рублей (x5), уровне добычи полезных ископаемых, млн рублей (x5), объеме продукции обрабатывающего производства области, млн рублей (x6), объеме продукции сельского хозяйства области, млн рублей (x7), численности трудоспособного населения, в% от общей численности населения субъекта (x8), объеме инновационных товаров, работ и услуг, млн рублей (x9), а также ВРП Оренбургской области, млн рублей (x10) построена линейная регрессионная модель. С помощью пакета Statistica рассчитана оценка множественного коэффициента корреляции Rm_10 = 0,999993. Далее проведено исследование на нормальный характер распределения регрессионных остатков. На рисунке 1 представлена гистограмма распределения регрессионных остатков. Рисунок 1. График распределения регрессионных остатков Figure 1. Graph of the distribution of regression residuals Согласно полученному графику, представленному на рисунке 1, можно предположить, что в разрезе большего временного интервала нулевая гипотеза о том, что распределение регрессионных остатков не отличается от нормального, может быть принята. Так как регрессионные остатки имеют нормальное распределение, то есть смысл проводить дальнейший анализ построенного уравнения множественной регрессии. Отметим, что уравнение регрессии для выбранного признака адекватно выборочным данным – значимо, т. е. модель адекватна экспериментальным данным. Среди коэффициентов уравнения регрессии значимыми оказались коэффициенты при переменных x , x , x , x , x . Среднеквадратические ошибки S при пере менных x, x оказались того же порядка, что и коэффициенты регрессии при этих же переменных. Следовательно, коэффициенты при данных переменных могут иметь доверительный интервал, который содержит точку нуль. Согласно полученной модели, можно сделать следующие выводы: ─ при увеличении на 100 рублей в месяц среднедушевых доходов населения инвестиции в основной капитал региона уменьшатся на 1177 млн рублей (коэффициент при переменной x имеет отрицательный знак); ─ при увеличении объема инновационных товаров, работ, услуг на 100 млн рублей инвестиции в основной капитал региона уменьшатся на 17 млн рублей (коэффициент при переменной x имеет отрицательный знак); ─ при увеличении на 100 млн рублей валового регионального продукта объем инвестиции в основной капитал региона уменьшатся на 6 млн рублей (коэффициент при переменной x имеет отрицательный знак). Полученные выводы противоречат экономическому смыслу. Таким образом, все перечисленные признаки позволяют заподозрить наличие мультиколлинеарности между объясняющими переменными. Рассмотрим критерии по выявлению мультиколлинеарности. Для начала проанализируем оценку матрицы парных коэффициентов корреляции между объясняющими переменными. Считается, что наличие значимых коэффициентов корреляции, по абсолютной величине превосходящих 0,7–0,8, свидетельствует о присутствии мультиколлинеарности. На рисунке 2 представлена оценка матрицы парных коэффициентов корреляции. На основе вычисленной матрицы есть основания подозревать тесную связь между всеми парами переменных, кроме х1 и х8, х2 и х8, х3 и х8, х4 и х8, х5 и х8, х6 и х8, х7 и х8, х9 и х8, х10 и х8. Рисунок 2. Оценка матрицы парных коэффициентов корреляции Figure 2. Estimation of the matrix of paired correlation coefficients Более внимательное изучение этого вопроса достигается с помощью расчета значений коэффициентов детерминации каждой из объясняющих переменных x(j)по всем остальным переменным x(j) = (x(1)…, x(j-1), x(j+1)…, x(p)). Получены следующие результаты оценивания коэффициентов детерминации: R2 x2/x3x4x5x6x7x8x9x10 R2 x3/x2x4x5x6x7x8x9x10 x4/x2x3x5x6x7x8x9x10 x5/x2x3x4x6x7x8x9x10 x6/ x2x3x4x5x7x8x9x10 R2 x7/x2x3x4x5x6x8x9x10 x8/x2x3x4x5x6x7x9x10 R2 x9/ x2x3x4x5x6x7x8x10 R2 x10/x2x3x4x5x6x7x8x9 = 0,968525, = 0,994205, = 0,995287, = 0,980859, = 0,960731, = 0,966417, = 0,655590, = 0,916071, = 0,994329. Анализ оценок коэффициентов детерминации показал наличие тесной линейной связи между всеми объясняющими переменными и остальными признаками. Достаточным условием плохой обусловленности матрицы (наличия мультиколинеарности) является большое значение числа обусловленности: m = (М, (1) | Amin | где λmах – максимальное собственное число матрицы XT X. Для вычисления собственных чисел матрицы XT X использована функция eigenvals из математического пакета Mathcad [12]. Таким образом, получено, что значение числа обусловленности составляет M = 1,915 -108. На основании полученного результата можно сделать вывод, что между всеми объясняющими переменными существует мультиколлинеарность. В случае, если между объясняющими переменными существует частичная мультиколлинеарность, то оценки коэффициентов линейной модели, полученные по МНК, становятся неустойчивыми, незначительное изменение состава выборки или состава объясняющих переменных может вызвать кардинальное изменение модели, что делает модель непригодной для практических целей. Наиболее распространенные в таких случаях приемы оценивания параметров регрессионной модели: методы пошаговой регрессии, использование гребневой регрессии (ридж-регрессии), переход от первоначальных переменных к их главным компонентам. Все вышеприведенные методы реализуются в пакете Statistica. На рисунке 3 представлено исследование регрессионных остатков после оценивания параметров линейной модели множественной регрессии методом пошагового исключения (Backward stepwise). Рисунок 3. Гистограмма распределения регрессионных остатков Figure 3. Histogram of the distribution of regression residuals На основании полученного графика, можно предположить, что в разрезе большего временного интервала нулевая гипотеза о том, что распределение регрессионных остатков не отличается от нормального, может быть принята. Обсуждение В результате проведения пошаговой регрессии получена следующая оценка уравнения регрессии: y = 0,1433x5 + 0,3281x6 + 427,8377x8. (0,0309) (0,0483) (96,2992) Оценка уравнения регрессии значима, т. к. нулевая гипотеза отклонена; коэффициенты при переменных также значимы. Коэффициент детерминации составил 0,9991, т. е. 99,91% доли вариации результирующей переменной объясняется переменными х5, х6 и х8, а 0,09% доли вариации, вероятно, объясняется неучтенными в модели факторами. Другими словами, на изменение объема инвестиций в основной капитал региона большее влияние оказывают такие показатели, как ─ уровень добычи полезных ископаемых; ─ объем продукции обрабатывающего производства; ─ удельный вес численности населения в трудоспособном возрасте. Согласно полученной регрессионной модели, можно сделать выводы о том, что увеличение уровня добычи полезных ископаемых на 100 млн рублей приводит к увеличению объема инвестиций в основной капитал региона на 14,33 млн рублей, а при увеличении на 100 млн рублей объема продукции обрабатывающего производства инвестиции в основной капитал региона увеличиваются на 32,81 млн рублей. Кроме того, объем инвестиций в основной капитал региона увеличиваются на 427,8377 млн рублей при увеличении на 1% удельного веса численности населения в трудоспособном возрасте в общей численности. С экономической точки зрения полученные выводы можно считать адекватными. Заключение На основании результатов корреляционнорегрессионного анализа можно сделать вывод о том, что на уровень объема инвестиций в основной капитал Оренбургской области наиболее значимое влияние оказывают такие сферы экономической деятельности, как сельское хозяйство, добыча полезных ископаемых и обрабатывающие производства. Следовательно, региональным органам управления инвестиционной деятельностью и экономического развития необходимо обратить внимание на реализацию инвестиционного потенциала именно этих отраслей экономики. Привлечение инвестиций в выявленные отраслевые приоритеты инвестиционной привлекательности Оренбургской области обеспечит создание высокопроизводительных мест на территории региона, увеличение валового регионального продукта, а также даст мультипликативный эффект для развития других видов деятельности.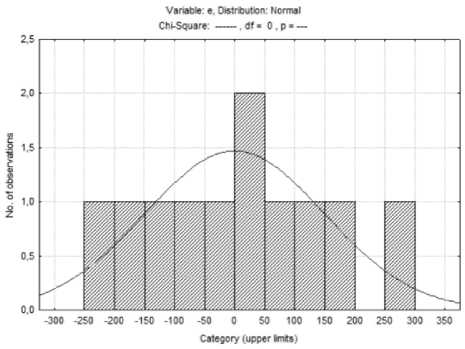
Список литературы Применение методов математической статистики для оценки инвестиционного потенциала региона
- Кособуцкая А.Ю., Равуанжинирина А.В. Инвестиционная привлекательность региона: методики оценки // Вестник ВГУ. Серия: Экономика и управление. 2019. № 1. С. 32-37.
- Литвинцева Г.П., Голдобина А.А. Факторы и пути повышения инвестиционной привлекательности региона // Идеи и идеалы. 2019. №4-2. С. 243-266. doi: 10.17212/2075-0862-2019-11.4.2-243-266
- Болодурина М.П., Мишурова А.И. Стандартизация оценки инвестиционной привлекательности туристско-рекреационного комплекса региона // Национальные интересы: приоритеты и безопасность. 2019. Т. 15. № 11 (380). С. 2108-2127. doi: 10.24891/ni. 15.11.2108
- Чимирис А.С. Анализ инвестиционной привлекательности регионов России // Международный журнал гуманитарных и естественных наук. 2019. № 5-4. С. 143-148. doi: 10.24411/2500-1000-2019-11035
- Валерианов А.А., Дмитриева А.Г., Леванова Т.А. Статистические методы анализа в оценке инвестиционного потенциала региона //Вестник НГИЭИ. 2018. № 6 (85). С. 138-150.
- Дмитриев Н.Д., Родионов Д.Г., Кубарский А.В. Формирование эконометрического инструментария для оценки инвестиционной привлекательности региона// Kant. 2020. №4(37). С. 70-77. doi: 10.24923/2222-243Х.2020-37.15
- Официальная статистика: Территориальный орган Федеральной службы государственной статистики по Оренбургской области. URL: https://orenstat.gks.ru/ofstatistics
- Национальный рейтинг состояния инвестиционного климата в субъектах РФ. Агентство «АСИ»: агентство стратегических инициатив по продвижению новых проектов. Москва: Агентство стратегических инициатив, 2021. URL: https://asi.ru/government_officials/rating/
- Рейтинг инвестиционной привлекательности регионов RAEX за 2020 год: RAEX (РАЭКС-Аналитика): рейтинговое агентство. Москва: РАЭКС-Аналитика. 2020. URL: https://raex-a.ru/ratings/regions/2020#graph
- Соловьёв И.В. Геодезия и прикладная информатика // Вестник МГТУ МИРЭА. 2014. №. 2. С. 3.
- Моисеев Н.А. Сравнительный анализ эффективности методов устранения мультиколлинеарности // Учет и статистика. 2017. № 2 (46). С. 62-73.
- Ерёмина Д.В. Прикладная информатика для специалистов аграрного сектора // Агропродовольственная политика России. 2017. №. 9. С. 98-103.
- Ali E.B., Amfo B. Comparing the values of economic, ecological and population indicators in High - and Low-Income Economies // Ekonomika regiona. 2021. №. 17(1). P. 72-85. doi: 10.17059/ekon. reg.2021-1-6
- Ayres R., Voudouris V. The economic growth enigma: Capital, labour and useful energy? // Energy Policy. 2014. №. 64. P. 16-28.
- Baltina A., Bolodurina M., Gorbatenko E. The application of information technologies in the development of corporate growth strategy // EMIT 2018 Internationalization of Education in Applied Mathematics and Informatics for HighTech Applications. Electronic data. 2018. №. 2093. P. 58-66.
- Ramachandran K.M., Tsokos C.P. Mathematical statistics with applications in R. Academic Press, 2020.
- Gabdrahmanova K.F., Izmailova G.R., Samigullina L.Z. Methods of mathematical statistics application in assessing the density of actual and forecasting distribution density of residual oil reserves // IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2020. V. 860. №. 1. P 012008.
- Zhang Z., Wu Y., Zhang R., Jiang P. et al. Novel transformer fault identification optimization method based on mathematical statistics//Mathematics. 2019. V. 7. №. 3. P. 288. doi: 10.3390/math7030288
- Nodira S., Gulchekhra K., Nodira A., Maprat R. et al. Teaching Currently Using Interactive Methods in Problem" Probability Theory and Mathematical Statistics" // Central Asian journal of mathematical theory and computer sciences. 2021. V. 2. №. 4. P. 26-28.
- Luo W. Application of improved clustering algorithm in investment recommendation in embedded system // Mcroprocessors andMcrosystems. 2020. №. 75. P. 1-8. doi: 10.1016/j.micpro.2020.103066
- Donghyun C. et al. Using genetic algorithm to support clustering-based portfolio optimization by investor information // Appl. Soft Comput. 2017. №. 61. P. 593-602.


