Применение методов оптимизации для определения характеристик термомеханического поведения стеклующихся полимеров

Ключевой проблемой при разработке технологии производства полимерных изделий является определение характеристик материала, связанное с проведением дорогостоящих экспериментов. Поэтому крайне важно искать новые методы обработки и анализа данных измерений, позволяющих получить достоверные результаты в тех случаях, когда эксперимент не дает полной информации.

В качестве альтернативы натурным испытаниям для определения термомеханических характеристик материала предлагается применение методов оптимизации для использования результатов сравнительно небольшого числа экспериментов [1].

1.    Постановка задачи МДТТ

Цилиндр из стеклующегося полимера (эпоксидная смола ЭДТ-10) с заданной геометрией равномерно разогрет, а затем охлаждается до комнатной температуры. По результатам экспериментального определения остаточных напряжений требуется определить параметры (физико-механические константы), адекватно отражающие термомеханическое поведение материала.

Математическая модель, описывающая термомеханическое поведение стеклующегося полимера, представлена в работах [1,2]. Для рассматриваемого полимера существует переходный процесс стеклования, который характеризуется степенью застеклованности N ( T ( t ) ) , ( 0 <  N < 1 ) , показывающей «завершенность» процесса стеклования при температуре T ( t ) .

Математическая постановка квазистатической краевой задачи, описывающей термовязкоупругое поведение изделия, включает уравнения нестационарной задачи теплопроводности (1)–(3), уравнения равновесия (4), соотношения Коши (5), граничные условия (6) и физические соотношения (7).

c р T = XN T ( x , t ) , x e V , t e [ 0, t_K ] , (1)

T ( x ,0 ) = T h ( x ) , x e ( V u 5 1 ) , (2)

Xn• gradT = -h(T(x,t)-Tc), x e 52, t e[0,tK], (3) где c, ρ, λ, h – теплоемкость, плотность, теплопроводность и коэффициент теплоотдачи в окружающую среду; x – радиус-вектор произвольной точки области V u 5; 5 1 u 52 = 5 ; n - вектор единичной внешней нормали к границе S2 ; TH ,Tc – начальная температура и температура среды.

div о ( x , t ) + p f ( x , t ) = 0, x e V , t e [ 0, t K ] ,               (4)

2 s ( x , t ) = V u ( x , t ) + u ( x , t ) V , x e V , t e [ 0, t K ] ,            (5)

о ( x , t ) • n ( x ) = 0, x e S _a , t e [ 0, t_K ] , u ( x , t ) = U ( x , t ) , x e S u , t e [ 0, t_K ] .

σ

( t ) = K 1 ( ^T ( t ) ) - 3 G 1 ( ^T ( t ) ) "® ( t ) g + ² G 1 ( ^T ( t )b( t )

T ( t )

- 3 K 1 ( T ( t ) ) •• / a ( T ) d T ( т ) +

T H

9               1 ^T ( t )

^K 2 ( ^T ( t ) ) — 3 G 2 ( ^T ( t ) ) •• J [® ( t ) -® * ( т ) ] g d ^V ( T ( т ) ) +

^T ( t )

+ ^{2 G} 2 ( ^T ( t ))- J [ s ( t ) — S * ( Т ) ] d ^V ( T ( т ) ) -

T H

^T ( t )

— ^{3 K} 2 ( ^T ( t ) )- J

T H

’ T ( t )                               T ( т )

J a(T(5))dT(5)- J a(T(5))dT(5)

TH                 TH dV (T (т)),

где U , f – векторы перемещений и объемных сил; n – вектор единичной внешней нормали к границе S = S _a и S u области V ; S _а , S _u - части границы S , на которой заданы соответственно поверхностные силы и перемещения; G ₁, G ₂, K ₁, K ₂ – тензоры сдвиговых и объемных модулей материала в высокоэластическом и застеклованном состояниях; α ( T ) – тензор коэффициентов линейного температурного расширения; g - метрический тензор; T - температура; t , т - время.

Физические соотношения могут быть представлены с использованием разложения на девиаторные (8) и шаровые (9) части тензоров напряжений и деформаций:

T ( t )

S(t) = 2G1 (T(t))•• e(t) + 2G2(T(t))•• J (e(t)-e(т))dV(T(т)) (8) TH

о ( t ) = K 1 ( ^T ( t ) ) ••

^T ( t )

0 ( t ) g - 3 J a ( T ) dT ( t )

T H

+

T ( t )

+K2 (t)" J *

T H

^T ( t )

0 ( t ) g - 3 J a ( T ) dT ( 5 )

T H

-

^T ( t )

0 ( t ) - 3 J a ( T ) dT ( 5 )

T H

> dN ( t ) ,

где

e ( t ) = £( t )-0( t ) g, 0( t ) = |Sp£ = 3 £•• g, s (t ) = ° (t )-q( t) g, o( t ) = 3Spo = 3 о •• g.

Здесь α( T ) – коэффициент линейного температурного расширения, T – температура, t , τ – время.

Зависимость степени застеклованности от температуры в соответствии с экспериментальными результатами характеризуется двумя параметрами Tg и у и может быть записана в виде dN     1

—=—j^^exp dT     2πγ

1 f t - Tg Y " 21 Y J

Предполагается, что для девиаторной и шаровой частей тензоров зависимости степени застеклованности от температуры могут быть различными, а следовательно, будут определяться четырьмя параметрами - T g , y ' , t;, y".

d N '     - 1

= exp dt (t) 72Пу'

d N"      - 1

= exp d T (t) Т2Пу"

1 f ^T ( t ) - T g

( y' J

I f T (t)-t; )2

( y'' J

,

.

2.    Постановка задачи оптимизации

В качестве критерия оптимизации выбрана функция, представляющая собой сумму квадратов отклонений напряжений, полученных в результате решения задачи (1)–(7) с заданными параметрами, от со- ответствующих напряжений, найденных экспериментально [1], и записанная в виде

• 5\

3.    Методика и результаты решения задачи

ф(p)=Е(К(p,r)-кr(p,r)|-|кФ-к0|) + Q(pНinf,(12)

=1 \                                                          ri)p где r - точки области, в которых найдены экспериментальные значения разности главных напряжений; кф (p,r)-кr (p,r) - разность главных напряжений, получаемая при заданных значениях параметров оптимизации p и ri; Q(p) - функция штрафа, введенная для выполнения ограничений на параметры оптимизации.

Параметрами оптимизации являются константы, характеризующие зависимость степени застеклованности материала от температуры: T g , у ' , T g , у " (11).

Вводятся обозначения: p 1 = T g , p ₂ = у ' , p ₃ = T g " , p ₄ = у" - компоненты вектора параметров оптимизации р.

Задача оптимизации формулируется следующим образом: найти вектор параметров p = ( p ₁, p ₂, p ₃, p ₄ ) , сообщающих минимум функции (12) при ограничениях в виде задачи (1)-(7).

Ввиду осевой симметрии задачи для уменьшения размерности конечно-элементной сетки рассматривается только четверть сечения цилиндра (рис. 1).

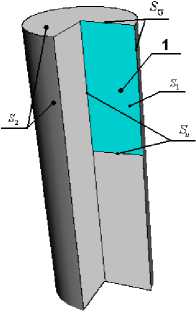
Рис. 1. Расчетная схема цилиндра

Решение задачи теплопроводности (1)(3) выполнено с использованием явной схемы метода конечных разностей [3] в пакете MATLAB . На рис. 2 представлена зависимость изменения максимальной температуры в центральном сечении цилиндра от времени.

Для решения задачи термовязкоупругости разработана оригинальная компьютерная программа, реализующая метод конечных элементов [4] с учетом особенностей математической постановки.

Минимизация функции четырех переменных (12) выполнялась методом Нелдера-Мида [5]. Для исследования единственности решения поиск минимума проводился при различных начальных приближениях. Координаты некоторых начальных точек приведены в табл. 1. Эволюция значений критерия оптимизации при выполнении процедуры поиска минимума целевой функции (12) методом Нелдера-Мида для приведенных в табл. 1 начальных приближений показана на рис. 3 и 4.

Решение задачи оптимизации при всех выбранных начальных приближениях сходится к значениям параметров, представленным в табл. 2.

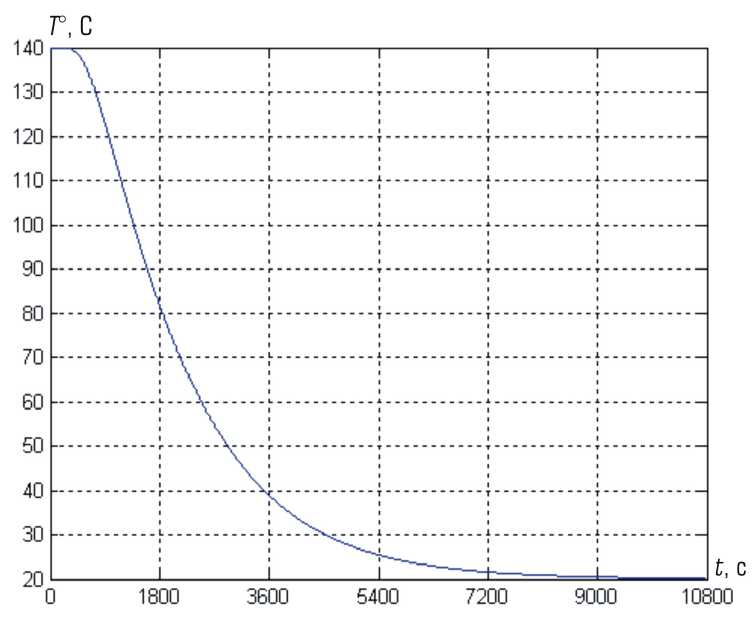
Рис. 2. Изменение максимальной температуры в сечении цилиндра в зависимости от времени

Таблица 1

Начальное приближение 1						Начальное приближение 2
Номер вершины симплекса	p 1	p 2	p 3	p 4		Номер вершины симплекса	p 1	p 2	p 3	p 4
1	100	4,2	78	4,5		1	110	4,6	40	1,9
2	75	4,0	80	5,0		2	50	3,0	95	6,3
3	96	3,7	88	3,5		3	70	1,7	80	4,5
4	50	5,0	70	6,0		4	30	8,0	50	4
5	82	3,2	90	4,7		5	90	4,2	100	3,7

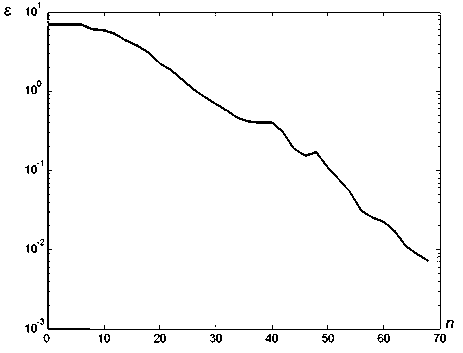
Рис. 3. Зависимость решения задачи оптимизации от количества шагов метода Нелдера-Мида при начальном приближении 1

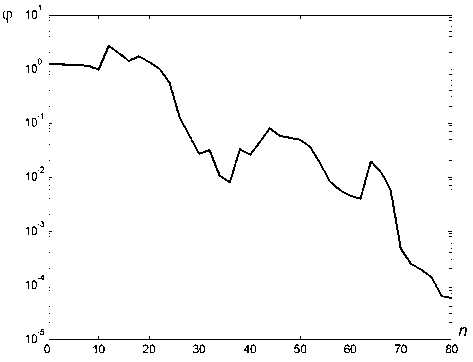
Рис. 4. Зависимость решения задачи оптимизации от количества шагов метода Нелдера-Мида при начальном приближении 2

Таблица 2

Оптимальные значения параметров степени застеклованности

p 1	p 2	p 3	p 4
53,5	5,4	72,6	6,5

Предложена методика, позволяющая определять физико-механические константы полимера с применением методов оптимизации при сравнительно небольшом объеме экспериментальных данных.

Для реализации предложенной методики разработаны оригинальные компьютерные программы, учитывающие допущение о том, что термомеханическое поведение материала описывается для шаровой и девиа-торной частей тензоров напряжений и деформаций разными константами.

Анализ полученного решения задачи оптимизации, приведенного в табл. 2, показывает, что для девиаторных и шаровых частей тензоров напряжений и деформаций значения параметров T_g ′ и T_g ′′ различаются на 36 %. Это подтверждает предположение о том, что при решении задач определения напряженно-деформированного состояния изделий из исследуемого материала необходимо использовать разные параметры степени стеклования для шаровой и девиаторной частей тензоров напряжений и дефомаций.