Применение минимально избыточной модулярной арифметики для выполнения криптографических преобразований в системе RSA
Автор: Коляда Андрей Алексеевич, Кучинский Петр Васильевич, Червяков Николай Иванович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 3 т.14, 2016 года.
Бесплатный доступ
Статья посвящена проблемам создания и параметризации математического обеспечения криптографических RSA-преобразований с применение минимально избыточной модулярной арифметики (МИМА). Представляемая разработка включает МИМА-алгоритмизацию метода умножения с квадрированием для возведения в степень по модулю криптосистемы, а также синтез алгоритма расчета коэффициента денормировки вычислительной схемы данной операции. Описанный алгоритм возведения в степень базируется на оптимизированной мультипликативной МИМА-процедуре типа Монтгомери. Реализация с его помощью криптографического преобразования по модулям разрядностью 1024 … 2048 бит на ПЭВМ с процессором intel core i5 (тактовая частота 2,27 ГГц) в среднем занимает время порядка 0,56 … 5,67 с. Для расчета денормирующего коэффициента создан новый мультипликативно-субстрактивный метод и на его основе синтезирован простой и эффективный алгоритм, время работы которого на персональной ЭВМ не превышает 13,3 мин.
Криптосистема rsa, криптографическое rsa-преобразование, модулярная система счисления, интервально-индексные характеристики, минимально избыточная модулярная арифметика, умножение монтгомери
Короткий адрес: https://sciup.org/140191908
IDR: 140191908 | DOI: 10.18469/ikt.2016.14.3.01
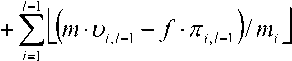
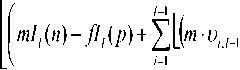
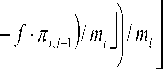
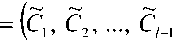
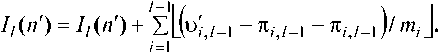
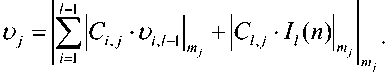
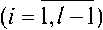
Список литературы Применение минимально избыточной модулярной арифметики для выполнения криптографических преобразований в системе RSA
- Bajard J.-C., Imbert L. A Full RNS Implementation of RSA//IEEE Trans. Comp. V. 53, N 6, 2004. -P. 769-774 DOI: 10.1109/TC.2004.2
- Lim Z., Phillips B.J. An RNS-Enhanced microprocessor implementation of public key cryptography//Signals, Systems and Computers. ACSSC 2007. Conf. Rec. of the forte-first Asilomar Conf. 2007. -P. 1430-1434 DOI: 10.1109/ACSSC.2007.4487465
- «Параллельная компьютерная алгебра. Всероссийская НК с элементами научной школы для молодежи». Ставрополь, октябрь, 2010. Сборник научных трудов. Ставрополь: ИИЦ «Фабула», 2010. -364 с.
- Червяков Н.И. Применение искусственных нейронных сетей и системы остаточных классов в криптографии. Москва: Физматлит, 2012. -280 с.
- Лавриненко А.Н., Червяков Н.И. Округление чисел по модулю поля эллиптической кривой при выполнении криптографических преобразований в системе остаточных классов//Инфокоммуникационные технологии. Т.12, №2, 2014. -С. 4-7.
- Wu Tao, Lee Shoguo, Leu Litian. Improved RNS Montgomery modular multiplication with residue recovery//Proc. Int. Conf. on soft computing techniques and engeneering aplication advances in intelligent systems and computing. V. 250, 2014. -Р. 233-245.
- Schinianakis D., Stouraitis T. Multifunction recidue architectures for cryptography//IEEE Trans. Circuits and Syst. I., 2014. -P. 1156-1169 DOI: 10.1109/TCSI.2013.2283674
- Bigou K., Tisserand A. RNS modular multiplication through reduced base extensions//25 Int. Conf. «Application specific systems, architectures and processors (ASSAP 2014)». Zurich, Switzerland, June, 2014. -P. 57-62.
- Червяков Н.И., Дерябин М.А., Лавриненко И.Н. Реализация алгоритма Монтгомери в системе остаточных классов на базе эффективного алгоритма расширения системы оснований//Нейрокомпьютеры: разработка, применение. № 9, 2014. -С. 37-45.
- Первая МК «Параллельная компьютерная алгебра и ее приложения в новых инфокоммуникационных системах». Ставрополь, октябрь, 2014. Сборник научных трудов. Ставрополь: ИИЦ «Фабула», 2014. -568 с.
- Коляда А.А., Чернявский А.Ф. Умножение по большим модулям с использованием минимально избыточной модулярной схемы Монтгомери//Информатика. № 3, 2010. -С. 31-48.
- Чернявский А.Ф., Коляда А.А., Коляда Н.А. и др. Умножение по большим модулям методом Монтгомери с применением минимально избыточной модулярной арифметики//Нейрокомпьютеры: разработка, применение. № 9, 2010. -С. 3-8.
- Каленик А.Н., Коляда А.А., Коляда Н.А., Чернявский А.Ф., Шабинская Е.В. Умножение и возведение в степень по большим модулям с использованием минимально избыточной модулярной арифметики//Информационные технологии. № 4, 2012. -С. 37-44.
- Коляда А.А., Коляда Н.А., Мазуренко П.А., Чернявский А.Ф., Шабинская Е.В. Таблично-сумматорная алгоритмизация минимально избыточной модулярной схемы Монтгомери для умножения по большим модулям//Наука и военная безопасность. № 3, 2013. -С. 40-45.
- Коляда А.А., Пак И.Т. Модулярные структуры конвейерной обработки цифровой информации. Минск: Университетское, 1992. -256 с.
- Коляда А.А., Чернявский А.Ф. Интегрально-характеристическая база модулярных систем счисления//Информатика. № 1, 2013. -С. 106-119.
- Коляда А.А., Чернявский А.Ф. Интервально-индексный метод четного модуля для расчета интегральных характеристик кода неизбыточной МСС с симметричным диапазоном//Доклады НАН Беларуси, 2013. Т. 57, № 1. -С. 38-45.
- Kawamura S., Koike Masanobu, Sano Fumihiko, Shimbo Atsushi. Cox-Rower architecture for fast parallel Montgomery multiplication.//Eurocrypt, 2000, LNCS. Vol. 1807. Berlin, 2000. -P. 523-538.
