Применение многомерного нормального распределения для построения вероятностной оценки компетентности

Оценка компетентности студентов в вузе является одной из важнейших задач эффективности подготовки конкурентоспособных специалистов, в том числе экологов. Образовательные стандарты третьего поколения предписывают внедрение компетентностно – ориентированного обучения в вузе.

Компетенция – это предметная область, в которой индивид хорошо осведомлен и в которой он проявляет готовность к выполнению профессиональной деятельности. Компетенция – это ситуативная категория, так как она выражается в готовности к осуществлению деятельности в конкретных профессиональных ситуациях. Компетентность – интегральная характеристика личности, распадающаяся на спектр отдельных компетенций , включает в себя когнитивные, мотивационно-ценностный и эмоционально-волевой компоненты.

Основные признаки или факторы компетенции можно оценить, используя таксономию Блума, согласно которой каждая компетенция может быть оценена по шести признакам: знание, понимание, применение, анализ, синтез и оценка.

Согласно ФГОС ВО (уровень бакалавриата) у выпускника должны бать сформированы общекультурные (ОК), общепрофессиональные (ОПК), профессиональные (ПК) и профессионально-прикладные (ППК) компетенции. Для каждого из направлений обучения имеются свои задачи формирования необходимых компетенций будущего специалиста, в том числе в области экологии [1-10].

Рассматривая соответствующий набор компе-тенцийкак n -мерныйвектор X = ( X 1 , X 2 ,...,X_n ) ,

получим четыре вектора компетентностей X' ,. Х„„„. Х„,. Х„ „„с Согласно таксономии ОК ОПК ПК ППК

Блума каждая компонента вектора компетентности будет иметь шесть оценочных значений. Каждому признаку может быть присвоен весовой коэффициент и рассчитан обобщенный показатель оценки компетенции как компоненты соответствующего вектора компетентности.

Чтобы получить среднее значение оценки компетенции каждого вектора необходимо иметь набор многомерных статистических данных, полученных в результате опроса и тестирования специалистов данной предметной области.

Эти данные подлежат систематизации и обработке с целью выявления характера и структуры взаимосвязей между компонентами n -мерного вектора Х = ( X 1 ,X 2 ,...,X n ) . Эти задачи можно решить методами многомерного статистического анализа.

Многомерные статистические методы позволяют обоснованно выбрать ту модель, которая наилучшим образом соответствует исходным статистическим данным, характеризующим реальное поведение исследуемой совокупности объектов, оценить надежность и точность выводов, сделанных на основании ограниченного статистического материала.

Рассмотрим более подробно многомерное нормальное распределение, так как многомерные методы, основанные на нормальном распределении, нашли широкое распространение и их можно изучать более организованно и систематически. Одномерное нормальное распределение возникает очень часто, потому что изучаемый эффект является суммой действия многих независимых случайных факторов. Подобно этому многомерное нормальное распределение часто встречается в связи с тем, что множественные измерения являются суммами многих малых независимых воздействий. Кроме того, для теории нормального распределения разработаны точные математические методы.

Одномерная нормальная плотность распределения может быть записана следующим образом:

- 1 a ( x - ^{р ) 2}            - 1 ⁽ x - ^{р )а (} x - р)

к • e ²        = к • e ²

f a_n  ,„ ' = f ,-   . i . ² p '

V ^ 21   . 22 )  V . 2 .P   . 2   )

где а - положительно, а к выбирается таким образом, чтобы интеграл от (1) по всей оси х был равен единице. Плотность вероятности многомерного нормального распределения величин X 1 ,..., X n имеет аналогичную форму. Скалярная переменная х заменяется вектором

где . 12 является дисперсией X 1 , . 2 ² - дисперсией X 2 и p - коэффициентом корреляции между X 1 и X 2 .

Плотность вероятности X 1 и X 2 равна

^f x ¹ '

x = :

V x n )

скалярную постоянную Р заменяют вектором

' Д ! '

д = ^:

V ^д )

а положительную постоянную а заменяют положительно определенной (симметрической) матрицей

' a11    a12           aln a„  a^ . a,

^{21        22}                 2 n

I a .    a ,           a J n1      n2               nn

Выражение a ( x - р ) ² = ( x - рр ( x - рР в этом случае заменяется квадратичной формой

( x - д ) T A ( x - д ) = j a_tj ( x, - д , ) ( x j - Д j ) . (5)

i, j = 1

Тогда плотность вероятности n -мерного нормального распределения равна

f ⁽ x i

x n ) =

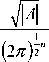
^- 1 ^{( x} - д ⁾ T A ^{( x} - д ⁾ e ²

( 2 ^ ) 2 ⁿ И

- 1 1 ^{x -} д ⁾ T ^{2 1 x -} д ⁾ 2 e ²

где 2 есть ковариационная матрица, равная A ¹ .

Для двумерного нормального распределения полученная модель описывается следующим об-

разом.

Среднее значение вектора X = ( X 1 , X 2 ) T равно

M

^f X

V X 2 )

f д '

V ^д 2 )

ковариационная матрица может быть записана

следующим образом:

^{( X} 1 ^- Д ^{) 2       ( X} 1 ^{- д} 1 ^{)( X} 2 ^{- д} 2 ) '

V ( X 2 - д 2 )( X 1 - д )     ( X 2 - д 2 ) ²    )

2 ^. 1 . _2Л/ 1 - p р

exp <

2 ( 1 - p ² )

_{2 p} ^{( x} 1 ^- д 1 ^{)( x} 2 ^- д 2 ⁾ ₊

. 1 . 2

^{( x} 1 - д 1 ^{) 2}

⁽ x 2 ^- д 2 ^{) 2} . 2

Отметим, что плотность вероятности (6) в n -мерном евклидовом пространстве постоянна на эллипсоидах

( x - д ) ^т 2 ^{- 1} ( x - д ) = c (10) для каждого положительного значения с . Центром каждого эллипсоида является точка д . Форма и положение эллипсоида определяются значением 2 , а размеры - значением с .

Рассмотрим подробно двумерный случай плотности вероятности (9). Преобразуем координаты, переходя к стандартным нормальным случайным величинам по формуле

x , - д ,

—----- = y i ( i =1, 2), так, чтобы центры линий,

.

на которых плотность распределения постоянна, находились в начале координат. Эти линии определяются уравнениями

⁽ У 1 ^{2 -} 2 Р У 1 У 2 ⁺ У 2 ^{2 )}= c .       ⁽¹¹⁾

1 - p

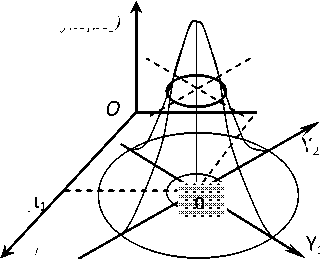
Отрезки, отсекаемые на осях y 1 и y 2 равны между собой. Если p >  0 , то большая ось эллипса наклонена под углом 45⁰ к оси х и ее длина равна 2 -^с ( 1 + p ) , а длина малой оси равна 2 д/ с ( 1 - p ) . Если p <  0 , то большая ось эллипса наклонена под углом 135⁰ к оси х и ее длина равна 2 д/ с ( 1 - p ) , а длина малой оси равна 2 д/ с ( 1 + p ) (рис. 1).

Одной из причин изучения многомерных нормальных распределений является то, что частные и условные распределения, полученные из многомерных нормальных распределений, также нормальны. Линейные комбинации нормально распределенных величин также распределены нормально.

Нормальное распределение полностью определяется вектором д среднего значения и кова-

риационной матрицей 2 . Первой статистической проблемой является вопрос о том, как оценить эти параметры по результатам выборки.

Как и в одномерном случае, методом максимального правдоподобия можно показать, что оценкой для Ц является выборочное среднее, оценкой для 2 - матрица, пропорциональная матрице дисперсий и ковариаций. Выборочная дисперсия равна сумме квадратов отклонений наблюденных значений от выборочного среднего, деленной на число наблюдений без единицы; выборочная ковариация определяется подобным образом по результатам взаимных произведений соответствующих отклонений. Выборочная ковариационная матрица является несмещенной оценкой 2 .

Метод наибольшего правдоподобия очень полезен для различных оценок и проблем проверки гипотез, относящихся к многомерным нормальным распределениям. Оценки, полученные по методу наибольшего правдоподобия, или их модификация обычно обладают некоторыми оптимальными свойствами – асимптотически эффективны.

Если x_v...,X N образуют выборку из многомерного нормального распределения с параметрами Ц и 2 , где ⁿ j = ^{П П} р ( p j = 1 ), то оценкой наибольшего правдоподобия для Ц являет-

N ся ц = x = -772 xa , оценкой наибольшего

N a = 1

правдоподобия для     П²     является

П ²

i

=^{2 (} x a

N а

x ⁾ , где x есть i- я компонента а

Х _а и x есть i- я компонента x , а оценка наибольшего правдоподобия для p j равна

У x x - Nxx - а j a            г j

______а__________________________ z x ² - Nx ²     x ² - Nx ²

ia                        ja           j a                a

a

П

j

П П . (12) j

В одномерном случае выборочное среднее распределено нормально и не зависит от выбо- f(X1,X2)

μ

Y

μ 2    ^{X 2}

X 1

Рис. 1. Поверхность плотности нормального двумерного распределения рочной дисперсии. Аналогично выборочное среднее x = (x1 ... xn)T распределено нормально и не зависит от 2.

Среднее значение выборки объема N из многомерной нормальной генеральной совокупности N ( ц, 2 ) распределено нормально

I 1          1

N I ц —2 I и не зависит от 2 , являющейся

Г N J оценкой наибольшего правдоподобия для 2 .

Одна из наиболее важных групп задач одномерной статистики связана с вопросами, касающимися оценки математического ожидания неко- торого распределения, дисперсия которого неизвестна. Бывают случаи, когда по выборке хотят решить, равно ли математическое ожидание не- которому наперед заданному числу, или же ука- зать интервал, в котором находится математическое ожидание. В одномерных случаях обычно используется статистика, являющаяся частным от деления разности между выборочным значением x и гипотетическим математическим ожиданием генеральной совокупности на среднее квадратическое отклонение s. Если выборка произведена из совокупности N(ц, п2), то величина t = -x-Ц = NN(x - ц)5-1 (13) sN имеет t-распределение с N-1 степенями свободы, где N – объем выборки. Основываясь на этом можно построить критерий для проверки гипотезы Hо: Ц = Цо, где Цо - заданное число, или построить доверительный интервал для неизвестного параметра Ц .

Многомерным аналогом квадрата величины t , определенной формулой (13), является величина т ² Хотеллинга:

T ² = N ( x - ц ) T S ^{- 1} ( x - ц ) , (14) где x – вектор среднего значения и S – ковариационная матрица выборки объема N . Покажем, как можно использовать эту статистику для проверки гипотезы о векторе среднего значения генеральной совокупности Ц и для получения доверительных областей для неизвестного параметра Ц .

Если Ц есть среднее значение многомерного нормального распределения N ( ц , 2 ) , то вероятность получить выборку объема N со средним x = ( x .. x n ) T и выборочной ковариационной матрицей S такую, что

T ² = N ( x - ц ) T S ^{- 1} ( x - ц ) < T ₀²( a ) (15) равна 1 - a .

Здесь

2 _ ⁽ N 1 ) n       / \

T 0 N _- n F n , ^N - n ^{( tt )} ,      ⁽¹⁶⁾

где tt — уровень значимости, Fn N_n (tt) точка F- распределения.

Таким образом, если для конкретной выборки произвести вычисления по формуле (15), то утверждение относительно Д , выраженное формулой (15), будет справедливо с доверием 1 - а . Совокупность точек, координаты которых удов- летворяют неравенству

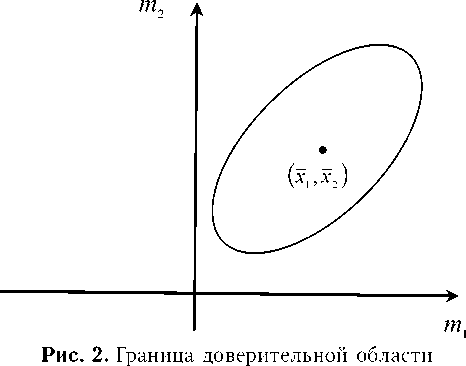
N ( x - m ) ^TS ^{- 1} ( x - m ) < T ₀²( tt ) (17) образует в n -мерном пространстве внутренность и границу эллипсоида с центром в точке X = ( X 1 .. . X n ) T , размеры и форма которого зависят от S ^{- 1} и tt (рис. 2), Д лежит внутри этого эллипсоида. Эллипсоид (17) является случайным, так как выборка случайна.

Описанная модель многомерного нормального распределения использовалась при оценке уровня профессиональной компетентности студентов квалификации – бакалавр по направлению подготовки 080100.62 Экономика. В качестве компонентов вектора Х ПК оценивались две компетенции: способность на основе описания экономических процессов и явлений строить стандартные теоретические и эконометрические модели, анализировать и содержательно интерпретировать полученные результаты (ПК 4); способность использовать для решения аналитических и исследовательских задач современные технические средства и информационные технологии (ПК 8). Таким образом, вектор Х ПК рассматривается как двумерный вектор компетентности, формирование и оценка уровня которого проводилась при изучении дисциплины “Эконометрика” на третьем курсе обучения. Каждая компетенция оценивалась по таксономии Блума.

В качестве диагностических средств были использованы: тесты достижения для оценки уровней знания и понимания; представление и защи-

та итоговой работы по дисциплине, которая включала в себя обработку, анализ и расчет эконометрических показателей с помощью средств ЭВМ (пакет “Анализ данных” Excel), построение эконометрических моделей и их использование для построения прогнозов. При использовании данного средства диагностики оценивались уровни применения, анализа, синтеза и оценки.

Результаты диагностики компетенций в группе из 25 студентов представлены в табл. 1.

Для получения обобщенных показателей уровня компетенций использовались весовые коэффициенты: а 1 =0,05, tt ₂ =0,05, « 3 =0,1, tt 4 =0,2, tt ₅ =0,2, tt ₆ =0,4.

Результаты расчетов обобщенных показателей каждой компетентности приведены в табл. 2.

Найдем оценки математических ожиданий, дисперсии и коэффициента корреляции, доверительную область для вектора математических ожиданий с надежностью Y =0,95.

Точечные оценки для Д 1 и Д 2 - средние арифметические x 1 и x 2 равны:

X 1 = 25(27,3 + 30,1 + ... + 70,3) = 46,72, X ₂ = -25(29,05 + 30,2 + ... + 51,25) = 29,584 .

Для определения ковариационной матрицы S выборки перейдем к цен т рированным случайным величинам u j = X j - X j :

_T (- 19,42 - 16,62 ... 23,58 A

= (- 10,534 - 9,384 ... 11,666^.

( - ^19,42

U ^T U =

< - 19,42

(- 10,534

- 16,62 . 23,58 ^ - 16,62

- 9,384 . 11,666^    -

I 23,58

- 10,534 <

- 9,384

^

11,666 J

< 13652,78 8762,803 <

( 8762,803 6320,309 J

Несмещенная оценка матрицы 2 - ковариа- ционная матрица S выборки равна

13652,78 8762,803

S =---- U T U = —      ,        ,

N - 1        24 ( 8762,803 6320,309

_ < 568,87 356,12 )

= ( 365,12 263,35 J

Таким образом, несмещенные оценки дисперсий и средних квадратичных отклонений следующие: s , ² = 568,87; s 1 = 23,85; s ₂ ² = 263,35; s ₂ = 16,23.

Вычислим выборочный коэффициент корреляции

356,12

.0 =-------------

'’ 23,85 - 16,23

= 0,92.

Обратная матрица к S будет иметь вид

Таблица 1. Результаты формирования профессиональных компетенций в %

Номер студента в списке группы	Ком пе-тенция	Знание	Понимание	Применение	Анализ	Синтез	Оценка
1	ПК 4	61	61	58	23	20	17
	ПК 8	63	60	59	25	20	20
2	ПК 4	64	60	59	25	23	21
	ПК 8	64	64	60	26	23	20
3	ПК 4	53	50	43	18	19	16
	ПК 8	57	52	45	17	19	17
4	ПК 4	54	51	50	22	21	20
	ПК 8	57	52	52	23	20	19
5	ПК 4	72	69	69	44	40	43
	ПК 8	70	70	69	43	40	40
6	ПК 4	69	54	53	30	29	19
	ПК 8	68	55	50	28	29	20
7	ПК 4	74	65	44	23	21	18
	ПК 8	72	65	42	20	20	20
8	ПК 4	57	49	43	18	17	17
	ПК 8	56	50	46	18	18	16
9	ПК 4	74	75	67	34	23	21
	ПК 8	75	74	63	31	24	20
10	ПК 4	44	30	27	12	14	12
	ПК 8	49	32	27	11	11	13
11	ПК 4	69	70	68	34	32	18
	ПК 8	64	63	62	31	29	17
12	ПК 4	38	30	28	12	11	12
	ПК 8	40	30	30	11	10	12
13	ПК 4	49	44	35	18	19	19
	ПК 8	45	44	37	18	17	16
14	ПК 4	69	65	63	43	35	27
	ПК 8	71	67	64	42	35	29
15	ПК 4	68	68	64	23	19	20
	ПК 8	67	66	65	22	19	21
16	ПК 4	100	98	88	69	58	63
	ПК 8	72	70	68	59	53	55
17	ПК 4	100	100	97	69	62	65
	ПК 8	65	66	63	44	45	43
18	ПК 4	100	100	95	87	79	72
	ПК 8	73	70	68	56	53	58
19	ПК 4	100	100	97	78	82	68
	ПК 8	89	89	83	62	67	60
20	ПК 4	100	93	85	62	65	54
	ПК 8	85	78	70	44	50	43
21	ПК 4	100	95	95	78	72	76
	ПК 8	92	90	90	67	72	65
22	ПК 4	100	100	98	87	82	72
	ПК 8	64	62	59	32	34	50
23	ПК 4	100	80	78	55	52	65
	ПК 8	73	65	55	44	46	51
24	ПК 4	100	100	98	60	62	78
	ПК 8	95	95	91	53	51	56
25	ПК 4	100	100	99	66	64	61
	ПК 8	96	91	85	44	45	39

Таблица 2. Обобщенные показатели профессиональных компетенций в %

Номер студента в списке группы	ПК 4 ( х 1 )	ПК 8 ( х 2 )
1	27,3	29,05
2	30,1	30,2
3	23,25	23,95
4	26,85	26,85
5	47,95	46,5
6	30,85	30,55
7	27,35	27,05
8	23,4	23,5
9	33,95	32,75
10	16,4	16,35
11	34,15	31,35
12	15,6	15,5
13	23,15	21,55
14	39,4	40,3
15	29,6	29,75
16	69,3	58,3
17	71,9	47,85
18	81,5	58,95
19	78,9	67
20	65,15	51,15
21	79,65	71,9
22	82,4	45,4
23	64,2	50,8
24	75,4	61,8
25	70,3	51,25

, Г 0,01596    - 0,02213)

5 ^{- 1} =      ,                  ,

(- 0,02213 0,03448 ) ^.

По формуле (14) находим значение статис тики Хотеллинга

,      .                      .( 0,01596 - 0,02213Y 46,72 - а 4

T2 = 25-(46,72 - а 29,584 - ц )                                      I = v 1              \- 0,02213 0,03448 )(29,584 - ц2)

= 0,399 ( 46,72 - ц ) 2 - 1,1065 ( 46,72 - ц )( 29,584 - ц ) + 0,862 ( 29,584 - ц ) 2 .

При уровне значимости а = 1 - у = 0,05 и числе степеней свободы v , = 2 и v ₂ = 23 находим по таблице точку F -распределения - F ( 0,05 ;2;23 ) = 3,42 .

Тогда по формуле (16)

T ² = ----- 3,42 = 7,137

⁰ 25 - 2 ,        , ^.

Из неравенства (17) получим уравнение эллипса (включая внутреннюю область)

0,399 ( 46,72 - a J² - 1,1065 ( 46,72 - ц ₁ )( 29,584 - ц ₂ ) +

+ 0,862 ( 29,584 - ц ₂ ) ² <  7,137 ’ которое определяет доверительную область для вектора средних значений.

Пусть вектор Х подчиняется n -мерному нормальному распределению N_n ( ц , X ) , а матрица С_{п х к} — матрица ранга k ( k <  n ). Тогда вектор

C T X подчиняется k -мерному нормальному распределению N_k ( С ^т а , С ' X С ) , так как линейные комбинации нормально-распределенных величин также распределены нормально.

В этом случае статистика T 2 Хотеллинга имеет вид

T ² = N ( с^тХ - C ^ta ) ^t ( c ^t sc ) ^{- 1} ( c^Tx - C ^ta ) (18)

со значением, отвечающим вероятности а = 1 - у

• 2 ₌ ( N -l) ^k       / ч

• ^т 0 _{м 1}^Fk , N - к ^{( а )} .           ⁽¹⁹⁾

N - к

Поскольку вектор С^тц содержит к генеральных средних, то в отличие от уравнения (16) теперь число степеней свободы равно k и N-k . В частном случае, когда С – единичная матрица порядка n , то уравнение (18) сводится к уравнению (16) и число степеней свободы становится прежним.

Использование линейных комбинаций компонент вектора Ц позволяет расширить область применения статистики T 2 Хотеллинга при интервальном оценивании в задачах сравнения.

С помощью линейных комбинаций можно найти совместные доверительные интервалы или проверить гипотезу относительно первых ( к <  П ) средних значений генеральной совокупности. Для этого достаточно принять

C

(1 )

¹ 0 ^{- 00 - 0}

О  1       000

:                               :::

00 - 10 -

'----------------V----------------' '-----------V'

у к               n - к у

Поскольку С^т имеет размерность к х n и ранг к , то вектор С Ц имеет размерность к х 1 и содержит k генеральных средних.

Чтобы построить доверительный интервал для генерального среднего Ц (j = 1,2,..., n), достаточно принять, что Cj есть j-й столбец единичной матрицы размерности n. Тогда Cj Ц = Ц и статистика Хотеллинга

2 = NCj (Х - ц)]1

CTSC

имеют распределение, зависящее от числа степеней свободы 1 и N -1.

Таким образом, согласно уравнению (18) доверительная область для С Ц с надежностью У будет ограничена поверхностью

N ( С ^т х - С ц) ( С^С ) ^- 1 ( С ^т х - С ^т ц ) = ^{k (} N - ¹⁾ F k _N - к ( а ).(22) N - к

В частности, с надежностью У доверитель ные границы для линейной комбинации С Ц определяются как

СХ ± /С<Сёл^ > .   (23)

По данным табл. 1 с помощью линейных комбинаций найдем с надежностью у = 0,95 интервальные оценки генеральных средних Ц 1 и Ц 2 .

В нашем случае rz 1-у 095 v1 =1 v2 =N-1=24.

Согласно таблице F -распределения точка F (0,05 1; 24)=4,26.

Для построения интервальной оценки средней ц примем С 1 = (1,0) ^Т , так что С ^ х = 46,72; С^т_х8С_х = S 12 = 568,87 . Тогда границы доверительного интервала для Ц 1 имеют вид

46,72 + _л    • 568,87 • 4,26 = 46,72 + 9,85

25                                    .

Откуда

36,87 <  Ц <  56,57 .

Для построения интервальной оценки генерального среднего Ц 2 принимаем С 2 = (0,1) T , откуда С т х = 29,584; С^т , 8С ₂ = S ₂ ² = 263,35 .

Тогда границы доверительного интервала для Ц 2 имеют вид

29,584 + _Л — • 263,35 • 4,26 = 29,584 + 2,06 25                                    ^.

Доверительная

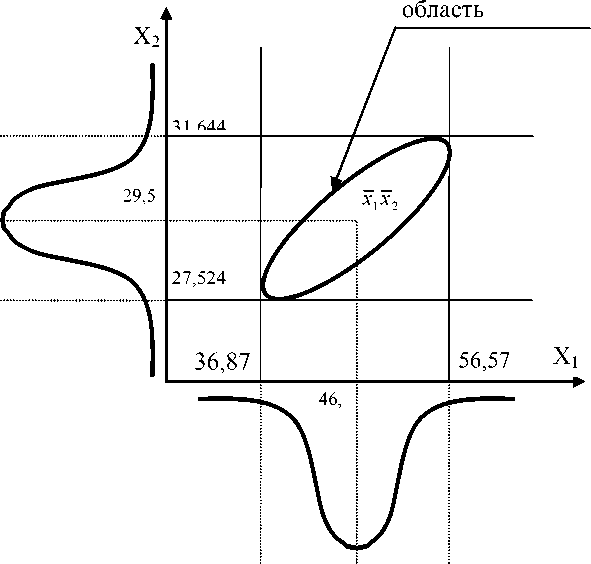
Рис. 3. Доверительная область для двумерного вектора Ц средних

Откуда

27,524 <  Д ₂ <  31,644 .

Доверительная область для двумерного вектора Д средних представлена на рис. 3.