Применение моделей искусственного интеллекта в приемо-сдаточных испытаниях
Автор: Тарасов А.А., Лезина И.В.
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Новые информационные технологии
Статья в выпуске: 2 (82) т.21, 2023 года.
Бесплатный доступ
Данная статья рассматривает применение нейросетевых методов, а именно нечеткого персептрона, в задачах, требующих проведение приемо-сдаточных испытаний. Было проведено исследование по использованию различных нечетких функций при решении задачи аппроксимации плотностей вероятностей. Эксперименты проведены на временных рядах с известными законами распределения, с оценкой качества аппроксимации через среднеквадратичное отклонение в серии из 29 испытаний. В результате исследований при использовании Гауссовой функции принадлежности было получено среднее значение среднеквадратического отклонения равное 00145, что подтверждает хорошие аппроксимативные способности нечеткого персептрона. Система была протестирована на данных приемо-сдаточных испытаний двигателя газоперекачивающих агрегатов. В этом случае оценка качества аппроксимации проводилась с использованием критерия согласия Колмогорова-Смирнова. Результаты анализа подтверждают высокую аппроксимативную способность нечеткого персептрона, подчеркивая его применимость в реальных приемо-сдаточных испытаниях.
Нейронные сети, нечеткие функции, аппроксимация, приемо-сдаточные испытания, c-means, нечеткий персептрон, плотность распределения вероятности
Короткий адрес: https://sciup.org/140303634
IDR: 140303634 | УДК: 004.89 | DOI: 10.18469/ikt.2023.21.2.09
Текст научной статьи Применение моделей искусственного интеллекта в приемо-сдаточных испытаниях
В современном мире статистические методы анализа данных являются важным шагом в научных исследованиях. Не умаляя достоинств теоретических методов исследования, значение экспериментальных методов трудно переоценить. Только с помощью эксперимента возможно получение достоверной информации об исследуемом объекте в реальном масштабе времени, после обработки которой возможно построение ее модели [1].
В различных научных исследованиях возникает необходимость определения параметров случайного процесса, дающих его исчерпывающее описание. На практике для их получения требуется решить задачу аппроксимации, позволяющую на основе имеющихся данных получить функцию, описывающую случайный процесс [2]. Задача аппроксимации плотности распределения вероятностей является важной, так как во многих прикладных задачах выдвигается гипотеза о распределении статистического ряда, которую необходимо проверить.
В данной работе рассматривается применение методов аппроксимации в задачах приемо-сдаточных испытаний.
Использование аппроксимации в данных задачах позволяет:
– анализировать данные для более точных оценок измерений, особенно в случае ограниченного набора данных или наличия шума;
– производить моделирование данных с целью прогнозирования поведения системы;
– уменьшить количество необходимых испытаний и измерений, что позволит сократить время и затраты на проведение приемо-сдаточных испытаний.
Обзор методов аппроксимации
Как показано в [3], методы аппроксимации можно разделить на два класса:
-
1. Параметрические методы аппроксимации.
-
2. Методы непараметрической статистики.
Применение методов из первой группы основано на гипотезе о конкретном виде функции плотности распределения. Для оценки параметров функции применяется, например, метод максимального правдоподобия [2]. Стоит отметить, что на практике бывает затруднительно проверить гипотезу о принадлежности выборки конкретному распределению, что делает невоз- можным применение методов параметрической аппроксимации.
Этого недостатка лишены методы второй группы. К ним можно отнести следующие алгоритмы [2]:
-
– аппроксимация сплайнами;
-
– аппроксимация ортогональными полиномами;
-
– ядерная оценка.
Общим недостатком этих оценок является то, что при построении модели не учитываются условия нормировки и неотрицательности полученной оценки. Это приводит к тому, что аппроксимирующее выражение может не являться плотностью распределения [4]. Также к недостаткам стоит отнести невозможность оценить параметры аппроксимируемой плотности.
Нейросетевая аппроксимация
Еще одним методом непараметрической статистики является использование нейронной сети в качестве универсального аппроксиматора. Корректность данной оценки следует из теоремы Хета-Нильсена о представимости любой многомерной функции нескольких переменных с помощью нейронной сети фиксированной размерности [5]. Таким образом, любую сложную функцию можно заменить более простой нейросетевой аппроксимацией, причем требуется только нелинейность функции активации нейрона.
Аппроксимирующие нейронные сети обладают целым рядом преимуществ по сравнению с другими способами аппроксимации:
– нейронные алгоритмы имеют потенциал для распараллеливания процесса обработки информации одновременно между всеми нейронами, что приводит к многократному ускорению работы нейронной сети;
– благодаря большому количеству нейросетевых соединений, сеть становится нечувствительной к ошибкам, возникающим в отдельных нейронах в процессе аппроксимации;
– нейросетевые модели позволяют добиться меньшей ошибки аппроксимации по сравнению с другими методами непараметрической статистики [4];
– оценка плотности вероятности является более гладкой, чем при использовании сплайнов и ортогональных полиномов.
Однако нейронные сети также не лишены ряда недостатков. Во-первых, для них также не выполняются условия нормировки и неотрица- тельности. Во-вторых, аппроксимирующее выражение является в разы более сложным, чем при использовании полиномов.
Также для получения качественной модели необходимо подобрать параметры нейронной сети, что является сугубо эвристическим действием, не зависящим от определенной математической формулы.
Подготовка данных
Для построения оценки плотности распределения вероятности необходимо произвести первичное оценивание, построив гистограмму наблюдаемого статисти чес кого ряда, и выделить на ней точки { x i , y. }, i = 1, M , где M - число дифференциальных коридоров гистограммы, которые и будут входить в выборку данных. Для построения гистограммы в данной работе используется алгоритм, предложенный в [2].
В процессе обучения и работы на вход нейронной сети подается значение, равное координате середины интервала гистограммы плотности вероятности, а на выходе сети должно получиться значение, соответствующее ординате гистограммы в данной точке.
Нечеткий персептрон
В данной работе для решения задачи аппроксимации предлагается использовать модель нечеткого персептрона. Для данного типа сети сформулирована теоремы об универсальной аппроксимации, которая утверждает, что любая непрерывная функция на замкнутом интервале может быть представлена сходящимся рядом полиномов [5].
В случае нечеткого персептрона достаточно одного скрытого слоя для построения равномерной аппроксимации с заданной точностью для любого обучающего множества, представленного набором обучающих пар. Однако теорема не утверждает, что использование одного скрытого слоя дает оптимальные результаты в плане сходимости и скорости работы алгоритма.
Структура нечеткого персептрона, представленная на рисунке 1, является гибридной и объединяет в себе сеть с нечеткой организацией и многослойный персептрон.
Использование гибридной архитектуры оправдано тем фактом, что при использовании гибридной сети задача разделяется на два независимых этапа, реализуемых отдельно друг от друга: этап фуззификации и этап работы многослойного персептрона (постпроцессора), приписывающего каждой группе кластеров соответствующий ей результат.
Многослойный персептрон
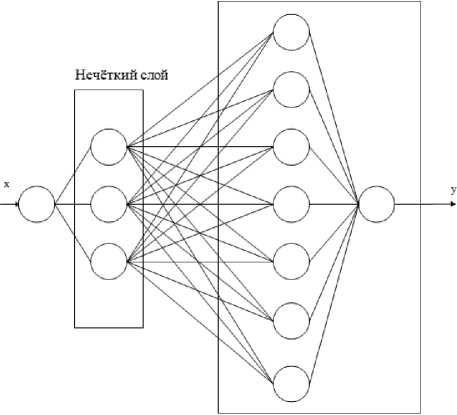
Рисунок 1. Структура нечеткого персептрона
Использование препроцессора, размерность которого больше размерности входного вектора, обосновывается теоремой Ковера о разделимости образов. В ней утверждается, что преобразование задачи классификации в пространство более высокой размерности повышает вероятность линейной разделимости образов. Это позволяет подавать на вход многослойного персептрона уже откластеризованные данные [6].
Постпроцессор в виде многослойного персептрона осуществляет перевод коэффициентов принадлежности точки множествам кластеризации в оценку плотности вероятности в данной точке.
Аппроксимирующее выражение для нечетко- го персептрона можно представить в виде:
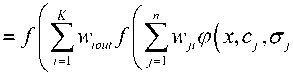
) , (1) л где K – количество нейронов в персептронном слое;
-
x – координата середины интервала гистограммы;
-
w iout , w ji – значения весов;
-
n – количество нечетких нейронов;
-
φ – нечеткая функция;
-
f – функция активации персептронного слоя;
C j , О j - значения параметров нечеткой функции.
Нечеткие функции
Ниже представлены нечеткие функции, используемые в данной работе.
Гауссова функция:
ф ( x, c, ст ) = exp
f ( x - c ) 2 )
l 2 ст 2 J
Функция Епанечникова [9]:
ф (x , c ст ) = 3 f l - ( x c ) J . (3)
4 1 ст )
Сигмоидальная функция:
ф ( x , c , ст ) =
П
exp
f ( x - c ) 2 l 2 ст2
+ exp
( x - c ) 2 ) 2 ст 2 J
Алгоритмы обучения нечеткого персептрона
Алгоритм обучения нечеткого персептрона носит двухэтапный характер. Первым этапом является определение параметров нечетких нейронов. После выполнения данного шага значения параметров замораживается и начинается обучение многослойного персептрона.
Обучение нечеткого персептрона требует определения центров нечеткой функции. В данной работе используется алгоритм C-Means [7]. Для некоторых функций также требуется параметр ширины. В разработанной системе для этого используется метод P-ближайших соседей [8].
Для обучения многослойного персептрона применялся алгоритм обратного распространения ошибки. Минимизировалась метрика MSE.
Исследование по аппроксимации плотностей распределения вероятностей
После обучения нейронной сети необходимо оценить качество полученного нейросетевого решения задачи аппроксимации.
С этой целью были сгенерированы временные ряды, подчиняющиеся заранее известным законам распределения вероятностей. Было проведено исследование по аппроксимации плотностей веро-
ятностей при помощи различных нечетких функций [10]. Качество аппроксимации оценивалось при помощи среднеквадратичного отклонения (СКО). Проводилась серия из 29 испытаний. В таблице 1 представлены максимальные значения СКО.
Тестирование проводилось на следующих параметрах нейронной сети:
– обучающие выборки построены по 10000 отсчетам;
– тестовая выборка с аналогичными характеристиками;
– коэффициент обучения – 0.03;
– функция активации многослойного персептрона – логистическая с параметром 5;
– число дифференциальных коридоров гистограммы – 15;
– число нейронов в нечетком слое – 12;
– число нейронов в многослойном персептроне – 15.
На основании данных из таблицы 1 мы можем сделать вывод, что нечеткий персептрон обладает хорошими аппроксимативными способностями. В среднем наилучшие результаты были получены при помощи нечеткой Гауссовой функции.
Исследование по аппроксимации плотностей распределения вероятностей данных приемо-сдаточных испытаний
Система была апробирована на данных приемо-сдаточных испытаний двигателя газоперекачивающих агрегатов. Так как распределение вероятности данных в данном случае нам неизвестно, для оценки качества аппроксимации использовался критерий согласия Колмогорова-Смирнова. Данный критерий используется для проверки гипотезы об однородности двух рассматриваемых выборок. В нашем случае сравниваются распределение вероятности реальных данных и выхода нейронной сети [11].
Для данной задачи использовалась конфигурация нейронной сети аналогичная той, что была
Таблица 1. Зависимость СКО аппроксимации нечетким персептроном от вида нечеткой функции
|
Нечеткая функция |
|||
|
Закон распределения вероятностей |
Гауссова функция |
Функция Епанечникова |
Сигмоидальная функция |
|
Нормальный |
0,0005 |
0,0268 |
0,0016 |
|
Экспоненциальный |
0,0026 |
0,0098 |
0,0045 |
|
Лапласа |
0,003 |
0,0163 |
0,0014 |
|
Вейбулла |
0,0009 |
0,0082 |
0,0025 |
|
Релэя |
0,0012 |
0,0084 |
0,0016 |
|
Арксинусоидальный |
0,0005 |
0,0011 |
0,0055 |
в прошлом эксперименте с нечеткой Гауссовой функцией.
Результаты анализа представлены на рисунках 2–4 и в таблице 2.
На основании полученных данных мы можем сделать вывод, что нечеткий персептрон обладает хорошими аппроксимативными способностями.
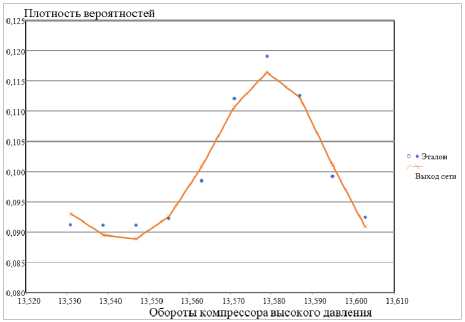
Рисунок 2. Сравнение эталона и выхода сети. Данные «Обороты компрессора высокого давления»
Таблица 2. Критерий Колмогорова-Смирнова для данных приемо-сдаточных испытаний
|
Данные |
Критерий Колмогорова-Смирнова |
|
Обороты компрессора высокого давления |
0.0003 |
|
Обороты компрессора низкого давления |
0.0007 |
|
Обороты свободной турбины |
0.0005 |
Заключение
В данной работе было описано использование нейросетевых методов в задачах аппроксимации плотностей распределения вероятностей. Были проведены эксперименты по подтверждению корректности результатов, а также исследование по выбору оптимальной нечеткой функции. Проведенные исследования показали корректность применения нечеткого персептрона в задачах аппроксимации.
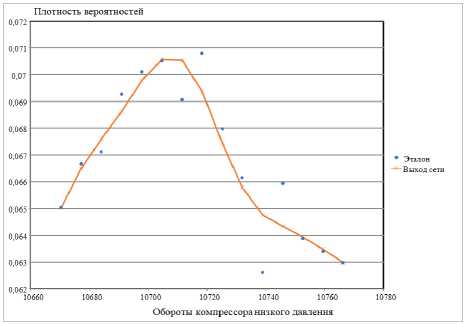
Рисунок 3. Сравнение эталона и выхода сети. Данные «Обороты компрессора низкого давления»
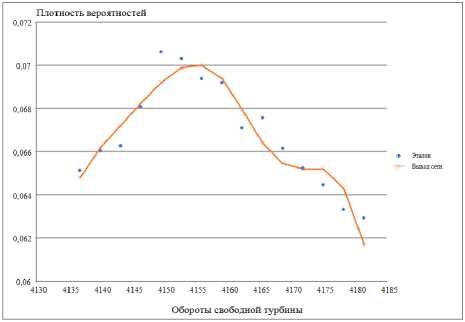
Рисунок 4. Сравнение эталона и выхода сети. Данные «Обороты свободной турбины»
Список литературы Применение моделей искусственного интеллекта в приемо-сдаточных испытаниях
- Прохоров С.А., Куликовских И.М. Численные методы, алгоритмы и комплексы программ для проведения вычислительного и натурного экспериментов. Самара: Инсома-пресс, 2019. 208 с.
- Прохоров С.А. Аппроксимативный анализ случайных процессов. Самара: СНЦ РАН, 2001. 380 с.
- Терехов С.А. Нейросетевые аппроксимации плотности распределения вероятности в задачах информационного моделирования // Нейроинформатика–2002: материалы Всероссийской научно-технической конференции. М.: МИФИ, 2002. С. 94–120.
- Лезина И.В. Аппроксимативный анализ законов распределения ортогональными полиномами и нейросетевыми моделями: дис. … канд. техн. наук. Самара, 2012. 108 с.
- Хайкин С. Нейронные сети: 2-е изд., исправленное; пер. с англ. М.: ООО «И.Д. Вильямс», 2006. 1104 c.
- Осовский С. Нейронные сети для обработки информации / пер. с польск. И.Д. Рудинского. М.: Финансы и статистика, 2002. 344 с.
- Bezdek J.C., Ehrlich R., Full W. FCM: The fuzzy c-means clustering algorithm // Computers and geosciences. 1984. Vol.10, no. 2–3. P. 191–203.
- Tarasenko L. Supervised and unsupervised learning in radial basis function classifiers // IEEE Proceedings – Vision, Image and Signal Processing. 1994. no. 4. P. 210–216.
- Дьерфи Л., Деврой Л. Непараметрическое оценивание плотности. L1-Подход / пер с англ. А.Б. Цыбакова. М.: Мир, 1988, 408 с.
- Тарасов А.А., Лезина И.В. Исследование аппроксимативных возможностей нечеткого персептрона при использовании различных ядерных функций // Перспективные информационные технологии (ПИТ–2020): материалы международной научно-технической конференции. Самара: Изд-во СНЦ РАН, 2020. C. 61–63.
- Колмогоров А.Н. Теория вероятностей и математическая статистика. М.: Наука, 1986. 535 с.


