Применение модели авторегрессии и скользящего среднего для спектрального оценивания в Фурье-спектроскопии

Кп) - отсчеты регистрируемой интерферограммы с оптической разностью хода, равной nh;

h - шаг дискретизации интерферограммы;

v - волновое число на интервале [0z 1/2h].

Конечность интервала регистрации интерферограммы по оптической разности хода позволяет в этом случае получить лишь некоторую оценку спектра

S(v) = h £ I (n) exp>(-i2jtvnh), n=~” где

I(n) =■ I(n)' |n,5N 0 , lnl>N,

N - число зарегистрированных отсчетов интерферограммы;

N=L/h;

L - предел изменения оптической разности хода в интерферометре в процессе указанной регистрации.

Эта оценка §(v) ограничена по спектральному разрешению соответствующей аппаратной функцией прибора (ширина которой обратно пропорциональна величине L) . В свою очередь наличие боковых лепестков аппаратной функции приводит к частичному перетеканию энергии каждой спектральной гармоники в указанные лепестки, то есть к дополнительному искажению спектра; Для уменьшения спектральных искажений, обусловленных боковыми лепестками аппаратной функции, интерферограмму аподизи-руют, то есть умножают на А(п) - некоторую весовую функцию.

Соотв ет с т вен но

$ (v) = h 2 A(n)T(n)exp(-i2nvnh).

П = -оо

К сожалению, в этом случае за уменьшение величины вторичных лепестков приходится платить увеличением ширины аппаратной функции.

До настоящего времени увеличения спектрального разрешения в Фурье-спектроскопии добивались практически лишь путем увеличения пределов изменения оптической разности хода в интерферометре, что позволяло уменьшить ширину аппаратной функции прибора. Разработчики шли по пути усложнения приборов, что сопровождалось увеличением их габаритов и стоимости.

В действительности об исследуемом процессе имеется, как правило, достаточно много информации и можно сделать более разумные предположения, чем равенство нулю значений интерферограммы вне регистрируемого интервала. Использование такой информации позволяет выбрать модель, хорошо аппроксимирующую реальный процесс, и с помощью определения параметров модели по результатам измерений получить более точную спектральную оценку, не прибегая к увеличению пределов изменения оптической разности хода.

Одним из возможных подходов к решению этой задачи является использование модели авторегрессии и скользящего среднего (АРСС) исследуемого процесса, описываемой следующим рекуррентным соотношением [з]:

Х(п) * 2 а^ХСп —k) =  2 biE(n-L)z                                         ^^

к=1             1=о где

Х(п) - дискретный стохастический процесс;

Е<п) - "белый" шум с нулевым средним и дисперсией л2?

р, q - порядки авторегрессивной (АР) и скользящего среднего (СО частей процесса;

а^, Ь[ - действительные константы.

Спектральная плотность мощности процесса (1) может быть записана [3] как

S(y) = n2h	q 2 b^exp(-i 2nyhI) L = o	2 •                                                   (2)
	p 1+2 3|texp(-i 2rcvhk) k = i

Таким образом, в рамках предлагаемой модели спектр может быть восстановлен по конечному числу параметров (л², а(к = 1,...р), b l (L=O_Z.. .q)) .

Для обоснования выбора модели (1) для оценивания спектра в Фурье-спектроскопии заметим, что АРСС процесс является регулярным процессом, удовлетворяющим условию Пэли-Винера [4]

1 /2 h Г I I nS(v) Idy <«. -1/2h

Известно [5] , что регулярный процесс является реакцией физически осуществимого фильтра, на вход которого подается стандартная некоррелированная последовательность .

Фильтр называется физически осуществимым (каузальным), если его импульсная переходная характеристика h(t) удовлетворяет условию

h(t)=O, t<0.                                                                 (3>

В спектрометре исследуемый образец освещается излучением от широкополосного источника, спектр излучения которого близок (в рабочем диапазоне) к спектру '•белого1' шума. Следовательно, исследуемый образец можно считать каузальным фильтром, порождающим АРСС процесс.

Определим автокорреляционную функцию KL) процесса (1). С учетом (3) она примет вид

Р                   Я

• -Е a_kI(L-k) ♦ Е b_kI k=i               k = L

Р

• -В a_kI(l-k)_z k = i

FV(l-k), IllSq

G *

I I l>q

(4а)

где I^^(l) - функция взаимной корреляции процесса Х(п) и шума £(п).

Подсистему (4б) называют уравнениями Юла-Уокера. Параметры ак являются решениями этой подсистемы. Из (4б) видно, что неизвестные отсчеты автокорреляционной функции представляются в виде линейной комбинации р ее предыдущих отсчетов (в отличие от традиционного Фурье-анализа, когда неизвестные отсчеты принимаются равными нулю).

что

Преобразуем выражение (2)

3^=0 при к<0 и к>р

и

bL=0

к более удобному виду. Считая aQ«1 и учитывая, при КО и Kq получим

где

P

E akexp(-i2nvhk) k = o

P

E m=-p

Amexp(-i 2n-vhm)

*m

P

E a^a,,   ;

k=o k k-m

q

Е

L = о

b[exp(-i 2nvhD

q

S B^exp(-i2nvhm) m = -q

где

в; = = btbL_m.

l=o

Пусть Bm=T|2hB^, тогда с учетом четности функций Am и Bm получим q

E Bmcos(2nvhm)

S(v) = —-------------- •                                                  (6)

E Amcos(2nvhm) m=o

Коэффициенты Bm найдем, умножив обе части последнего выражения на знамена тель правой части и выполнив преобразование Фурье:

Р

Вщ =  2 AnI(m-n).                                                             (у)

п=-р

Как видим, при использовании выражения (6) для восстановления спектра нет необходимости определять параметры и3 и Ь[. Точность же спектральной оценки зависит от точности определения параметров ак.

Реальный сигнал, снимаемый с Фурье-спектрометра, всегда зашумлен. Основным источником шумов в ИК диапазоне является тепловой шум приемника излучения. Этот шум хорошо описывается распределением Гаусса с нулевым средним и некоторой дисперсией а3. Без ограничения общности будем считать шум белым (в случае его коррелированное™ можно применить декоррелирующее преобразование). Дисперсия шума может быть измерена до проведения основного эксперимента.

Определим отсчеты интерферограммы как

I(i>=1 *(i)-Е(i)z                                                                                    <8)

где

I*(i) - идеальные значения автокорреляционной функции;

е(1) - значения шума, удовлетворяющие условиям:

М{е(1)}=0, M(e(i)³}=0³, М {е (i )е( j )} =0 при iNj.

С учетом (8) система уравнений (46) примет вид рР

I(L) + Е ак1(1-к) = e(l) + Е aL.e(l-k)z ILI>q.(9)

к=1к=1

Пусть L меняется от q + 1 до q+t, где t>p .

Введем обозначение: Р

V(I) = е( I) ♦ Е а_кЕ(1-к) к = 1

и перепишем систему (9) в матричном виде

T+la=Vz                                                                    <10)

где

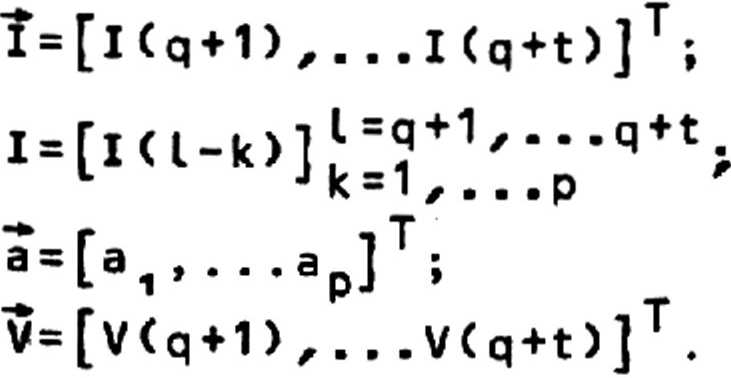
Вектор V распределен по нормальному закону, поскольку каждая его компонента является линейной комбинацией гауссовых случайных величин. Очевидно, что M(V)=5.

Найдем корреляционную матрицу вектора V

Р

Введем обозначение

G(a) - [6Ck-D ♦ a|k_t| + Да^к-ц^к,^.,,...^

Тогда корреляционная матрица вектора V запишется в виде

C*=aaG(a).                                                             (и)

В работе [6] описано использование авторегрессионной модели для отыскания спектра электронно-циклотронного излучения плазмы.

Но подобная модель соответствует довольно узкому классу спектров. Известно [3] , что АР модель хорошо описывает пики, а СС модель - провалы в спектрах. Объединение этих моделей позволяет существенно расширить класс восстанавливаемых спектров, что продемонстрировано на рисунках 1-3-

На рис. 1 представлен модельный спектр (с характерными для спектроскопии Формами линий, а именно, гауссовой, лоренцевой и их суперпозицией), на основе которого синтезировалась исходная интерферограмма. Восстановленный из нее с помощью АРСС модели спектр хорошо, как видно из рис. 2, согласуется с исходным (получить приемлемый результат с помощью АР модели не удалось). На рис. 3 представлен для сравнения спектр, восстановленный с помощью традиционного метода Фурье-анализа (с использованием эффективной аподизации) по тому же числу отсчетов интерферограммы, что и в случае применения АРСС модели. Очевидно, что спектр, показанный на рис. 2, гораздо ближе к исходному, чем спектр, показанный на рис . 3.

Перейдем теперь к анализу метода при зашумленной интерферограмме. В уже упоминавшейся работе [6] для нахождения вектора параметров а авторы использовали классический метод наименьших квадратов, без учета зашумленности матрицы I. В результате оценка оказывается смещенной. Опыты на моделях показали, что при таком способе решения задачи не удается получить устойчивую спектральную оценку. Воспользуемся для оценивания параметров методом наибольшего правдоподобия. Как известно, этот метод позволяет получить асимптотически несмещенную, эффективную оценку.

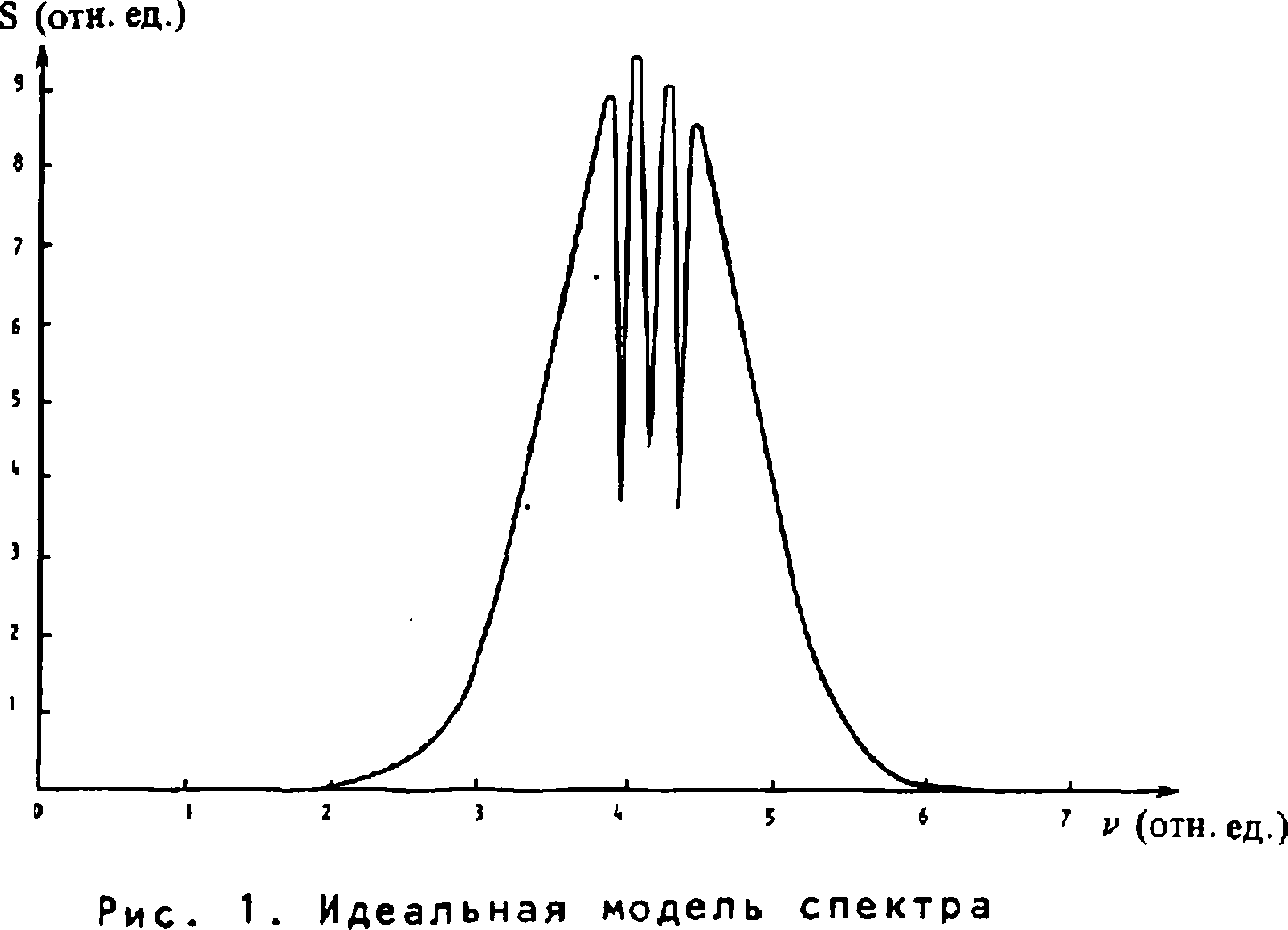
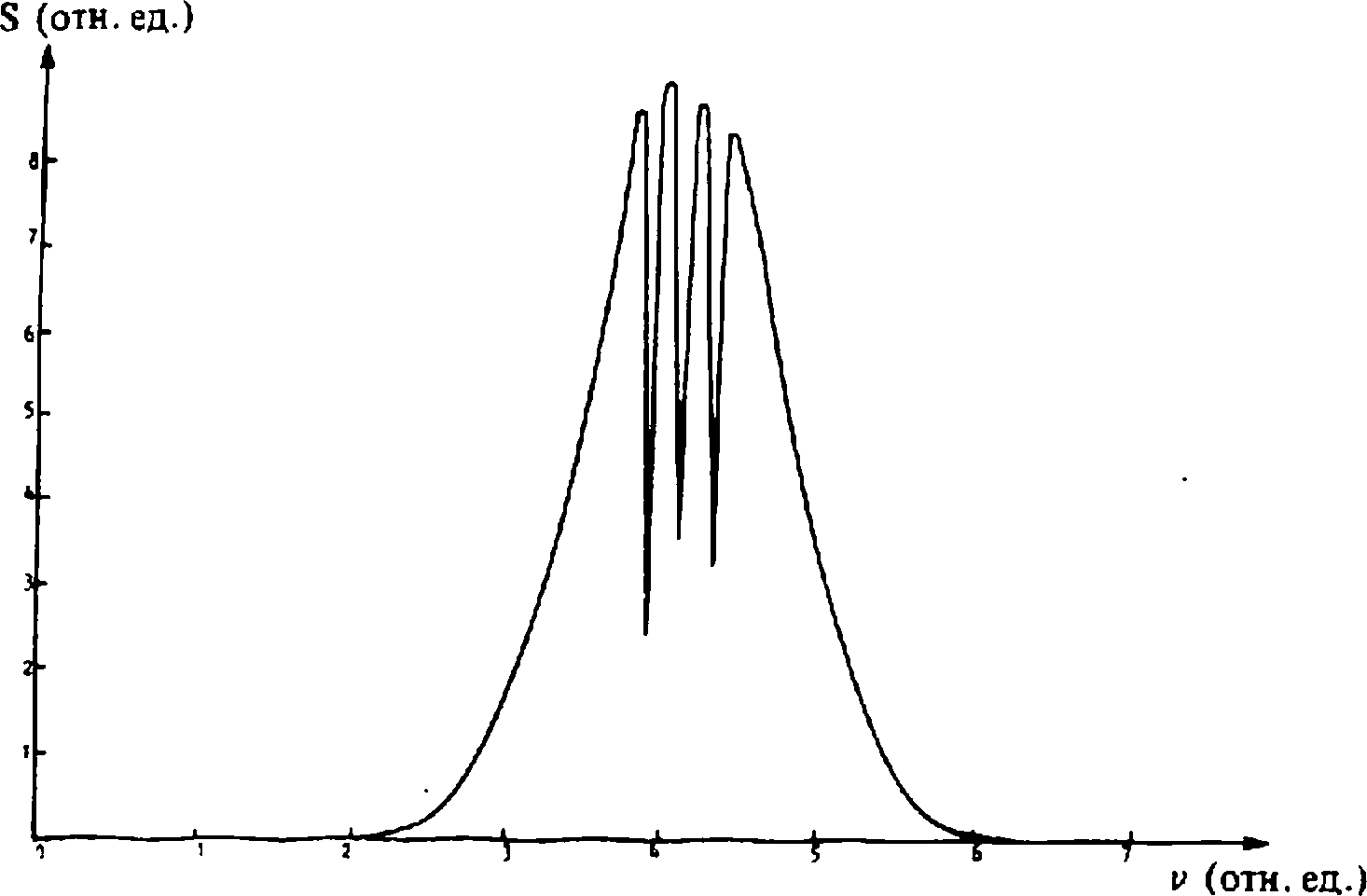
Рис. 2. АРСС оценка спектра. Порядок р АР части - 21, порядок q СС части - 70.

Число использованных точек интерферограммы - 92

S (отн. ед.)

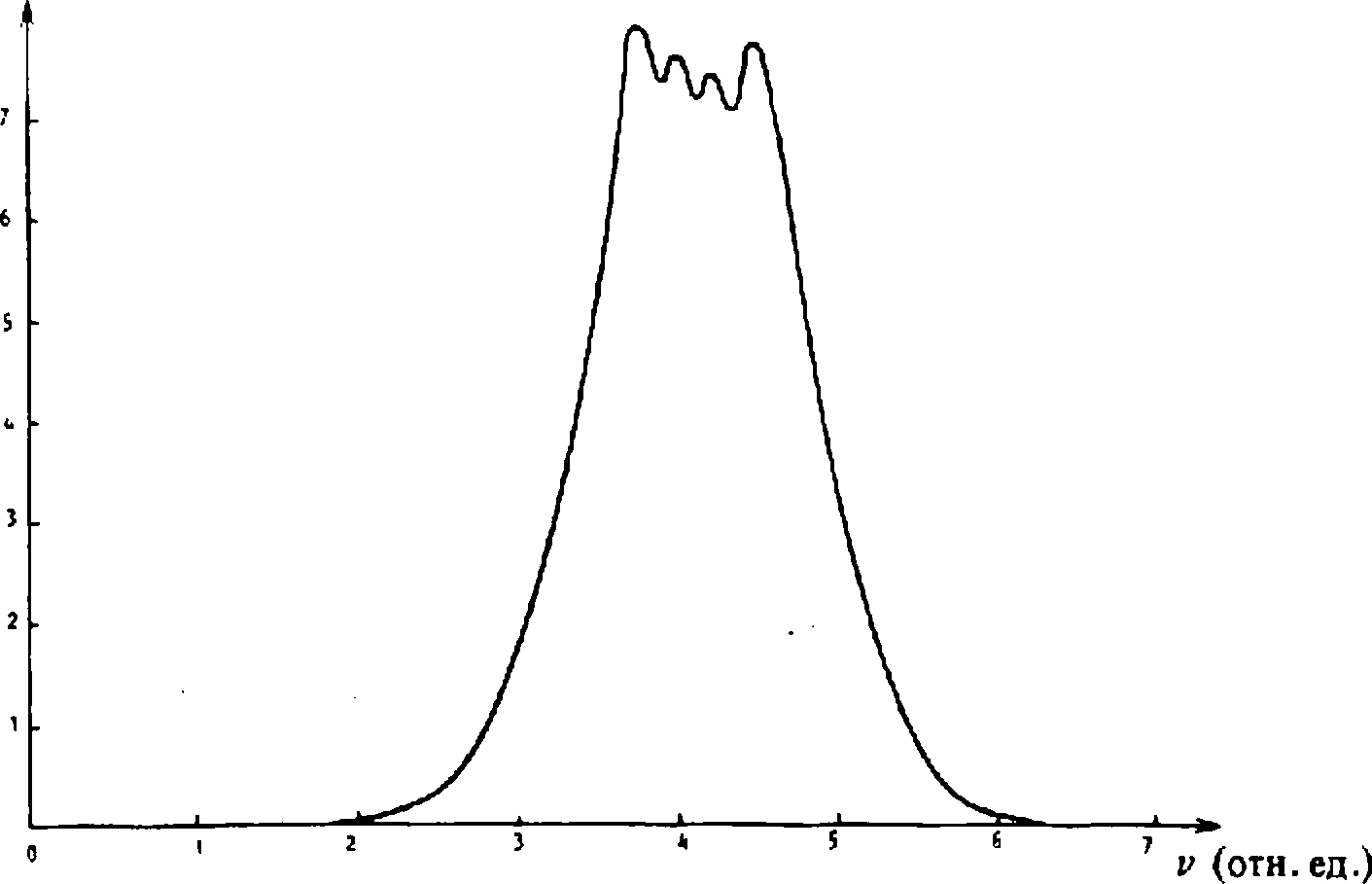
Рис. 3. Оценка спектра, полученная традиционным методом Фурье-анализа по 92 точкам интерферограммы

Запишем функцию правдоподобия для вектора V. Поскольку V распределен по нормальному закону, то с учетом (10) и (11) эта функция примет следующий вид:

P(V/az р) = -------L--------— ехр{--—(T+Ia)TG(a)-1(T+Ia)}z (гда2)^ IG(a)|l/a        2а2

где lG(a)| - определитель матрицы G(a)z р - порядок АР части процесса.

Для нахождения параметров необходимо максимизировать по параметрам лога рифмическую функцию правдоподобия:

Ln P(V/a

|ln(2ito2) - ^Ln|G(a) |--L(T+ia)TG(a)-1

Максимизация последнего выражения эквивалентна минимизации следующего функ- ционалa:

ф(7/ау p) = Ln|G(a)| + — (T+Ia)G(a)~1(T+Ia).                             (13)

Поскольку функционал нелинеен, то для решения задачи необходимо использовать методы поиска глобального экстремума. Такой подход для оценивания параметров может быть использован в случае быстротекущих процессов. (Например, в задаче, описанной в [6], спектр электронно-циклотронного излучения плазмы гладкий и имеет колоколообразную форму. Соответственно порядок р описывающего его АР процесса невелик, что облегчает минимизацию (13)).

Если свойства исследуемого образца не меняются во времени, можно использовать режим многократной регистрации интерферограмм. При этом задача существенно упрощается .

Пусть I k (i ) * к-я реализация интерферограммы, а £^=(1) - шум к-й реализации. Тогда система (9) примет вид:

рР

I (L) + Е akIk(l-k) = е0С1) + S ak£k(l-k)z |L|>q.(П

°       к=1к=1

Найдем корреляционную матрицу вектора V, каждая компонента которого в дан ном случае описывается выражением: р

V(l) = e0(L) + Е akek

Поскольку И {eiCk)ejс I)}-о при i^j (разные реализации шума статистически независимы)# а также М (е^(к)еj(I)}=0 при к^1 получим

Р

С.. .. = аа5(к-1)(1 ♦ Б а?)

IK-LI                    j=1 j или

^ = o^l ♦ 5Ta)Etxt, где Etxt * единичная матрица размерности txt. Другими словами, V - гауссов нбе-лый" шум с нулевым средним и дисперсией о2 ( 1 + a^£) е

Обратим внимание на то, что система (14) использует не всю имеющуюся у нас информацию. Из N реализаций интерферограммы можно составить N систем уравнений вида р _             _

Im( I) ♦ Е akIk(l-k) = e^d) +

0           k = i где

Р

Е аьЕ™(1-к), H1>qz m=Oz...N-1, К>р,

ijd-k) к

(1-к) N

е"(1-к) к

= e

(1-к); N

k=0,eeeZPZ m=0z,e,zN*1.

Поскольку шумы разных реализаций статистически независимы, то независимы и системы (15). Построим среднюю логарифмическую функцию правдоподобия для векто-ров Vm с компонентами

— Р

Vmd) = e"(L) + Е akEkd-k)z m = 0z.. .ZN-1. k = i

Эта функция будет иметь вид

N-t          _

Е <Г_тл 1,а)'<Т, + 1,а)

+ в~°    ———=———— .        <16>

N 2                            2аа<1 + аТа>

Для нахождения оценки вектора параметров а нужно решить систему уравнений

^У^/ Р> = о, П = 1

Эап

В результате дифференцирования получим

N-1         N-1

Е l'l-а + Е IJ. ♦ Ntaaa m=o         m=o

Искомой оценкой будет такой

n-i__t. -т ^N"¹ т* -tⁿ'¹ т -Е lit, * 2а^т Е i;i„ ♦ .а Е I„I_ma m = o______________m = o____________m=o

- la достигает

1 + ^a вектор а, при котором выражение (16)

глобального максимума.

Неизвестным остался порядок р авторегрессионной масти АРСС процесса» Его нельзя определить по методу наибольшего правдоподобия, поскольку изменение по* рядка меняет вид плотности распределения. Воспользуемся методом максимума энтро" пии [?] • Как известно, этот метод позволяет построить функцию распределения, наилумшим образом удовлетворяющую экспериментальным данным.

Выражение (16) является естественной оценкой математического ожидания логарифмической функции наибольшего правдоподобия, которое задается выражением

R(e0, е) = /.../f

где

в - [a »,..,ap, p]T - его оценка.

В работе [7] показано, что для произвольных плотностей распределения f(x) и д(х) выполняется соотношение

-Г f(x)Ln g(x)dx>-/ f(x)Ln f(x)dx.                                     (18)

— oo                            —00

Причем эти выражения равны только при f(x)=g(x). Правая часть выражения (18) есть не что иное, как энтропия случайной величины х. В обозначениях (17) послед нее выражение перепишется как

-R(eo, e)>-R(60, 6О) = н(е0), где Н(60) - энтропия случайного вектора V.

Таким образом, выражение (16), взятое со знаком минус, является оценкой энтропии вектора V.

По определению [7] мерой энтропии случайного процесса называют предел нх - ^(^^...хг) при t-“.

В нашем случае оценкой меры энтропии будет величина

N-1         - т -

= dm ■♦ Im=>

Нх(в)

In 2nca(1 + a^) * —------------—------

N t a3(1 ♦ T a)

Известно [7], что мера энтропии "белого11 шума, распределенного по закону

Гаусса с дисперсией а3, определяется выражением

Hj = ^(Ln 2по3 + 1).

Этой величиной определяется мера энтропии случайного шума Е, наложенного на автокорреляционную функцию. Другими словами, выражение (20) определяет меру энтропии спектральной оценки, полученной традиционным методом Фурье-анализа. Сравнивая выражения (19) и (20), видим, что увеличение энтропии - это та цена, которую приходится платить за увеличение разрешения, то есть АРСС модель может эффективно использоваться для спектрального оценивания при небольших шумах.

Для определения порядка р может быть использован информационный критерий Акайке (ИКА) [8]z согласно которому выбирается такой порядок р, что минимально выражение

ИКА(р) = Hj(e) + p/t.                                                      (21)

Второе слагаемое в (20) отражает тот факт, что при увеличении порядка процесса увеличивается дисперсия оценки а. После определения оценки вектора параметров "а и порядка р АР части АРСС процесса могут быть найдены коэффициенты А_т (5)_z В_т (7) и оценка спектральной плотности мощности (6).

Реализация предложенного метода восстановления спектра будет представлена в последующих публикациях.