Применение модели EMMSP для прогнозирования доступных вычислительных ресурсов в кластерных системах

В области научных вычислений остро стоит вопрос рационального использования вычислительных ресурсов, поскольку сами ресурсы находятся в дефиците, а исследователи конкурируют за доступ к наиболее производительным окружениям. Под окружением мы подразумеваем не только сами вычислительные узлы, но и раз- Артамонов Юрий Сергеевич, ассистент кафедры информационных систем и технологий.

личную инфраструктуру – хранилища данных, сети, специальную периферию. Нередко разработчикам проекта доступно не одно окружение для запуска вычислительных задач, а несколько [1]. При наличии такого выбора, важно правильно оценить, в каком из окружений вычисления будут завершены раньше.

Подавляющее большинство современных кластеров и суперкомпьютеров используют пакетные системы для запуска задач, а это значит, что каждая задача перед своим запуском проходит через очередь пакетной системы. Пакетные системы занимаются планированием задач на основе политик выделения ресурсов кластера, чтобы обеспечить совместное использование дефицитных ресурсов пользователями. Время выполнения задачи в различных окружениях может быть сравнимым, если сами окружения имеют схожую производительность, но время, которое проводит задача в очереди, может отличаться очень сильно, поскольку оно зависит от загруженности окружения, количества задач в очереди и требований задачи [2]. Кроме того, время ожидания задачи в очереди может быть непредсказуемо для некоторых применяемых политик планирования задач.

Для прогнозирования объема доступных ресурсов требуются данные о загруженности вычислительных ресурсов и о профиле использования. Под профилем использования мы подразумеваем набор особенностей окружения, который может быть представлен историческими данными загрузки ресурсов [3]. При прогнозировании загрузки окружения важным является как большой массив исторических данных по исполнению задач, так и тренд загрузки ресурсов. На практике это означает, что данные загрузки нельзя описать одной конкретной математической моделью, и для прогнозирования потребуется использовать комбинацию моделей [4].

Приведем основные задачи прогнозирования, которые имеют прикладное значение в кластерных системах, предназначенных для запуска вычислительных задач.

• 1.    Прогноз момента запуска вычислительной задачи [5].

• 2.    Прогноз момента завершения вычислений задачи.

• 3.    Прогноз доступных вычислительных ресурсов окружения в некоторый момент времени в будущем.

• 4.    Прогноз появления задач с определенным уровнем требований к кластеру [6].

Метод решения этих задач сильно зависит от ограничения на общий объем вычислительных ресурсов. Ограничение на объем ресурсов бывает двух типов.

• 1.    Фиксированныйобъемвычислительных-ресурсов.

• 2.    Динамически изменяемый объем вычислительных ресурсов.

Фиксированный объем ресурсов характерен для кластеров и суперкомпьютеров, а примером случая с динамически изменяемыми вычислительными мощностями являются Desktop Grid [7]. Отказы оборудования нельзя рассматривать как ситуацию с динамически изменяемым объемом ресурсов, поскольку известен верхний предел доступных мощно- стей. В этой работе мы проанализируем применимость модели EMMSP для решения задачи прогнозирования загрузки вычислительных ресурсов с фиксированным объемом ресурсов и покажем ее достоинства, позволяющие задействовать ее в комбинации с другими моделями.

МОДЕЛЬ ПРОГНОЗИРОВАНИЯ EMMSP

Пусть задан временной ряд 7(1) = Z(1),Z(2),...,Z(T) . Наборпоследовательных значений Z^ = Z(t),Z(t + 1), ...,Z(t + M - 1),, лежащий внутри исходного временного ряда, назовем выборкой длины M с моментом начала отсчета t; м e {1, 2,...J),t E {1, 2, ..., T - M + 1} . Две выборки одинаковой длины, принадлежащие одному временному ряду, свяжем через параметр временной задержки k:

Z^ = Z^, ....Z^t + M - 1)

и

Z^ = Z(t - k), ...,Z(t-k + M- 1); к E {1,2,..., t - 1} В работе [8] сформулировано ключевое свойство выборок, позволяющее прогнозировать значения временных рядов по известным выборкам: фактические выборки временного ряда могут иметь подобие с будущими выборками.

Подобием двух выборок назовем их свойство, заключающееся в том, что одна выборка может быть выражена через другую с помощью линейной зависимости. Подобие выборок и его применение для прогнозирования временных рядов рассмотрено в работе [9], где автор приводит модель экстраполяции временных рядов по выборке максимального подобия (extrapol ationmodelonmostsimilarpattern, далее EMSSP) и доказывает ее применимость для задач прогнозирования.

Особенности модели EMSSP:

• -    модель относится к классу авторегрессионных моделей прогнозирования;

• -    модель работает со стационарными и нестационарными временными рядами;

• -    модель имеет один параметр M;

• -    экстраполяция значений временного ряда производится за одну итерацию.

Для применения модели EMMSP должны выполняться условия [10]:

• -    временной ряд должен быть равноотстоящим (значения процесса фиксироваться через равные интервалы времени) и относиться к классу рядов с длинной памятью;

• -    задача прогнозирования на P значений вперед – относиться к классу краткосрочного или среднесрочного прогнозирования данного типа временного ряда;

• -    длина исходного временного ряда – составлять не менее 500 P – 700 P .

ПРИМЕНЕНИЕ МОДЕЛИ EMMSP ДЛЯ ПРОГНОЗИРОВАНИЯ ЗАГРУЗКИ РЕСУРСОВ КЛАСТЕРА «СЕРГЕЙ КОРОЛЁВ»

В рамках веб-сервиса Templet [11] была собрана статистика исполнения задач на кластере «Сергей Королёв» с ноября 2013 г. по май 2016.

При помощи модели EMMSP было организовано непрерывное прогнозирование загрузки кластера в системе Templet Web (http://templet. . Кластер «Сергей Королёв» (http:// ru) имеет гетерогенную структуру и включает в себя узлы нескольких типов, разбитые на группы по типу узла. Задача состояла в прогнозировании количества занятых узлов кластера в нескольких наиболее интенсивно используемых группах узлов. Целевое время прогноза – 12 часов, при этом требовалось спрогнозировать 12 значений временного ряда, по одному среднему значению занятых узлов в группе на один час. Для обучения и прогнозирования загрузки были выбраны данные по группам узлов qdr_tmp (рис. 1) и ddr_tmp. Их загрузка представляет наибольший интерес в связи с большой регулярной загрузкой.

Модель EMMSP была выбрана исходя из нескольких особенностей данных загрузки кластера:

• -    временные ряды являются нестационарными;

• -    в данных есть периодические составляющие, соответствующие большому количеству периодических событий;

• -    есть участки, изменения на которых имеют взрывной характер;

• -    результаты прогнозирования хорошо поддаются интерпретации, что позволяет принимать на их основе решения по управлению кластером;

• -    в результате прогнозирования известно,

вышли ли данные за границы применимости модели, что позволяет комбинировать эту модель с другими моделями.

Пример прогнозирования данных загрузки кластера приведен на рис. 2. Пунктиром показаны прогнозные значения ряда. График прогнозных значений был получен вычислением прогноза через каждые 12 точек. На графике можно видеть 2 выброса, которые соответствуют моментам выхода данных за границы применимости модели EMMSP.

При обучении модели EMMSP программный комплекс TempletWeb обнаруживает подобные выборки во временных рядах и собирает статистику по ним для ретроспективного анализа. Примеры подобных выборок длины 40 точек приведены на рис. 3.

В процессе обучения выбирается наиболее эффективная ширина окна подобной истории (параметр модели M ), которая затем используется для прогноза. Для каждой ширины окна поиска истории вычисляется среднеквадратичная ошибка, которая учитывается при выборе наиболее эффективного окна. График среднеквадратичной ошибки прогноза в зависимости от ширины окна поиска подобных выборок истории приведен на рис. 4.

Распределение средней ошибки прогноза при помощи модели EMMSP близко к нормальному, гистограмма распределения средней ошибки представлена на рис. 5. Модель дает среднюю абсолютную ошибку 8,7 узлов при максимальном числе узлов в группе 70.

В качестве итоговой метрики ошибок выбрана средняя абсолютная ошибка (MAE, формула 1), поскольку средняя абсолютная ошибка в процентах (MAPE) не может быть использована в рядах, включающих значения близкие или равные 0.

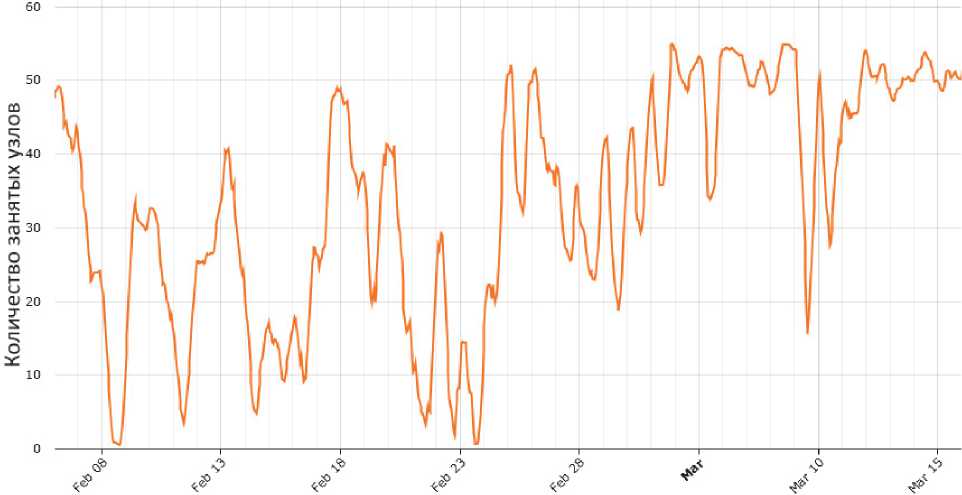
Рис. 1. График количества занятых узлов группы qdr_tmp кластера «Сергей Королёв»

Количество занятых узлов

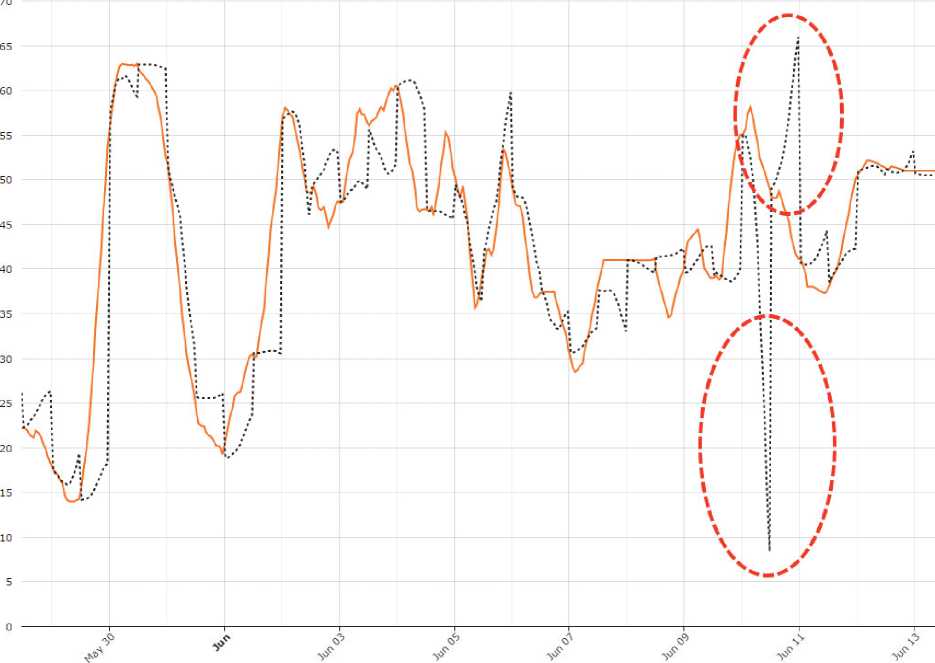
Рис. 2. Прогноз загрузки ресурсов кластера «Сергей Королёв» при помощи модели EMMSP

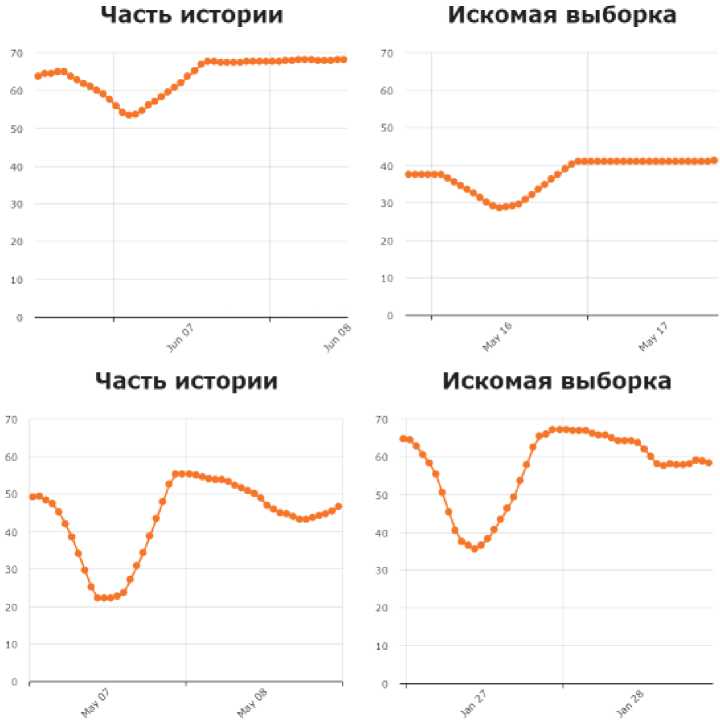
Рис. 3. Примеры подобных выборок, выявленные моделью EMMSP

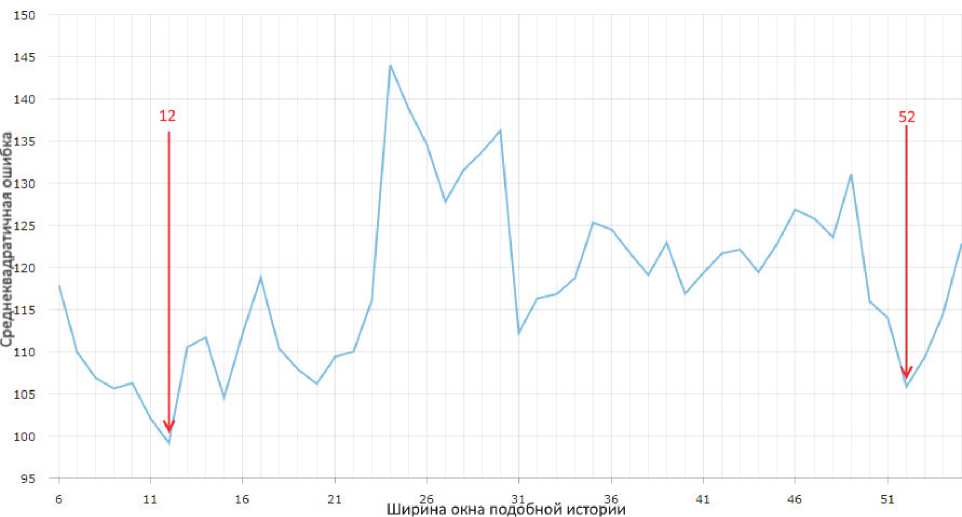
Рис. 4. График ошибки MSE в зависимости от ширины окна подобия

N

мае- ^|z(O-z(t)|, (1) t=i

Модель работает на данных загрузки кластера, но не настолько хорошо, чтобы применять ее без подкрепления результатами другой модели. Например, эту модель можно применять в комбинации с наивным прогнозом путем сдвига текущих значений ряда. Комбинацию моделей можно построить по эмпирическому правилу: если множитель подобия выборки выходит за границы отрезка [0.1, 5.0], то использовать сдвиг. На рис. 6 представлен график загрузки узлов с фактическими и прогнозными (пунктирная линия) значениями. Один из участков, на котором лучший результат показывает модель прогнозирования по выборке наибольшего подобия помечен как EMMSP, а пример участка, на котором выполняется сдвиг, помечен как SHIFT.

При использовании такой комбинации моделей ошибка MAE для группы с максимальным числом узлов снижается до значения 6,9. Если же рассчитать среднюю абсолютную ошибку только для участков, на которых модель EMMSP применима (значение множителя подобия попадает в отрезок [0.1, 5.0]), то MAE составит 5,2.

По результатам тестирования модели мы можем сделать вывод о том, что модель хорошо себя показывает только на некоторых участках, и ее можно применять в комбинациях моделей путем адаптивной селекции или композиции [12]. При этом результаты, которые дает модель, могут быть легко интерпретированы, что позволяет принимать на их основе управленческие решения по выбору окружения или развитию кластера. Это качество выгодно отличает модель EMMSP от моделей на основе нейронных сетей и других моделей машинного обучения, построенных по принципу черного ящика.

Алгоритм прогнозирования интегрирован в сервис TempletWeb, что дает пользователям возможность оценить время запуска задачи.

ПРИМЕНЕНИЕРЕЗУЛЬТАТОВ ПРОГНОЗИРОВАНИЯ

Результаты прогнозирования доступных ресурсов и момента запуска отдельных задач можно применять для решения задач планирования:

• -    выбора окружения для запуска задачи пользователя: обеспечить быстрый запуск, если задача интерактивная, или быстрое получение результатов;

• -    построения плана размещения компонентов распределенного приложения, если требуется построить распределенный конвейер вычислений;

• -    оптимизации параметров запуска и объемов входных данных для минимизации общего времени обработки;

• -    снижения энергопотребления кластеров и центров обработки данных, когда ресурсы не используются;

• -    увеличения парка серверов для облачных окружений, если загрузка ресурсов облака постоянно растет;

• -    планирования периодов обслуживания серверов кластера.

С развитием облачных технологий вопросы энергоэффективности ресурсов выходят на первый план. Прогноз загрузки вычислительных ресурсов облака позволил бы отключать некоторое количество неиспользуемых ресурсов и выявлять необходимость пополнения парка машин в случае роста загрузки.

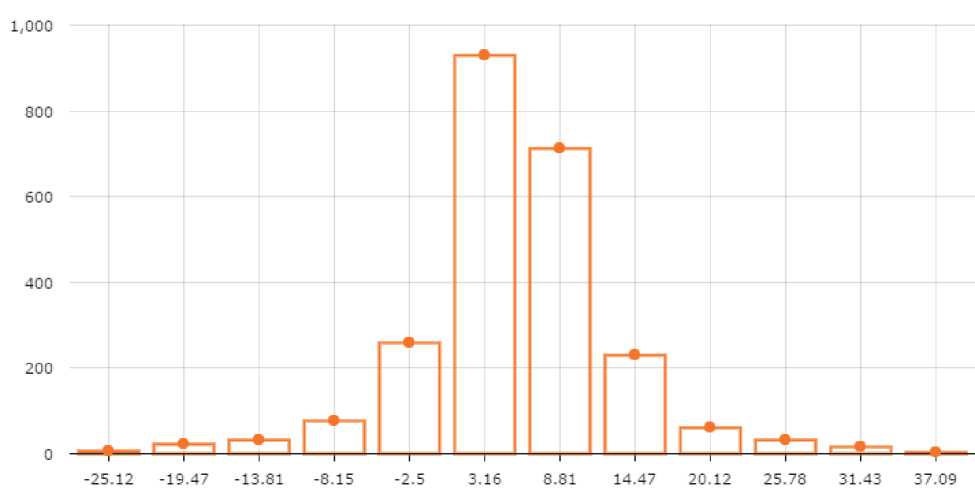
Рис. 5. Распределение средней абсолютной ошибки прогноза

Количество занятых узлов

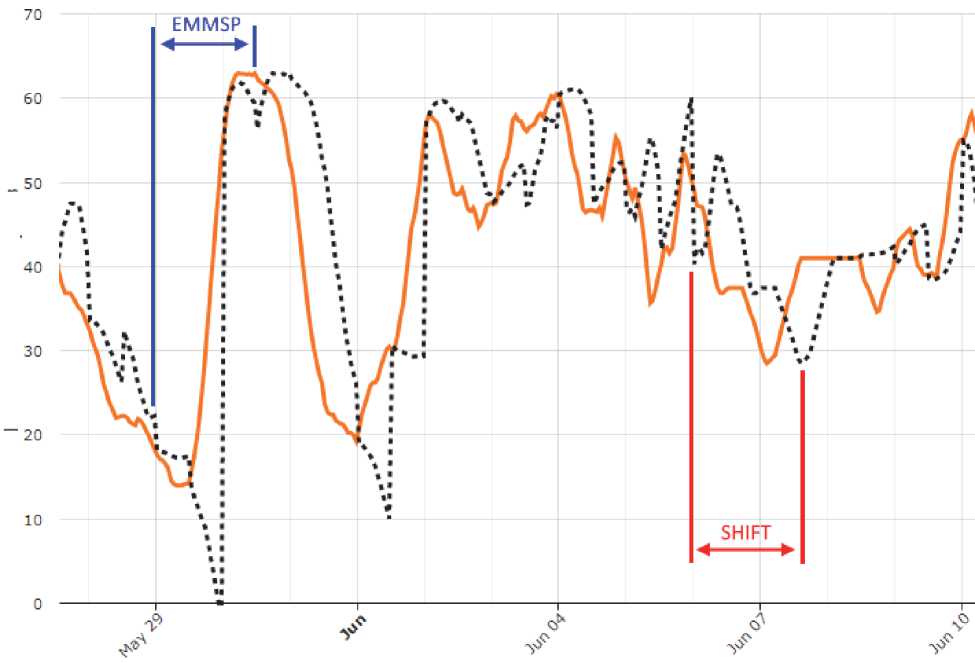
Рис. 6. График прогнозных значений загрузки кластера для прогноза комбинацией моделей EMMSP и наивного прогноза