Применение модели Хольта - Винтерса для прогнозирования работоспособности серверных систем

Увеличение стоимости серверных систем, существенная зависимость организаций от эффективности работы серверов, повышение требований к бесперебойности делают актуальной задачу обеспечения работоспособного состояния корпоративных серверов. Под сервером понимается программно-аппаратный комплекс, предоставляющий клиентам доступ к определенным ресурсам или службам [11]. Для обеспечения раннего пред-

36 в ыпуск 4/2019

упреждения специалиста, ответственного за работоспособность серверной инфраструктуры, о возможных нарушениях в функционировании серверов необходимо применять методы анализа состояния объектов, ориентированные как на текущие, так и на прогнозные тенденции изменения параметров серверов.

Для прогнозирования работоспособности серверных систем следует собрать статистическую информацию о работе объектов. Собранные статистические данные о каждом параметре сервера представляют собой временные ряды. В общем виде модель временного ряда выглядит следующим образом: X ( t ) = T + S + E для аддитивной мо дел и или X ( t ) = TSE для мультипликативной модели временного ряда, где t =1, n ; T – тренд; S – сезонная компонента; E – случайная компонента [3].

Пусть X , X , ..., X_N – N технических параметров сервера, характеризующих его работоспособность. Тогда состояние сервера S ( t ) в момент времени t описывается перечнем значений его параметров:

S ( t ) = ( x ₁( t ), x ₂( t ), ..., x_N ( t )). (1)

Значения ка ждого параметра сервера x_i , i =1, N , известные в дискретные моменты времени t =1, T , представляют собой временной ряд X_i ( t ) = ( X_i (1), X_i (2), ..., X_i ( T )). Для решения задачи прогнозирования параметров сервера необходимо найти функциональную зависимость между временным рядом X_i ( t ) и будущим прогнозируемым значением X ˆ _i(T + k) [2]:

X ( T + k ) = F ( X i ( T ), X i ( T - 1),..., X i ( T - p ) ) , (2) где k – интервал прогноза; p – глубина погружения временного ряда.

Материалы и методы

На данный момент существует более двадцати различных моделей и соответствующих им методов прогнозирования временных рядов [4]. Выбор модели должен базироваться на особенностях анализируемых временных рядов и специфике решаемой задачи.

Для лица, ответственного за работоспособность сервера, больший интерес представляет краткосрочный прогноз (минуты или часы) для оперативного детектирования поведения рядов, не соответствующих прошлой истории. Долгосрочные прогнозы (недели или месяцы) представляют меньший интерес, поскольку можно ожидать, что временные ряды будут развиваться в динамичной среде.

Сервер состоит из множества подсистем, параметры каждой из которых необходимо фиксировать и прогнозировать для получения полноценной информации о работоспособности сервера.

Временные ряды, характеризующие параметры сервера, могут быть описаны изменяющимися трендами при планомерном увеличении или уменьшении потребностей в ресурсах сервера. Также возможно присутствие сезонной составляющей при регулярном и повторяющемся обращении к ресурсам сервера. Таким образом, временные ряды серверных систем не являются стационарными, а модель должна учитывать тренд и сезонную составляющую ряда.

Распространенными моделями прогнозирования временных рядов являются: авторегрессионные модели; модели экспоненциального сглаживания; нейронные сети [Там же].

Дубровин М.Г., Глухих И.Н. Применение модели Хольта – Винтерса... 37

Использование модификации авторегрессионной модели, учитывающей сезонную составляющую ряда (SARIMA), показывает хорошие результаты в прогнозировании нагрузки серверных систем [7]. Согласно методологии Бокса – Дженкинса [5], если исходный ряд не является стационарным, то его необходимо привести к стационарному виду для использования данной модели. Для распределенной ИТ-инфраструктуры предприятия, состоящей из нескольких серверов, для каждого из которых необходимо анализировать десятки/сотни временных рядов, использование авторегрессионных моделей доста- точно трудозатратно.

Различные модели нейронных сетей весьма распространены для прогнозирования компьютерных систем [8] и позволяют проанализировать нелинейные закономерности в наборах данных. С другой стороны, использование нейронных сетей также требует дополнительной предобработки данных, включающей нормализацию значений рядов и приведение к стационарному виду. К тому же нейронные сети работают по принципу черного ящика, что затрудняет интерпретацию модели.

Модель Хольта – Винтерса относится к классу моделей экспоненциального сглаживания. Модель успешно применяется в разных областях, в ИТ-системах находятся примеры использования для прогнозирования сетевого трафика и дальнейшего обнаружения аномалий [6; 9]. Данная модель позволяет распознавать тренд и сезонную компоненту и требует меньшей подготовки данных, чем рассмотренные выше модели. Мультипликативная модель описывается следующей системой уравнений [10]:

R _t = α SY^t + (1 – α)( R_{t – 1} + T_{t – 1});

T_t = β( R_t – R_{t – 1}) + (1 – β) T_{t – 1};

S_t = γ S y ^t +(1 – γ) S_{t – L} ;

Yt + m = (St + mTt)St – L + m, где Rt – экспоненциально-сглаженный ряд; Tt – значение тренда; St – сезонная составляющая ряда; Yt + m – функция прогноза на m шагов; α, β, γ – коэффициенты сглаживания ряда, тренда и сезонности; L – период сезонности.

Для реализации модели Хольта – Винтерса и решения системы уравнений необходимо определить период сезонности L и оптимальные значения параметров α, β, γ. Следует провести экспериментальные исследования для анализа применения данной модели. Оценка точности модели осуществляется с помощью средней абсолютной ошибки в процентах (MAPE):

I z ( t ) - Z 0)| Z ( t )

1 ^N MAPE = —У

N^

t = 1

Экспериментальные исследования

Для проведения экспериментальных исследований была произведена подготовка необходимых данных, представленных в виде временных рядов. В течение недели с дискретностью в 10 минут с двух корпоративных серверов производственного предприятия

Выпуск 4/2019

в Тюмени фиксировались значения трех параметров. Достаточность данных параметров для оценки работоспособности серверов в рамках данной статьи не рассматривается. Зафиксированы значения следующих параметров:

• 1.    CPU load (загрузка центрального процессора).

• 2.    Memory usage (использование физической памяти).

• 3.    Outgoing network traffic (исходящий сетевой трафик).

Все операции с временными рядами и их графиками производились в специализированном программном обеспечении Statistica. Рассмотрим графики временных рядов использования физической памяти (рис. 1) и загрузки центрального процессора (рис. 2) первого сервера.

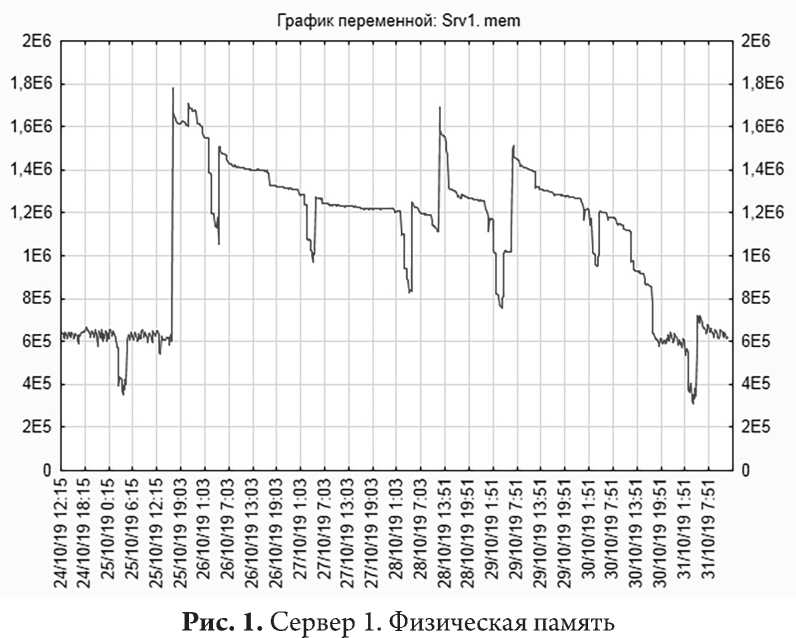
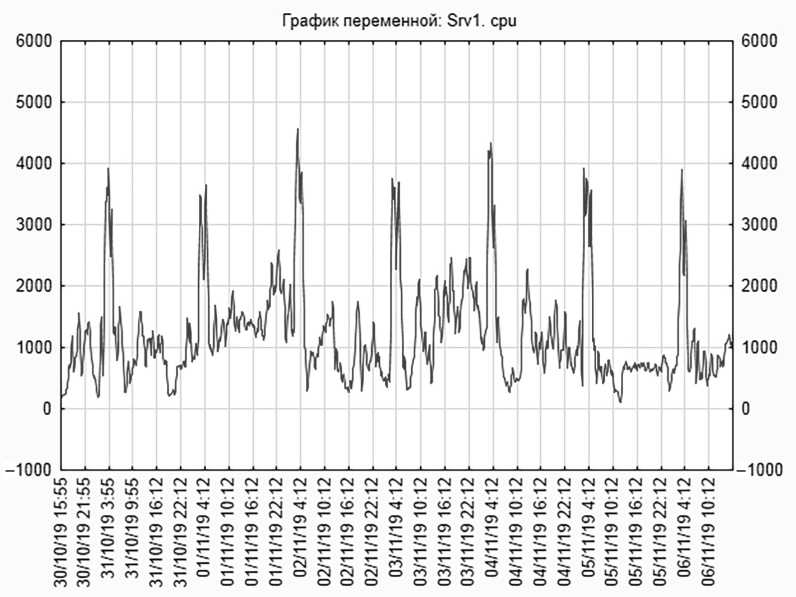
Рис. 2. Сервер 1. Загрузка процессора

Дубровин М.Г., Глухих И.Н. Применение модели Хольта – Винтерса...    39

В связи с присутствием шумов для лучшего отображения динамики рядов временные ряды предварительно сглажены скользящим средним с шагом в две единицы. Визуальный анализ показывает, что данные графики отражают присутствие тренда и мультипликативной сезонности периодом в сутки (144 измерения).

Для каждого исходного ряда построена мультипликативная модель Хольта – Винтерса с линейным трендом. Лаг сезонной компоненты L выбран в качестве 144 измерений. Выбор коэффициентов α, β, γ осуществлялся с помощью встроенного в Statistica алгоритма автоматического поиска.

Результаты экспериментов на обучающей выборке представлены в таблице. Среднее значение оценки MAPE составляет 10,2%. Считается, что модель показывает высокую точность при MAPE меньше 10% и хорошую – при MAPE от 10 до 20% [1]. Таким образом, можно сделать заключение, что модель Хольта – Винтерса демонстрирует достаточно хорошие результаты для прогнозирования параметров серверов. Для сравнения: эксперименты по анализу модели SARIMA для прогнозирования часовой загрузки двух серверов показали значения точности в 11,46 и 11,67% соответственно [7]. В ходе эксперимента также выявлено, что модель показывает менее точные результаты на рядах с повышенным уровнем шума.

Результаты экспериментов

№ п/п	Сервер	Параметр	L	α	β	γ	MAPE, %
1	1	CPU load	144	1	0	0	14,8
2	1	Memory usage	144	0,9	0	0	2,3
3	1	Outgoing network traffic	144	0,4	0,1	0	11,3
4	2	CPU load	144	0,5	0	0	13,7
5	2	Memory usage	144	0,9	0,1	0	6,4
6	2	Outgoing network traffic	144	0,3	0,1	0	12,7

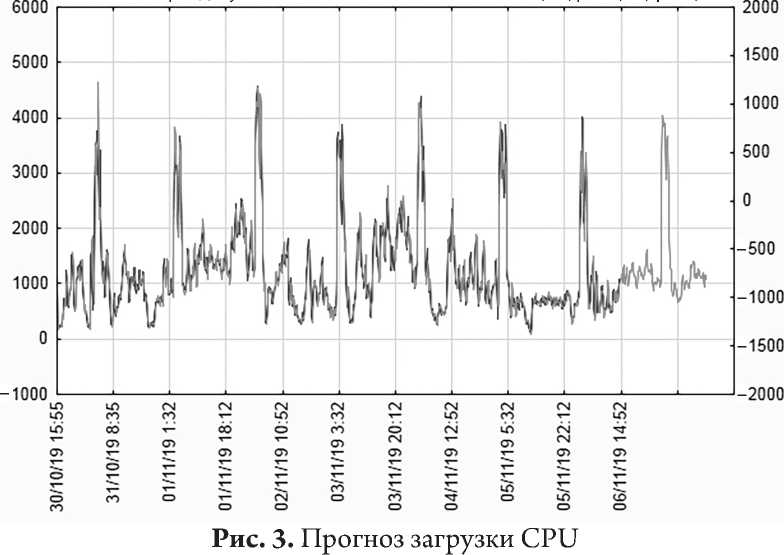
Далее продемонстрирован прогноз загрузки центрального процессора первого сервера на сутки вперед с помощью модели Хольта – Винтерса (рис. 3).

Экспоненциальное сглаживание: Srv1. cpu

Мультипликативная сезонность: (144)

Линейный тренд мультипликативной сезонности: α = 1,00, β = 0,00, γ = 0,00

40 в ыпуск 4/2019

Темной линией на графике обозначен временной ряд статистических данных. Светлой линией отображается временной ряд прогнозных значений. На графике видно, что при формировании прогнозных значений учитывается тренд-сезонная динамика ряда.

Выводы

В процессе сравнительного анализа моделей прогнозирования сделано следующее заключение. Для использования модели Хольта – Винтерса не требуется трудозатратных операций по предварительной обработке значений временных рядов, что является преимуществом при анализе распределенной ИТ-инфраструктуры предприятия, состоящей из нескольких серверов, для каждого из которых необходимо анализировать десятки/сот-ни временных рядов.

Проведены экспериментальные исследования по оценке использования модели Хольта – Винтерса для прогнозирования параметров серверных систем. Полученные значения оценки точности модели MAPE лежат в диапазоне от 2,3 до 14,8%, среднее значение MAPE составляет 10,2%. Можно сделать заключение, что модель Хольта – Винтерса показывает достаточно хорошие результаты и может быть использована для решения практических задач.