Применение модернизированной модели струйного течения для расчета движения физиологических жидкостей в живом организме

Подавляющее большинство физиологических процессов в человеческом организме требует переноса жидкостей по длинным тонким каналам широкого диапазона размеров: диаметр сечения — от нескольких мкм до мм, длина — десятки мм. При этом во многих случаях обоснованно применяется приближение пуазейлевого профиля скорости. В том случае, когда происходит переход узкого канала (например, капилляра) в более широкий (вена, артерия и т. д.), представляется допустимым использовать схемы струйного течения. При изучении движения крови в легких (т. н. малый круг кровообращения), т. е. в условиях малых давлений (15–25 мм рт. ст.), при диаметрах капилляров порядка 3–11 мкм, диаметры артерий и вен — от 4 мм до 25–30 мм. Малые давления соответствуют относительно широким струям.

Некоторые аспекты формирования струйного течения рассмотрены в нашей работе [1]. За основу была взята модель затопленной струи Л.Д. Ландау и ее развитие [2]. Альтернативным подходом, по-видимому, может явиться фокусировка потока [3]. Правда, в этом случае физические механизмы в малой степени соответствуют процессам, проходящим в организме. Задачи, связанные с гемодинамикой, и ряд родственных задач традиционно решаются с применением программного пакета COMSOL MULTIPHYSICS, например в [4, 5]. В частности, в [4] рассматривается возможность

использования не только естественных для крови моделей неньютоновской жидкости, но и приближения ньютоновской жидкости. Основная проблема заключается в том, что данные расчета в COMSOL и по модели затопленной струи имеют существенные расхождения. В то же время для ряда задач желательно иметь простое адекватное аналитическое решение.

ПОСТАНОВКА ЗАДАЧИ И РЕШЕНИЕ

Имеется потребность в простой оценочной формуле на основе струйного течения, т. к. основные особенности геометрической схемы (тонкий канал, входящий в более широкий канал или камеру) хорошо согласуются с предпосылками модели. Рассматриваются режимы движения с поперечными числами Рейнольдса порядка 0.01, продольными — не превосходящими 1.

Согласно [3], радиальная компонента вектора скорости течения

Vr =1F (0), r

F(0)=2v

'A--1

( ( A - cos( 0 )) ²

^

- 1

где θ — угол от оси струи, r — радиальное перемещение, ν — коэффициент кинематической вязкости. Для модели неньютоновской жидкости с учетом не очень большого диапазона изменения рассматриваемых скоростей можно изначально

использовать кажущуюся, или пластическую, вязкость. Параметр А — константа интегрирования, определяется через радиальную компоненту тензора потока импульса в струе П rr = p + p V r V r , где p — давление, ρ — плотность жидкости. Для полной неусеченной струи получим полный поток импульса W :

π

W = 2n j r 2 П _rr cos(0 )sin( 0 )d 0 , поскольку 0

П

rr

4V ² P f ( A ² - 1) 2   - A )

r ² ( ( A - cos( 0 ))⁴   A - cos( 0 ) _?

Данная формула основывается на первом приближении затопленной струи. В [1] была предложена модификация модели, состоящая в учете вертикального среза струи, корректировке потока импульса на неполную площадь сечения, и пересчет на энергетически эквивалентную неусеченную струю с другой константой А и, как следствие, с другим значением радиальной скорости. В нашем случае имеет место иной эффект, условно называемый влиянием задней стенки.

Наблюдается отклонение первого приближения от численного решения уравнения Навье—Стокса с помощью метода конечных элементов с применением программного пакета COMSOL (см. рис. 1). Первым вариантом модификации модели является использование второго струйного приближения. Коэффициенты зависимости формально определены по первым двум отсчетам. Таким образом, на рис. 1 наблюдается существенно лучшая сходимость оценок к результатам счета в сравнении с первым приближением.

Однако этот результат, во-первых, достигается чисто формально: аппроксимирующая функция с двумя параметрами практически всегда обеспечивает качество аппроксимации более высокое по сравнению с однопараметрической зависимостью. Во-вторых, для камеры с более далекой задней стенкой (4 мм по сравнению с 2 мм) необходимость второго приближения существенно меньшая, т. к. и первое приближение обеспечивает большую точность аналитического решения.

Таким образом, модификация должна касаться базового физического принципа — постоянства потока импульса, который при наличии близко расположенной задней стенки нарушается.

Идея состоит во внесении следующей поправки: суммирование части потока импульса, дополнительно отраженного от стенки и исходного потока. Полученное увеличение потока пересчитывается в изменение (уменьшение) константы А и увеличение скорости. Уточненное значение А находится как решение обратной задачи через (2).

Дополнительный поток вычисляется через интеграл, аналогичный (2), с пределами [0; θ ^*]. Здесь tg( θ ^* ) = r/L , где r — глубина входа струи в камеру, L — расстояние до задней стенки.

Эффект изменения скорости при учете данного фактора иллюстрирует рис. 2. Протяженность или глубина камеры (максимальная величина осевого перемещения жидкости) предполагается 2 мм, начальное значение параметра А равно 1.5.

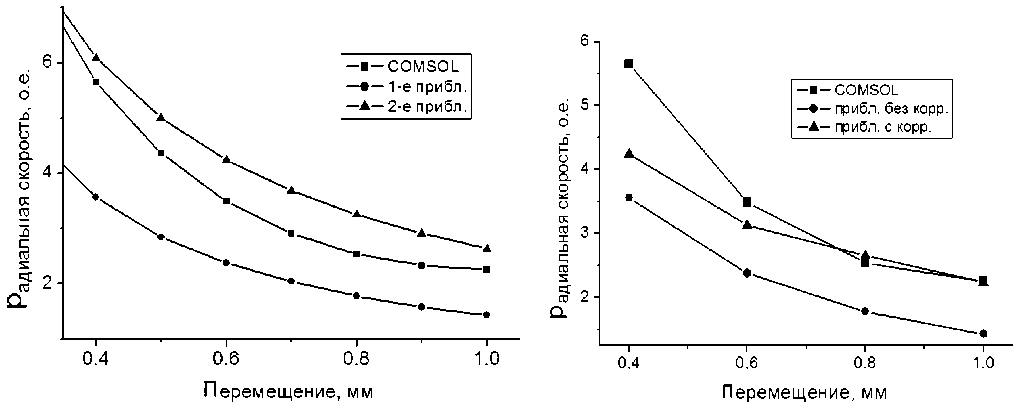
Рис. 1. Расчеты радиальной скорости ввода жидкости в камеру глубиной 2 мм, выполненные по различным методикам

Рис. 2. Иллюстрация эффекта коррекции параметров струи

Зависимость на интервале радиальных перемещений от 0 до 0.4 мм практически является формальным следствием "обучения" модели по первым 1–2 отсчетам. Таким образом, этот участок нерепрезентативен для анализа точности аппроксимации. Влияние коррекции параметра А на погрешность аппроксимации можно оценить на основе критерия Фишера значимости дисперсий двух случайных величин. В этом случае среднеквадратичная величина разности приближенного аналитического решения и численного решения с помощью COMSOL рассматривается как дисперсия соответствующей случайной величины. Для обоих вариантов приближения расчет по 12 точкам дает значения среднеквадратичной погрешности 2.28 и 0.71, а их отношение — примерно 3.21. Процентные точки распределения Фишера для двух выборок объемом по 12 измерений составят: для α = 0.05 — значение 2.82 и для α = 0.01 — значение 4.46. Таким образом, нашему случаю соответствует очень высокий уровень значимости (порядка 4 %). Это статистически подтверждает существенно более высокую точность аппроксимации при использовании модели струи с коррекцией параметра А .

ЗАКЛЮЧЕНИЕ

Из рис. 2 следует, что для области камеры, не слишком удаленной от задней стенки, т. е. при сопоставимости осевого перемещения жидкости и расстояния до задней стенки, корректировка величины Π rr (2) и далее параметра А (1) позволяют уточнить оценку величины радиальной скорости на оси струи и многократно уменьшить расхождение численной оценки и аналитического решения на основе первого струйного приближения. В случае "пульсирующего" течения вместо радиальной скорости скорее всего потребуется рассматривать усредненное по периоду пульсации значение.

Ответ на вопрос, в какой мере данный подход применим к иным геометрическим схемам переноса вещества, пульсирующего режима течения и неньютоновской жидкости, требует дальнейшего анализа и расчета. Однако идея коррекции параметров при сохранении в модернизированном варианте закона сохранения радиальной компоненты потока импульса показала состоятельность на рассмотренном примере.

При движении крови в легких диаметры капилляров — порядка 10 мкм, диаметры артерий и вен — от 4 мм до 30 мм. По сопоставлению размеров кровеносных сосудов видно, что схема ввода узкого потока в камеру практически неограниченных размеров, характерная для затопленной струи, не противоречит геометрическим параметрам сосудов кровеносной системы. Малые давления (15– 25 мм рт. ст.) соответствуют относительно широким струям с параметром А, равным 1.4 и более. Тем самым предложенный алгоритм построения приближенного аналитического оценочного решения можно считать применимым.

Работа выполнялась в рамках государственного задания по проекту "Микрофлюидные устройства и системы для имитации и исследования процессов в живом организме" (№ 0074-2016-0003).