Применение модифицированного алгоритма ранговой корреляции для анализа соответствия математической модели средств обнаружения на основе линий вытекающей волны экспериментальным сигналам
Автор: Духан Евгений Изович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Электромагнитная совместимость и безопасность оборудования
Статья в выпуске: 2 т.8, 2010 года.
Бесплатный доступ
В статье статистическими методами обосновывается адекватность математической модели, применяемой для теоретического исследования процессов сигналообразования в средствах обнаружения на основе линий вытекающей волны. Для повышения надежности принятия решения предлагается ориги- нальная модификация метода ранговой корреляции Кендала.
Физические средства обнаружения, математическая модель, метод ранговой корреляции кендала, соответствие расчета и эксперимента
Короткий адрес: https://sciup.org/140191398
IDR: 140191398 | УДК: 621.391
Текст обзорной статьи Применение модифицированного алгоритма ранговой корреляции для анализа соответствия математической модели средств обнаружения на основе линий вытекающей волны экспериментальным сигналам
Физический принцип действия средств обнаружения на основе линий вытекающей волны (СО ЛВВ) хорошо известен. Распространение высокочастотной энергии вдоль передающего излучающего кабеля (ИК) в результате дифракционных явлений на границах раздела физических сред (грунт-воздух) приводит к появлению во внешнем пространстве электромагнитного поля весьма сложной формы. Поле передающего ИК наводит ток проводимости во внешнем проводнике приемного излучающего кабеля, который играет роль распределенной приемной антенны (см. рис. 1). Напряжение, выделяемое при этом на согласованных нагрузках, – «ближнем» и «дальнем» концах приемного ИК – называется сигналом связи. При отсутствии человека – нарушителя (ЧН) в пространстве в непосредственной близости от приемной или передающей антенн, неизменных параметрах сред распространения ЭМП, моночастотном излучении и отсутствии внешних помех уровень этого напряжения будет оставаться постоянным.
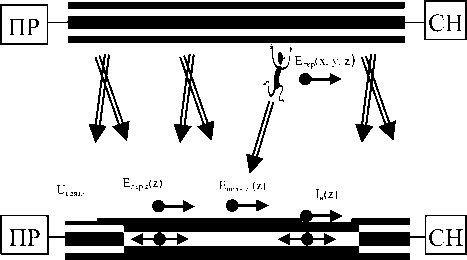
Рис. 1. Принцип действия СО ЛВВ
Переизлученное телом нарушителя поле передающего ИК вносит возмущение в распределение ЭМП вдоль приемной линии. Перемещение нарушителя вблизи места укладки ИК приводит к амплитудной и фазовой модуляции сигнала связи. Изменения амплитуды и фазы колебания на входе приемника, вызванные движением человека, являются полезной для процесса обнаружения информацией (сигналом от цели). Наряду с ним наблюдается паразитная модуляция (медленный дрейф) сигнала связи под воздействием изменения электрических параметров грунта, атмосферных явлений, колебаний растительности, внешних электромагнитных помех и др.
Моделирование процессов сигналообразова-ния в средствах обнаружения на основе линий вытекающей волны (СО ЛВВ) призвано существенно снизить затраты на проведение масштаб- ных экспериментов, без которых невозможно дальнейшее развитие обладающего уникальными тактическими характеристиками этого класса устройств. Математическая модель, изложенная в [1] позволяет осуществлять численный расчет сигнала связи и сигнала от цели в различных погодных условиях и при различных способах размещения излучающих кабелей (ИК). Модель основывается на строгом электродинамическом решении задач дифракции ЭМП вблизи плоской границы раздела сред, однако оценка ее адекватности реальным процессам, протекающим в СО ЛВВ целесообразна. Такая оценка была осуществлена с использованием теории распознавания образов.
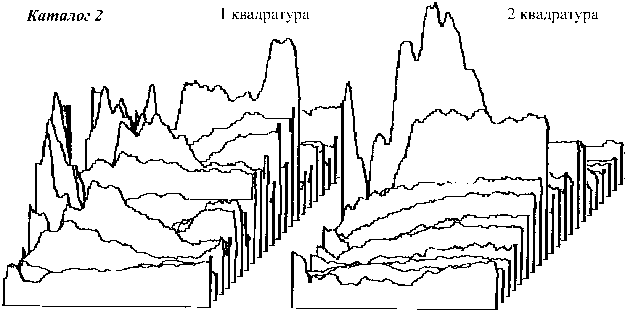
Для двух различных вариантов размещения ИК на рубеже охраны (см. рис. 2) при стабильной сухой погоде были записаны квадратурные составляющие реализаций сигналов от нарушителя, пересекающего трассу укладки ИК под прямым углом. В обоих случаях воздушный кабель (№ 4) играл роль передающей ЛВВ, подземные кабели поочередно подключались к приемному устройству. Для исключениявлияния нарезультат эксперимента эффектов отражения от концов ИК реализации снимались в срединной части трассы с шагом по продольной координате в 1 метр, нормировались по длительности (по количеству отсчетов) и объединялись в два каталога К1 (приемный кабель № 6) и К2 (приемный кабель № 5) по 22 пары квадратур в каждом. Для этих же погодных условий и параметров размещения кабелей на рубеже охраны на основе математических моделей были рассчитаны теоретические сигналы от двигающегося нарушителя – М1 и М2 . На рис. 3-4 приведены квадратурные составляющие экспериментальных реализаций из каталогов 1 и 2 и соответствующие им математические модели.
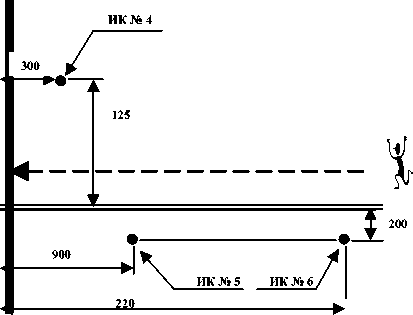
Рис. 2. Устройство экспериментальной трассы
Для определения степени схожести двух последовательностей чисел – в нашем случае модель и реализация – в теории распознавания образов вводится понятие расстояния, которое является некоторой функцией d от эталонного вектора M (модель) и испытуемого вектора К (практическая реализация). С целью вычисления расстояния широко используются различные математические выражения: Чебышевское и Евклидово расстояние, расстояние по Манхэттену и Каммберу и др. В каждом конкретном случае выбирается оптимальная функция из имеющегося немалого арсенала.
Неравномерность чувствительности исследуемого средства обнаружения по продольной координате приводит к тому, что полезный сигнал от реализации к реализации существенно отличается по амплитуде. При этом формы квадратурных составляющих полезного сигнала должны соответствовать теоретически рассчитанным моделям. В такой ситуации оптимальной мерой сходства между эталонной моделью и практическими реализациями оказалась ранговая оценка расстояния, предложенная в работах М. Кендала [2]:
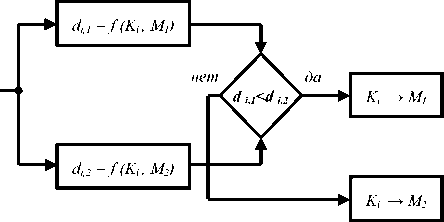
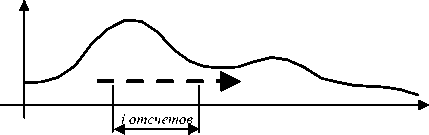
d=f(K,M) =1—— ^AM-aP, (1) n • (n-1) l + 1 при M l > M k, A M lk < - 1 при M l < M 0 при M l = M для опорной последовательности (модели) и '+ 1 ^риР1> pk, AP 4 - 1 прир1 < pk, 0 ^рир1 = pk для испытуемой последовательности (реализации). Модель 1 Рис. 3. Практические реализации и модели каталога 1 Рис. 4. Практические реализации и модели каталога 2 Как известно, число размещений из n по 2 равно n (n – 1), поэтому при одинаковой упорядоченности отсчетов в сравниваемых последовательностях расстояние между ними будет равно нулю. Максимальное (равное 2) расстояние между анализируемыми последовательностями соответствует противоположной упорядоченности отсчетов. При независимых коэффициентах сравнения, то есть при независимости опорной и оцениваемой последовательностей, расстояние d принимает единичное значение. Применение в качестве классифицирующего правила рангового алгоритма обосновывается тем, что он базируется на понятии «сходства» формы между разделяемыми сигналами. Коэффициент сравнения, вычисляемый по формуле Кендала, зависит от того, насколько однотипно упорядочены предъявляемые последовательности, и не зависит от их абсолютного значения. Свойство инвариантности применяемого алгоритма к амплитуде исследуемых сигналов позволяет избежать лишних вычислений в условиях существенной продольной неравномерности чувствительности средства обнаружения. Решающей программе предъявлялись реализации обоих каталогов экспериментальных сигналов. Программа классифицировала каждую предложенную реализацию по двум классам. В качестве разделяющих эталонов (прототипов классов) использовались теоретические реализации сигналов от нарушителя. Решающий автомат вычислял «расстояние» по Кендалу между очередной опытной реализацией и имеющимися моделями для каждой квадратурной составляющей. Алгоритм работы классифицирующей программы приведен на рис. 5. По результатам сравнения полученных расстояний испытуемая реализация относилась к одному из возможных классов. Результаты автоматической классификации квадра- турных составляющих экспериментальных сигналов приведены в таблице 1. Рис. 5. Алгоритм классификации Как видно из таблицы, первые квадратурные составляющие 18-ти из 22-х реализаций каталога К1 были отнесены к классу, эталонной последовательностью которого являлась модель М1. Лишь 4 реализации были отнесены решающей программой к классу сигналов, соответствующих модели М2, то есть классифицированы не верно. Первые квадратурные составляющие реализаций каталога К2 разделились между моделями так же в соотношении 4 к 18. Вторые квадратурные составляющие указанных каталогов разделились между моделями в соотношении 19 к 3 и 10 к 12. Таблица 1. Результаты автоматической классификации квадратурных составляющих экспериментальных сигналов классическим алгоритмом Кендала КАТАЛОГ 1 кв. – М1 1 кв. – М2 2 кв. – М1 2 кв. – М2 К1 18 4 19 3 К2 4 18 10 12 Результаты классификации, приведенные в таблице 1, уже говорят в пользу сходимости рассчитанных теоретически и снятых экспериментально результатов. Числовая степень их соответствия была оценена путем проверки гипотезы о «независимости признаков» с помощью известного критерия χ2 [3]. В данном случае первым из признаков является априорная принадлежность практических реализаций к соответствующему каталогу (К), а вторым – результат их машинной классификации (М). При этом сам результат классификации можно трактовать как таблицу сопряженности указанных признаков. В ситуации, когда признаки принимают только два значения (в данном случае – реализация принадлежит классу М1 или М2) статистика Х2, имеющая распределение χ2 с одной степенью свободы рассчитывается наиболее просто (см. таблицу 2): . n(nunM - n„n2, )2 X2 = 11-^2-----12 21 , (4) n1•n2• n•1n•2 где nij – частота событий типа «реализация из i-го каталога была отнесена к j-му классу, n·j = n1j +n2j – число проявлений признака Mj – общее число реализаций, отнесенных к j-му классу), ni·= ni +ni2 – число проявлений признака Ki – общее число реализаций в i-ом каталоге, n·– общее число испытаний. Для простоты расчета деление сигналов на квадратуры не производилось. Рассчитанное согласно этой таблице значение критерия независимости оказалось равным χ2 = 24,7, что отвергает поставленную гипотезу с высокой степенью достоверности (вероятность ошибки второго рода меньше чем 10-3). Правомерность применения самого критерия χ2 была также проверена. Несостоятельность выдвинутой гипотезы статистически доказывает неслучайность классификации распознающим алгоритмом квадратурных составляющих практических реализаций относительно опорных теоретических моделей.Из чего можно сделать вывод об адекватности ис- Таблица 2. Общий вид таблицы сопряженности для случая двузначных признаков КАТАЛОГ М1 М2 ∑ К1 n11 n12 n1• К2 n21 n22 n1• ∑ n•1 n•2 n•• Таблица 3. Таблица сопряженности признаков по результатам классификации (1) КАТАЛОГ М1 М2 ∑ К1 37 7 44 К2 14 30 44 ∑ 51 37 88 Таблица 3. Результаты автоматической классификации квадратурных составляющих экспериментальных сигналов модифицированным алгоритмом Кендала КАТАЛОГ 1 кв. – М1 1 кв. – М2 2 кв. – М1 2 кв. – М2 К1 19 3 19 3 К2 3 19 9 13 пытуемой модели реальным физическим про-цессам,имеющим место в СО ЛВВ. Резонно предположить, что в ходе машинного эксперимента неверно были классифицированы реализации, уровень полезного сигнала которых минимален,а относительное «зашумление» максимально. Однако тщательный анализ неправильно классифицированных сигналов показал,что часть реализаций,оши-бочно отнесенных к чужому классу, имеют нетипичное соотношение максимумов и минимумов. Такое положение вещей позволило выдвинуть гипотезу, что при наличии в классифицируемых последовательностях нескольких интервалов монотонности использование традиционного алгоритма Кендала, учитывающего соотношение отсчетов испытуемых последовательностей по всей их длине, не всегда эффективно. Лучшей производительностью в такой ситуации должен обладать модифицированный кендаловский алгоритм, набирающий статистику в некотором скользящем «окне», длиной i отсчетов (см. рис. 6): d = 1- i (i—1) • (n—i +1) AM AP ■ lk lk l Очевидно, что протяженность скользящего окна имеет некоторое значение, оптимальное по критерию наилучшего качества классификации. Длину окна необходимо подбирать в период «обучения» классифицирующего алгоритма. При проведении машинного эксперимента было выяснено, что оптимальная протяженность окна примерно равнялась средней по теоретическим последовательностям длине интервалов монотонности, которая соответствовала среднему интервалу их корреляции. Результаты классификации квадратурных составляющих экспериментальных сигналов из каталогов К1 и К2 относительно моделей оконным алгоритмом Кендала сведены в таблицу 4. Рост достоверности классификации экспериментальных реализаций наблюдался для трех из четырех групп квадратурных составляющих. Значение χ2, рассчитанное на основании таблицы 4, увеличилось до 31,3. Рис. 6. Расчет «расстояния» между списками в скользящем окне Для проверки правильности гипотезы о преимуществе предложенного модифицированного алгоритма Кендала были проведены аналогичные эксперименты для ряда других пар каталогов практических реализаций, протяженность которых равнялась протяженности реализаций каталогов К1 и К2. При этом считалось, что обучение распознающего алгоритма – подбор оптимальной длины окна – было осуществлено в ходе работы с первой парой каталогов.Во всех случаях при использовании скользящего окна в классическом алгоритме Кендала наблюдался небольшой выигрыш в качестве работы классифицирующей программы. На основании проведенных численных экспериментов можно сделать два важных для дальнейших исследований вывода: 1. Адекватность предложенной в [1]математи-ческой модели физических процессов, протекающих в средствах обнаружения на основе линий вытекающей волны, подтверждается статистически. 2. При классификации последовательностей, имеющих не постоянный тренд, а несколько интервалов монотонности,методами распознавания образов с использованием ранговых алгоритмов целесообразно применять модифицированный алгоритм. «Оконный» алгоритм Кендала позволяет для некоторых классов последовательностей не только увереннее распознавать испытуемые сигналы,но и существенно снизить вычислительные затраты на его реализацию.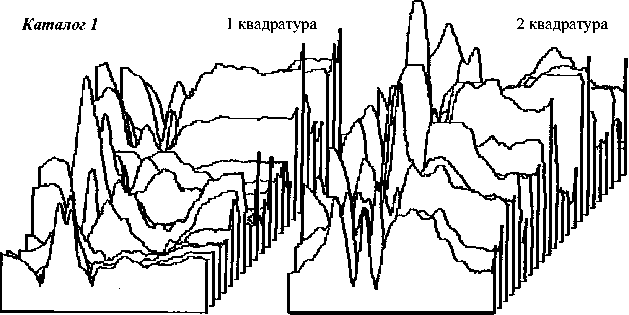
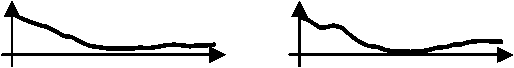
Список литературы Применение модифицированного алгоритма ранговой корреляции для анализа соответствия математической модели средств обнаружения на основе линий вытекающей волны экспериментальным сигналам
- Бакланов В.В., Духан Е.И. Моделирование процессов сигналообразования в двухкабельных средствах обнаружения на основе линий вытекающей волны//Территориальные распределенные системы охраны. №7, 2009. -С. 31-35.
- Фор А. Восприятие и распознавание образов. Пер. с франц. М.: Машиностроение, 1989. -354 с.
- Тюрин Ю.Р., Макаров А.А. Анализ данных на компьютере. М.: Финансы и статистика, 1995. -384 с.


