Применение нейронной сети для текущего анализа нестационарного сигнала (речи), представленного его вейвлет-отображением. II. Исследование и оптимизация нейронной сети

( S n + 1 ) ^T - [ V ² { E [ w ( n )]}] S n = 0.         (34)

Условие (34) — это условие ортогональности вектора направления S _{n +1} на ( n +1) шаге относительно вектора     [ V ² { E [ w ( n )]}] S _n ,     где

V ² { E [ w ( n )]} — матрица Гессе (33).

Корректировка вектора весов персептрона выполняется по соотношению

~

Н ( n ) - p ( n ) = - g ( n ).                  (30)

^w n + 1 = ^w n ⁺ ^ n ^S n .                ⁽³⁵⁾

Изменение весов персептрона A w ( n ) вдоль этого направления с параметром скорости обучения п определяется соотношением (31):

A w ( n ) = n - p ( n ). (31)

Значение параметра X , соответствующее минимуму E ( w _{n + 1} ) в направлении вектора S n , определяется выражением

Таким образом, выражение (29) преобразуется к виду (32)

[ V E ( w n )] T - S n

S n -[ V ² { E ( w n }] - S n ’

Н ( n + 1) = Н ( n ) +

где     V E ( w _n )    — вектор градиента

+ —?---------g(n) - g (n) + gT (n)-p( n )

[ V E ( w ( n n )L = [grad{ E ( w n )] _z   ^d E ⁽ w ⁽ n ))

d w i ( n )

.

Таким образом, метод параллельных касательных требует вычисления гиперплоскости, касательной к функции ошибок, на каждой итерации.

Поэтому метод связан с большими вычислительными затратами, особенно в задачах большой размерности.

В двухмерном варианте метод основан на движении по направлению, параллельному касательной к линии постоянного уровня функции ошибок. При большой размерности аргумента (вектора весов персептрона) используются касательные гиперплоскости и движение в направлении, параллельном этим гиперплоскостям. Требование вычисления касательных гиперплоскостей и определения min{E(w n)} вдоль направления, параллель-wn ного этим гиперплоскостям, является недостатком метода. При значительной размерности вектора весов (в функции ошибок персептрона) это приводит к росту вычислительных затрат и метод постепенно теряет эффективность, снижая точность и увеличивая длительность обучения.

ВЫБОР МЕТОДА ОБУЧЕНИЯ ПЕРСЕПТРОНА ДЛЯ РЕШАЕМОЙ ЗАДАЧИ

При использовании любого алгоритма обучения персептрона важна инициализация синаптических весов и порогов нейронов сети. В качестве начальных значений весов и уровней порога нейронов для создания им равноценных условий подстройки в процессе обучения целесообразно выбирать равномерно распределенные числа. Значения параметров синаптической связи для нейрона i в сети рекомендуется обычно ограничивать ин- тервалом

2.4 2.4

^, F_i  F_i

где Fi — общее количество входов i-го нейрона [20].

Обобщая представленный выше анализ, можно утверждать, что в алгоритмах обучения персептрона для задачи детектирования речевой активности может быть использован один из рассмотренных методов, хотя наиболее совершенными представляются два из них:

― обобщенный метод дельта—дельта (правило Джекобса), который включает адаптивный выбор параметра скорости обучения;

― метод Бройдена—Флетчера, который использует приближение для производных второго порядка (матрицу Гессе) и позволяет определять величину параметра скорости обучения.

Однако только на основе теоретического анализа нельзя сделать окончательный выбор метода обучения персептрона задаче распознавания речевого сигнала, поскольку невозможно учесть поведение алгоритмов в условиях многообразия характеристик сигнала и шума, величин пауз и наличия переходных сегментов. Исходя из этого, для обоснованного выбора метода обучения проведена экспериментальная проверка алгоритмов при различных видах шумов и различных отношениях сигнал/шум на достаточно представительных данных.

Экспериментальное исследование характеристик алгоритмов обучения персептрона

В целях объективной оценки преимуществ алгоритмов обучения для детектирования речевой активности проведен компьютерный эксперимент, в котором на речевой сигнал, включающий интервалы активности и микропаузы, наложены различные виды шума:

― белый шум, имеющий равномерный спектр мощности в звуковом диапазоне частот;

― окрашенный шум с постепенным спадом спектра при росте частоты (для розового шума — 6 дБ/октава), представителем которого может служить шум пылесоса или шум льющейся воды; музыкальный фон;

― узкополосный шум, состоящий из детерминированных или случайных компонент, постоянных по своему положению и амплитуде (шум вентилятора).

Эксперимент проведен с использованием нейросетевого эмулятора Essence 1.0 [21], выполненного на языке Java и позволяющего программно моделировать многослойный персептрон с любым количеством слоев, устанавливать отдельно количество и вид активационной функции нейронов для каждого слоя, выполнять все перечисленные алгоритмы обучения и использовать различные виды ошибок.

Данными служили оцифрованные записи речевого сигнала и сопутствующего шума с частотой дискретизации 22.5 кГц. На каждом сегменте записи длительностью 20 мс выполнено вейвлет-разложение в соответствии с персептуальной моделью, вычислена средняя мощность вейвлет-коэффициентов в каждой области разложения и полученные векторы мощности вейвлет-коэффициентов нормированы.

На основе анализируемого зашумленного речевого сигнала получено 2000 векторов, которые составили два множества (обучающее и тестовое) по 1000 векторов. Использован принцип обучения с учителем, при котором сети сообщается желаемый отклик на каждый входной обучающий вектор. Программа представляет динамику изменения ошибки в процессе обучения и на тестирующей выборке. При сходимости обучения ошибка почти не изменяется, но если она недостаточно мала, то сеть усложняется и повторяется ее обучение и тестирование. Напротив, если ошибка по обучающей выборке стремится к нулю, а при тестировании сохраняет недопустимо большое значение, то размер сети уменьшается.

После ряда экспериментов с изменением размера сети для исследования различных алгоритмов обучения принята двухслойная сеть с числом нейронов десять и один (10-1) и c логистической активационной функцией нейронов. Для всех алгоритмов при равном времени обучения (2 мин) зафиксировано число циклов обучения и процент ошибочных решений по обучающей и тестовой выборкам. Эксперимент проведен для всех видов шума при отношениях среднеквадратического отклонения шума к сигналу ζ = 0.02, 0.1 и 0.3.

Результаты компьютерного эксперимента, позволяющие сопоставить различные алгоритмы обучения персептрона, содержит табл. 1, где приведено число циклов обучения и процент ошибочных решений при обучении и тестировании для нескольких уровней сложности нейронной сети, типов и уровней сопутствующего шума. Число циклов различается в зависимости от алгоритма и определяется его вычислительной сложностью. Для всех методов обучения процент ошибочных решений на обучающей выборке меньше, чем на тестовой выборке. Однако это отличие не превышает 20 %, что подтверждает адекватность выбранной модели персептрона.

При сопоставлении алгоритмов по оценке вероятности ошибочных решений наилучшие характеристики получены для метода Бройдена—Флет-чера. Вероятность ошибочных решений зависит от интенсивности шума: для ζ = 0.02 вероятность ошибочных решений по тестовой выборке не превышает 3.7 %, для ζ = 0.1 — 4.3 %, а для ζ = 0.3 — 5.5 %. Вероятность ошибочных решений для узкополосного шума и музыкального фона выше, поскольку спектральный состав шума меньше отличается от речевого сигнала.

Различаются ошибочные решения первого и второго рода [22, 23]. Пусть ω 1 — событие, состоящее в том, что текущий сегмент или фрейм содержит речевой сигнал; ω 2 — событие, состоящее в том, что текущий фрейм содержит шум; Ω 1 — решение о том, что текущий фрейм содержит речевой сигнал; Ω 2 — решение о том, что текущий фрейм содержит шум. Тогда вероятность ошибочного обнаружения речевого сигнала во время паузы определяется соотношением

P ( Ω 1 / ω 2 ) = ^{P ( Ω 1, ω 2)} .           (37)

• ^{1    2}       P ( ω 2 )

Вероятность ошибочного обнаружения паузы при наличии речевого сигнала — соотношением:

P ( Ω 2 / ω 1 ) = ^{P ( Ω 2, ω 1)} .           (38)

• ^{2    1}       P ( ω ₁ )

Компьютерный эксперимент показал, что вероятность ошибочного обнаружения паузы при наличии речевого сигнала ниже, чем вероятность ошибочного обнаружения речевого сигнала.

Табл. 1. Сравнение методов обучения персептрона

Вид шума	Относительный вклад шума	Метод обучения	Обучение			Тестирование
			Число циклов	Время, мин	Ошибка, %	Ошибка, %
1	2	3	4	5	6	7
Белый шум	0.02	Случайный поиск	500	5	10	13
		Сопряжен. градиенты	800	3.2	3.5	5.7
		Partan	600	3.3	4	4.7
		Дельта—дельта	600	3.3	4.5	5.2
		Обобщ. дельта—дельта	650	4	2.5	3.8
		Бройдена—Флетчера	700	2	2.7	3.1
	0.1	Случайный поиск	500	6.5	12	15
		Сопряжен. градиенты	900	4.5	5	8
		Partan	700	4	6.5	6.9
		Дельта—дельта	700	4	6.5	7
		Обобщ. дельта—дельта	800	4.4	5	5.3
		Бройдена—Флетчера	800	2.2	3.4	3.6

Табл. 1 ( продолжение )

1	2	3	4	5	6	7
Белый шум	0.3	Случайный поиск	900	7	14	15
		Сопряжен. градиенты	900	5	7	8.2
		Partan	1000	4.8	9.5	9.3
		Дельта—дельта	700	4	9	5.5
		Обобщ. дельта—дельта	900	45	7	7.3
		Бройдена—Флетчера	1000	2.5	4.5	4.7
Окрашенный	0.02	Случайный поиск	600	5	11	12
шум		Сопряжен. градиенты	800	3.3	3.7	6.0
		Partan	600	3.5	4.1	4.9
		Дельта—дельта	600	3.5	4.6	5.5
		Обобщ. дельта—дельта	700	4.5	2.4	4
		Бройдена—Флетчера	800	2.1	2.6	3.3
	0.1	Случайный поиск	500	6.4	12.5	13
		Сопряжен. градиенты	850	4.6	4.8	4.8
		Partan	800	4.3	6	6.8
		Дельта—дельта	600	4.1	7	7
		Обобщ. дельта—дельта	850	4	4.2	4.2
		Бройдена—Флетчера	900	2.0	3.2	3.4
	0.3	Случайный поиск	600	5	14.5	15
		Сопряжен. градиенты	800	4	6.5	6.8
		Partan	650	3.5	8	8.5
		Дельта—дельта	700	3.0	7	8.3
		Обобщ. дельта—дельта	900	3.6	6.5	6
		Бройдена—Флетчера	800	2	4.8	5
Музыкальный	0.02	Случайный поиск	500	4	10	10.5
фон		Сопряжен. градиенты	750	3.1	3.8	4.0
		Partan	650	3.5	4	4.2
		Дельта—дельта	600	3.3	4.5	4.6
		Обобщ. дельта—дельта	750	4.0	2.6	2.8
		Бройдена—Флетчера	900	2.8	2.9	3.0
	0.1	Случайный поиск	400	7	12	12.5
		Сопряжен. градиенты	800	5	5	5.2
		Partan	850	4	5.8	6
		Дельта—дельта	550	4.2	7	7.1
		Обобщ. дельта—дельта	800	3.9	4.1	4.2
		Бройдена—Флетчера	1000	2.3	3.1	3.3
	0.3	Случайный поиск	600	4.5	14	15.2
		Сопряжен. градиенты	700	4	6.7	6.9
		Partan	600	3.2	8	8.2
		Дельта—дельта	650	3.2	7.3	8
		Обобщ. дельта—дельта	800	3.5	5.3	5.6
		Бройдена—Флетчера	900	1.8	6	5.5
Узкополосный	0.02	Случайный поиск	500	5	10.5	10
шум		Сопряжен. градиенты	700	3.2	4.5	4.7
		Partan	600	3.3	5	5.4
		Дельта—дельта	600	3.6	5.8	6.2
		Обобщ. дельта—дельта	600	4	2.6	2.8
		Бройдена—Флетчера	600	2.6	3.5	3.7

Табл. 1 ( продолжение )

1	2	3	4	5	6	7
Узкополосный	0.1	Случайный поиск	600	4.5	12	11.8
шум		Сопряжен. градиенты	700	3.8	6.0	6.4
		Partan	550	3.5	6	6.6
		Дельта—дельта	700	3.8	7.0	7.3
		Обобщ. дельта—дельта	800	4.2	3.5	3.8
		Бройдена—Флетчера	800	4.5	4.1	4.3
	0.3	Случайный поиск	750	4	14	15
		Сопряжен. градиенты	900	5	8	9
		Partan	800	4.3	8.2	8.1
		Дельта—дельта	900	4.5	9	9.5
		Обобщ. дельта—дельта	1000	5	4.9	5.3
		Бройдена—Флетчера	1000	2.8	3.2	3.6

ВЫБОР СТРУКТУРЫ ПЕРСЕПТРОНА

Выбор структуры многослойного персептрона (МСП) важен, поскольку повышенная сложность сети приводит к увеличению объема вычислений и длительности обучения, возникновению неустойчивости и переобученности, которая ухудшает показатели точности на материале тестирования. Чрезмерное упрощение в свою очередь не позволяет получить хорошее качество детектирования свойств сигнала. Поэтому построение нейронной сети для системы детектирования состояния процесса связано с выбором минимальной конфигурации, обеспечивающей хорошее функционирование.

Для сети минимального размера маловероятно обучиться несущественным деталям в обучающих данных, поэтому она может давать лучшие результаты на материале тестирования. Способ реализации такого подхода — это выбор сети малой сложности и наращивание ее до получения приемлемых показателей алгоритма обучения и правильности работы на тестовом материале.

Другой подход состоит в начальном выборе сети достаточно сложной структуры, обеспечивающей приемлемую ошибку обучения, после чего производится упрощение структуры сети путем удаления избыточных нейронов. Дополнительным ресурсом является метод регуляризации структуры персептрона, в котором вместо простого критерия среднеквадратической ошибки функция риска учитывает также меру сложности структуры персептрона.

Выбор структуры нейронной сети осуществлен на основе совместного использования методов упрощения и наращивания и метода регуляризации.

Для метода наращивания в ходе проведения серии циклов обучения, основываясь на критерии ошибки (9), определялось место размещения в сети дополнительного нейрона. Одновременно из сети удалялся нейрон, веса которого флуктуировали после сходимости обучения, т. к. этот нейрон не является существенным для задачи обучения. Результаты моделирования получены на ЭВМ с использованием программы Essence 1.0 для речевого сигнала с белым шумом при отношении среднеквадратического отклонения шума и сигнала 0.1 и 0.3. Метод наращивания сложности МСП проанализирован для структур: 3-1; 5-1; 5-1-1; 5-21; 5-3-1 и двух лучших алгоритмов обучения: Бройдена—Флетчера и обобщенного правила дельта—дельта (табл. 2). Введение третьего нейрона во втором скрытом слое МСП несущественно меняет ошибку, но обнаруживает флуктуации вектора весов дополнительного нейрона в конце цикла обучения. Поэтому метод указывает на предпочтительность структуры 5-2-1.

Метод упрощения, где после каждого цикла обучения удалялся нейрон, отсутствие которого дает минимальное увеличение ошибки обучения, применен к структурам персептрона 10-3-1; 10-21; 8-2-1; 5-2-1 (табл. 3). Результаты анализа согласуются с выводом, полученным по методу наращивания.

Метод регуляризации [5] вместо критерия среднеквадратической ошибки использует функцию риска R ( w ):

R ( w ) = E ( w ) + X • E c ( w ), (39)

где E ( w ) — среднеквадратическая ошибка,

E_c ( w ) — мера сложности структуры персептрона, а параметр λ определяет относительную значимость компоненты Е_с ( w ) и служит параметром регуляризации (поскольку форма критерия R ( w ) опирается на теорию регуляризации А.Н. Тихонова). В качестве меры сложности структуры персептрона использован квадрат нормы вектора синаптических весов МСП

Ec (w) =11 w II2 = ^ wf, (40) ieC где С — множество индексов всех весов сети. Эксперимент проведен на структурах МСП 5-2-1 и 5-3-1 с изменением параметра регуляризации от 0 (в исходном состоянии сети) до 0.01 с шагом 0.001 и показал, что один из нейронов второго скрытого слоя в 5-3-1 имеет 1.5 %-й вклад в Ec (w) и может считаться несущественным. Это подтверждает результат, полученный методом наращивания сложности персептрона.

Табл. 2. Результаты определения оптимальной структуры многослойного персептрона методом наращивания

Структура МСП	Отношение шум/сигнал	Доля ошибочных решений персептрона (%)
		Обобщенное правило дельта—дельта	Алгоритм Бройдена—Флетчера
3-1	0.1	8.1	6.5
	0.3	9.7	7.0
5-1	0.1	6.5	5.0
	0.3	8.3	5.5
5-1-1	0.1	4.9	4.0
	0.3	6.9	4.5
5-2-1	0.1	3.7	3.2
	0.3	5.5	4.0
5-3-1	0.1	3.9	3.4
	0.3	5.8	4.2

Табл. 3. Результаты определения оптимальной структуры многослойного персептрона методом упрощения

Структура персептрона	Отношение шум/сигнал	Доля ошибочных решений персептрона (%)
		Обобщенное правило дельта—дельта	Алгоритм Бройдена—Флетчера
10-3-1	0.1	2.1	2.3
	0.3	4.2	3.1
10-2-1	0.1	2.3	2.5
	0.3	4.5	3.6
8-2-1	0.1	2.9	2.8
	0.3	5.0	3.8
5-2-1	0.1	3.7	3.2
	0.3	5.5	4.0

ИСПОЛЬЗОВАНИЕ ГЛАВНЫХ КОМПОНЕНТ СИГНАЛА ДЛЯ ОБУЧЕНИЯ И РАСПОЗНАВАНИЯ

Дальнейшее улучшение алгоритма детектирования речевой активности достигнуто уменьшением размерности входного вектора персептрона, которое позволило уменьшить число синаптических весов, уменьшить объем обучающей выборки и ускорить процесс обучения. Уменьшение размерности входных векторов при условии сохранения содержащейся в них информации о речевом сигнале основано на методе главных компонент [24, 25].

Входной вектор МСП x j = [ x 1 j , x 2 j ,..., x pj ] имеет p = 22 компоненты, число которых соответствует персептуальной модели. Идея метода состоит в получении p линейных комбинаций из компонент вектора — главных компонент, каждая из которых линейно независима от других. Главная компонента y выражается соотношением:

Главные компоненты, начиная с первой y1 , определяются по критерию максимальной дисперсии aT S a при условии, что вектор коэффициентов a нормирован, т.е. aTa = 1. Решение условной максимизации использует функцию ф = aTS a - X—(aTa -1) (X— — множитель Лагран-dф     —   — — жа), градиент которой ^-— = 2S a - 2X a после приравнивания к нулю дает уравнение (s - X—I)a = 0 для определения компонент вектора a. Это матричное уравнение имеет решение, если равен нулю определитель |S - X—l| = 0. Определитель представляет собой алгебраическое уравнение степени р относительно X и позволяет найти p корней, являющихся характеристическими чис-

^—      ^—

.—

y = x a ,                         (41)

где x„    x21 ... xp,

X = ^{x ,}2 ^{x 22}    ... x p ² ,

...         ...       ...       ...

_x1 N x2N ••• xpN _ a = [в,,в2,...,вp]T — вектор неизвестных коэффициентов, Х — матрица обучающих векторов размерности N × p, N — объем обучающей выборки.

Выборочная дисперсия y определяется выражением:

■'                     —'

var( y ) = a T S a ,                   (42)

где S — выборочная ковариационная матрица обучающих векторов X

S = x

x

N - 1

N

X x 2

i = 1

N

X x2/x 1/ i =1

N

X ^x 1 ^x 2

= 1

N

X x 2²

= 1

N

X ^x 1 ^x

= 1

N

X ^x 2 ^x

= 1

p

p

.

...

N

X x p/ x 1 /

= 1

...

N

X x p x 2

= 1

...

N

X xi

= 1

лами X 1 >  X ₂ > ... >  X _p ковариационной матрицы S . Наибольшее X 1 максимизирует дисперсию y 1 , а решение системы ( s - X — I ) a = 0 дает вектор a 1 , определяющий первую главную компоненту. Следующие по величине характеристические числа в качестве решения системы ( s - X I ) a = 0 дают векторы a , которые определяют остальные главные компоненты по соотношению (41). Таким образом, для р -мерных данных первая главная компонента у 1 = X • a 1 представляет собой линейную комбинацию p компонент с коэффициентами, равными нормированному собственному вектору корреляционной матрицы S , соответствующему максимальному характеристическому числу этой матрицы. Аналогично остальные главные компоненты соответствуют следующим по величине характеристическим числам матрицы S . Главные компоненты линейно независимы, и дисперсия каждой компоненты равна соответствующему характеристическому числу матрицы S.

Общая дисперсия p компонент равна следу выборочной ковариационной матрицы tr( S ) = = var( y 1 ) + var( y ₂) + ... + var( y _p ). Относительная значимость j -й главной компоненты определяется соотношением

—— var(yj) = Xj = Xj px         ~ tr( S) ”

X var(yj)

j =1

Для уменьшения размерности выполнен анализ и выбраны q наиболее значимых компонент q <  p , которые определяют η % от общей дисперсии всех p компонент. Для η = 95 … 98 % вклад оставших-

ся p – q компонент может считаться несущественным.

При проведении исследования программа Essence 1.0 дополнена методом главных компонент. Исходными данными служили 100 векторов, представляющих нормированную мощность коэффициентов вейвлет-разложения речевого сигнала в соответствии с персептуальной моделью.

Отношение сигнал/шум варьировалось от 3 до 50. Для каждого из четырех уровней шума речевой сигнал, преобразованный вейвлет-пакетом и имеющий первоначально 22 компоненты, обработан программой главных компонент, в результате чего получены 9 компонент, содержащих не менее 97.5 % энергии исследуемого сигнала. При этом допустимый уровень потери энергии составил не более η = 2.5 %. Использование главных компонент в структуре персептрона показано на рисунке. Обучение персептрона проведено с использо- ванием алгоритмов Бройдена—Флетчера и обобщенного правила дельта—дельта, т. к. они дали лучшие результаты обучения на исходных обучающих векторах. При уменьшении отношения сигнал/шум (в исследованном диапазоне 3–50) ошибка обучения возрастает на 60 % для метода Бройдена—Флетчера и вдвое — для обобщенного правила дельта—дельта Джекобса. Для белого и окрашенного шумов метод обобщенного правила дельта—дельта имеет чуть меньшую ошибку обучения (на 0.1 %) при малом отношении шум/сигнал (до 0.05) и уступает при больших уровнях шума.

Для условий узкополосного шума и музыкального фона метод обобщенного правила дельта— дельта дает меньшую ошибку обучения и тестирования на всем диапазоне уровней шума от 0.5 до 0.2 %.

•

x ₂₂

x ₁

x ₂

x ₃

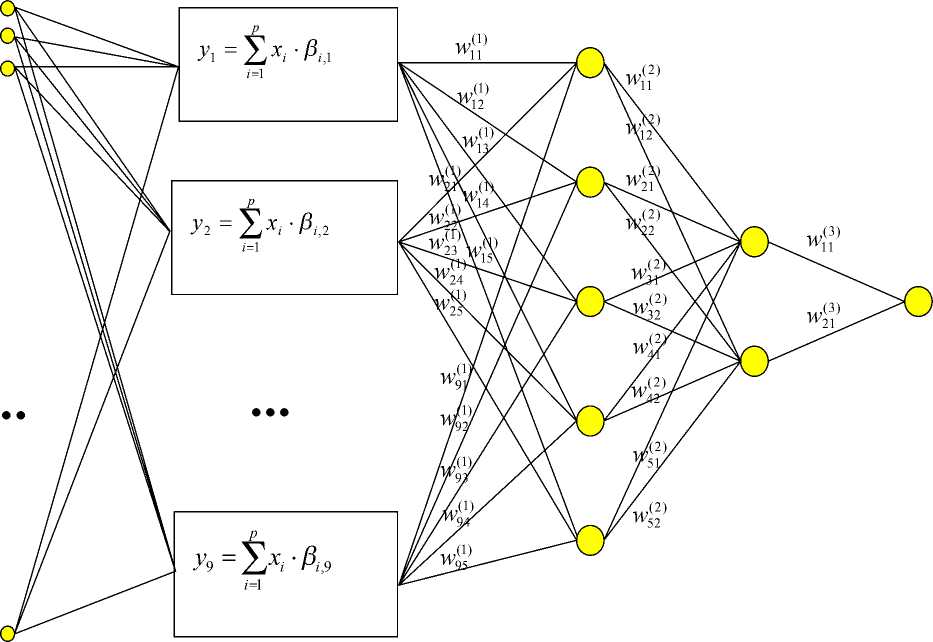
Использование главных компонент в структуре персептрона 5-2-1

Для проверки этой закономерности проанализированы алгоритмы обучения по методу сопряженных градиентов и методу параллельных касательных (метод partan), которые в аналогичных условиях давали в среднем на 1 % большую ошибку обучения, чем первые два метода. Для белого и окрашенного шумов метод параллельных касательных уступает методу сопряженных градиентов — ошибка на 1 % больше во всем диапазоне отношений шум/речь. Для музыкального фона это различие несколько меньше, а для узкополосного шума метод параллельных касательных дает уже на 0.5 % меньшую ошибку обучения.

Методы Бройдена—Флетчера и обобщенное правило дельта—дельта дают близкие показатели относительной ошибки и количество циклов обучения.

Метод главных компонент дает возможность снизить количество циклов на 30–35 % (в зависимости от метода и вида шума) и уменьшить время обучения на 40–50 %. В то же время ошибка обучения увеличивается на 0.4–0.6 %. Для узкополосного шума и музыкального фона это снижение меньше, чем для белого и окрашенного шумов, во всем диапазоне уровней шума.

Применение метода главных компонент позволило

― уменьшить размерность входного вектора персептрона с 22 до 9 компонент;

― уменьшить число оцениваемых в процессе обучения свободных параметров сети (синаптических весов) со ста двадцати двух до пятидесяти двух для нейронной сети 5-2-1;

― соответственно увеличить скорость обучения и уменьшить объем обучающей выборки.

ЗАКЛЮЧЕНИЕ

Для детектирования речевой активности предложен метод, включающий вейвлет-преобразование сигнала в соответствии с персептуальной моделью и нейросетевой алгоритм (см. статью I этой серии). Аппроксимация персептуальной модели реализована на основе вейвлет-пакета, разделяющего частотный диапазон сигнала на 22 субполосы.

Принятие решения о наличии речевой активности на анализируемом сегменте осуществлено на основе нейронной сети в форме многослойного персептрона (МСП). На входы МСП поступает нормированный вектор с компонентами, равными мощности вейвлет-коэффициентов в субполосах разложения сигнала. Исследование показало, что для обучения МСП целесообразно использовать метод Бройдена—Флетчера, который по результа- там компьютерного эксперимента имеет наилучшие характеристики по скорости обучения, величине ошибок (на обучающей и тестовой выборке) и по вероятности ошибочной классификации сегмента сигнала.

Проведены экспериментальные исследования по регуляризации структуры персептрона, основанные на методах наращивания, упрощения и регуляризации, которые показали, что оптимальной для решения данной задачи является структура персептрона 5-2-1.

Применение метода главных компонент позволяет уменьшить размерность входного вектора нейронной сети, уменьшить число оцениваемых в процессе обучения синаптических весов и увеличить скорость обучения при уменьшенном объеме обучающей выборки.