Применение нейросетевого подхода и метода на основе теории случайных функций для классификации объектов по их акустическим излучениям

В современных защитных комплексах внедряются инновационные подходы распознавания цели для эффективного поражения. Поэтому классификация сигналов является важной задачей для обеспечения безопасности стратегически важных объектов: заводы, АЭС, войсковые части и т.д.

Существуют различные способы решения задач классификации сигналов – классический, Байесовский. В последнее время становятся популярными методы машинного обучения из-за их точности.

В данной работе решалась задача классификации самолета и вертолета по их акустическим излучениям. Были применены два метода: нейросетевой подход и метод на основе теории

случайных функций. Приведены результаты обучения НС.

В качестве входных информативных признаков использовались отсчеты оценок СПМ.

ВЫБОР ИНФОРМАТИВНЫХ ПРИЗНАКОВ

Выбор информативных признаков и сокращение размерности векторов признаков являются важными аспектами при реализации систем распознавания.

Информативные признаки выбираются так, чтобы они являлись наиболее эффективными с точки зрения разделимости классов. С теоретической точки зрения наилучшим критерием эффективности информативных признаков является вероятность ошибки, а с практической точки зрения - вероятность ошибки, полученная экспериментально. Однако для данного критерия не существует явного математического выражения. В классической теории распознавания образов разделимость классов зависит не только от распределений объектов в классах, но и от используемого классификатора. В этом случае раз- делимость классов будет эквивалентно вероятности ошибки классификатора.

Важно не забывать про размерность входного вектора признаков. Слишком малая размерность может ухудшить распознавание из-за потери информации. Слишком большая размерность также отрицательно влияет на качество распознавания.

В [1-2] рассмотрены вопросы выбора информативных признаков акустических сигналов вертолета и самолета с регрессионными и нейросетевыми трактами обработки сигналов на базе реализаций, полученных в натурных условиях. Для решения выбранной задачи в качестве информативного признака использовались отсчеты оценки СПМ. Понятие «оценки СПМ» возникает, так как сигнал представляет собой случайный процесс, параметры которого точно узнать нельзя, только его оценки. Спектральная плотность мощности – функция, описывающая распределение мощности сигнала в зависимости от частоты, то есть мощность, приходящаяся на единичный интервал частоты. Она имеет размерность мощности, деленной на частоту. Выражение для СПМ имеет вид

_ l/ytcjJP

5(w) = Um — , (1) r-t= T где FT Gw) – преобразование Фурье, T – период сигнала. Спектральная плотность мощности сигнала сохраняет информацию только об амплитудах спектральных составляющих, а информация о фазе теряется. Поэтому все сигналы с одинаковым спектром амплитуд и различными спектрами фаз имеют одинаковые спектральные плотности мощности.

ПОЛУЧЕНИЕ ОТСЧЕТОВ ОЦЕНКИ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ В КАЧЕСТВЕ ВХОДНЫХ ПРИЗНАКОВ

Информативные признаки были получены из 80 реализаций самолета и вертолета, доступных в сети Интернет. На рис. 1-2 приведены реализации акустических сигналов самолета и вертолета на интервале наблюдения 1 с.

С помощью быстрого преобразования Фурье и взятие от него модуля был получен спектр сигналов для определения максимальной информативной частоты, который приведен на рис. 3-4.

Проведена фильтрация фильтром Чебышева 2-го порядка с частотой среза 10 кГц. Сглаженная оценка спектральной плотности мощности, построенная по имеющимся в распоряжении исходным последовательностям отсчетов 80 реализаций сигналов самолета и вертолета иллюстрируется рис. 5-6.

Данный информативный признак имеет недостаток – он не инвариантен к скорости полета вертолета, так как частота вращения винта может изменяться в некотором диапазоне в процессе полета в зависимости от режима. Поэтому в системе распознавания необходим блок адаптации.

Как видно из графиков, для вертолета характерна гребенчатая структура СПМ. Данный признак демонстрирует различие между двумя классами, что, в свою очередь, должно повлиять на работу классификатора. Положение максимумов по оси частот кратно основной гармонике акустического шума вертолета j^^, а положение минимумов соответствует частотам T + ^ПЛ1) n = 0, 1, 2… [4].

t, c

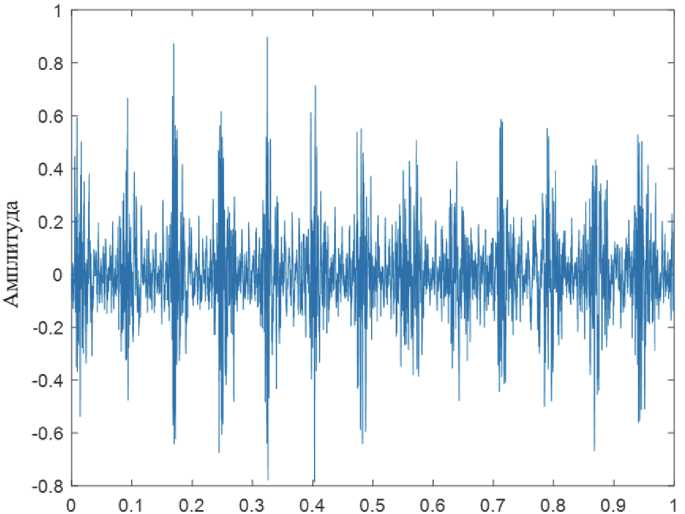
Рис. 1. Реализация сигнала вертолета

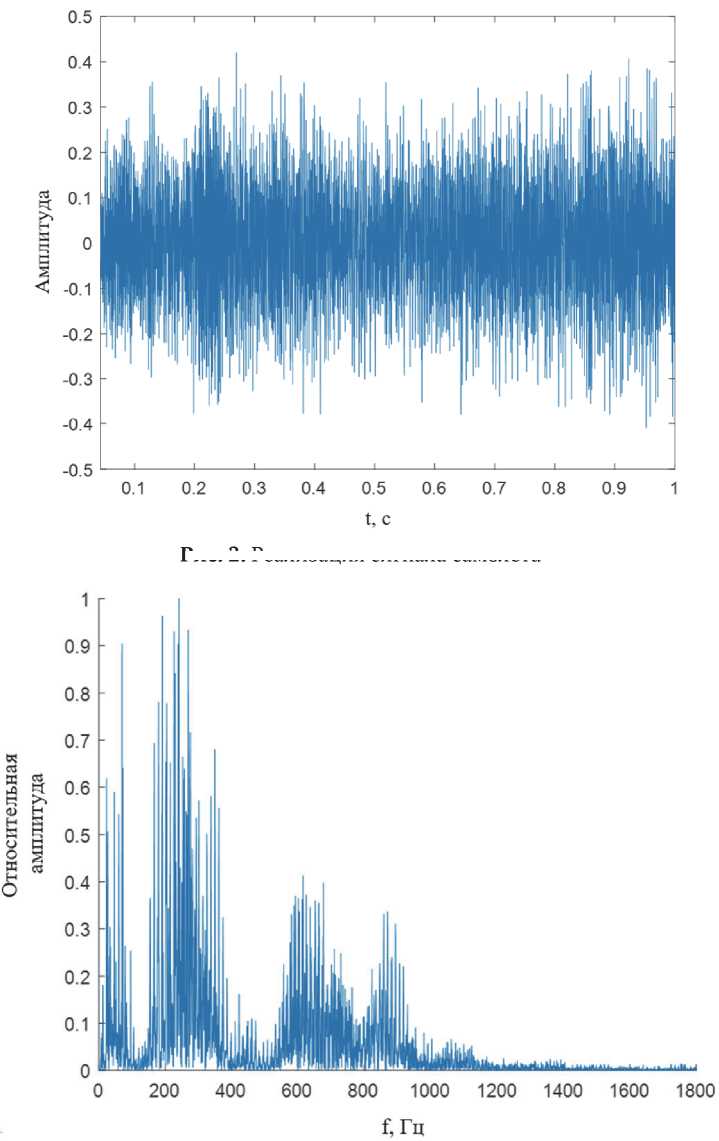
Рис. 2. Реализация сигнала самолета

Рис. 3. Спектр сигнала вертолета

НЕЙРОСЕТЕВОЙ МЕТОД КЛАССИФИКАЦИИ СИГНАЛА

Для решения задачи использовалась встроенная функция среды MATLAB, которая реализует не глубокую нейронную сеть прямого распространения. Исходя из результатов полученных в [1], для исследования выбрана НС с количеством слоев равным 3. В [4] показано, что трехслойная НС с последовательными связями способна реализовать произвольную область принятия решения.

Обучение НС производилось при помощи метода сопряженных градиентов. Данный метод более эффективен по сравнению с классическим алгоритмом наискорейшего спуска, и метода множественной линейной регрессии для неслучайной инициализации весовых коэффициентов, так как позволяет обучить сеть быстрее [8].

При обучении НС предполагалось, что учитель точно знает тип объекта для каждой реализации. Обучение нейронной сети проводилось на множестве из 60 реализаций, по 30 реализа-

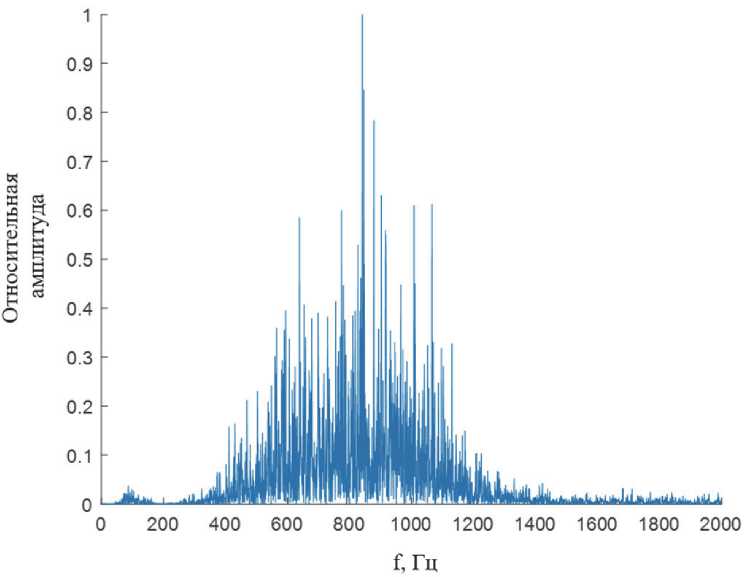
Рис. 4. Спектр сигнала самолета

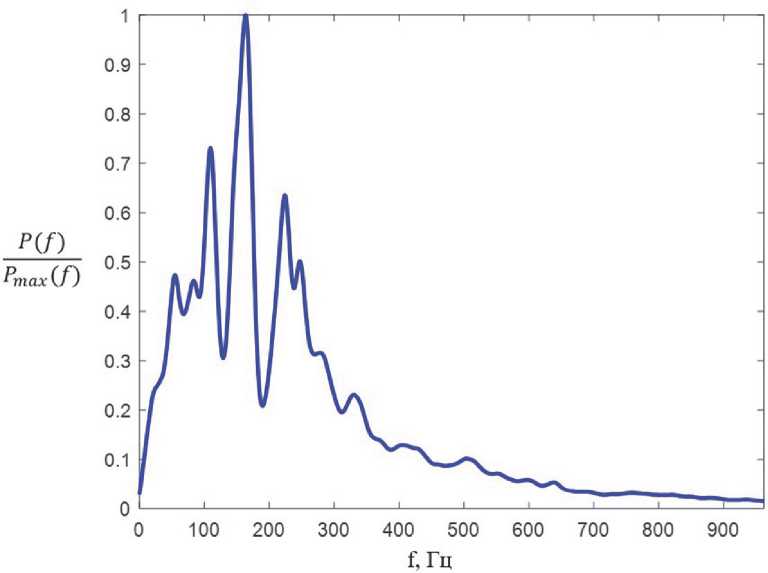
Рис. 5. Сглаженная оценка спектральной плотности мощности реализации сигнала вертолета

ций для каждого класса. Тестирование НС проводилось на множестве из 20 реализаций, по 10 реализаций для каждого класса.

Одним из фактров, влияющих на результат работы НС, является число нейронов в скрытом слое. Поэтому была исследована ошибка классификации нейронной сети при различных обучающих и тестовых выборках и числа нейронов в скрытом слое. Ошибку классификации НС на тестовой и обучающей выборке иллюстрирует рис. 7.

Как видно из графика, ошибка классификации при увеличении числа нейронов не стремится к конечному значению. Известно, что большое количество нейронов негативно влияет на время обучения и быстродействие сети. Исходя из этого, было выбрано колличество нейронов в скрытом слое равное 10.

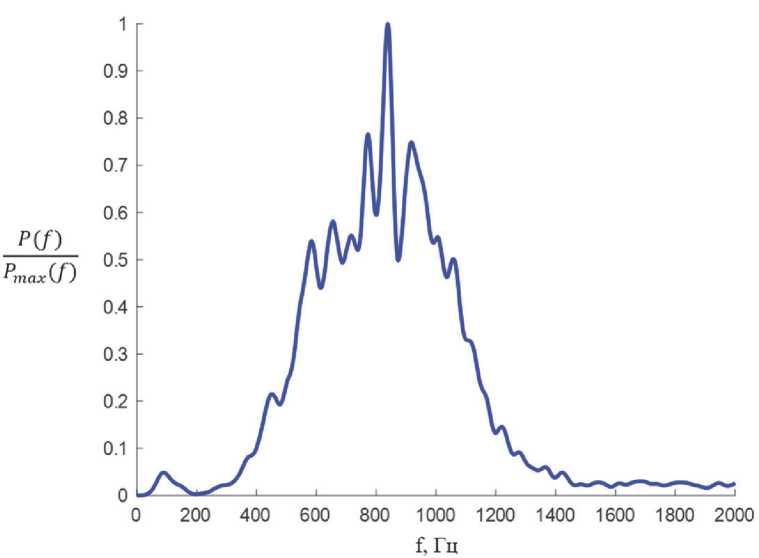
Рис. 6. Сглаженная оценка спектральной плотности мощности реализации сигнала самолета

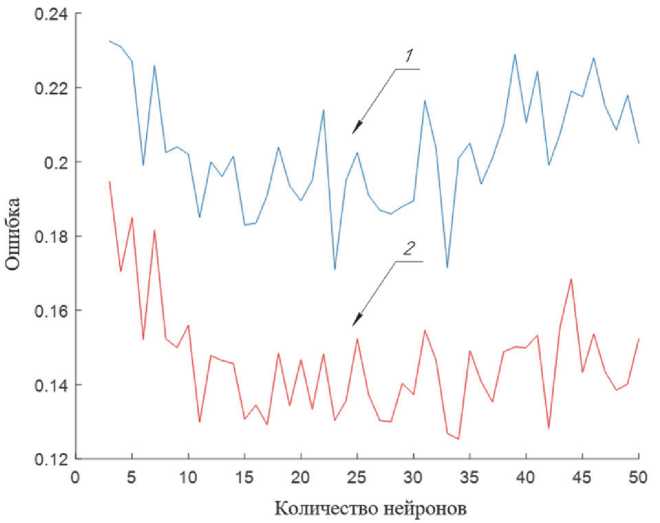
Рис. 7. Ошибка классификации НС на тестовой и обучающей выборке: 1 – тестовая выборка; 2 – обучающая выборка

В результате была получена НС с числом нейронов в скрытом слое равным 10. Число нейронов во входном слое сведено к 50. Число нейронов в выходном слое равно 1. Выходной нейрон выдает результат «1», если сигнал – вертолет и «0», если сигнал – самолет. Структуру НС иллюстрирует рис. 8.

Проводилось экспериментальные исследования на 80 имеющихся реализациях и вычисление ошибки классификации. Результат рабо- ты приведен на рис. 9. Ошибка классификации объектов (вертолет, самолет) на тестовой выборке представлена в табл. 1.

МЕТОД КЛАССИФИКАЦИИ НА ОСНОВЕ ТЕОРИИ СЛУЧАЙНЫХ ФУНКЦИЙ

Рассматриваемый метод отличается от нейросетевого подхода тем, что в его основу заложена теория случайных функций (далее СФ). С

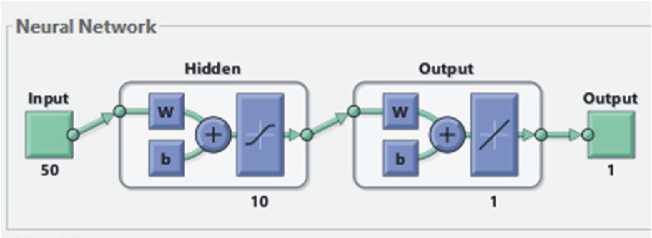
Рис. 8. Структура НС

^^ ^^ ^^ ^^ ^^ ^^ ^^ ^^ ^^ V"^1

0.8 -

0.7 -

0.6 -

0.5 -

0.4 -

0.3 -

0.2 -

0.1 -

0 L

2     4     6     8    10    12    14    16    18    20

Рис. 9. Результат работы НС на тестовой выборке: X - результат НС; • - данные тестовой выборки

Таблица 1. Матрица ошибок классификации нейронной сети при 10 нейронах

Результаты распознавания НС Самолет Вертолет Реальный объект Самолет 8 (80%) 2 (20%) техники Вертолет 0 (0%) 10 (100%) его помощью можно получить точное решение не только задачи классификации, но и многомерной интерполяции и аппроксимации, гарантирующее оптимальность. Метод довольно прост и сводится к системе линейных уравнений, и подробно описан в публикациях [5-7].

При решении задачи классификации, многомерной интерполяции и аппроксимации предполагается, что искомая функция является реализацией некоторой случайной функции, которая удовлетворяет обучающей выборке. Эта идея является основой данного метода.

Работу метода можно описать следующим образом. Пусть последовательность представляет собой набор входных векторов для обучения, соответствующие им представляют собой набор выходных значений. Метод позволяет определить функцию (2), связывающую значения на входе и на выходе (которая будет являться наиболее вероятной реализацией случайной функции)

/Ч*) = q_xK_f(x- ^ + ч_гК^х-х^ + -

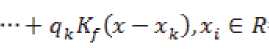
Функция определяется выражением (3)

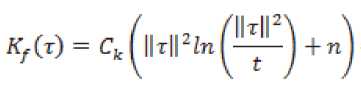
где , t, n – коэффициенты,    – норма векто ра τ.

Коэффициенты          вычисляются из системы линейных уравнений r q 1 \Kf (Xi - xj + 5^(xjj + q^(4-^2)+ - + Чкк/(х1-хк) = У1#

,      (4)

Vq1Kf(xk-x1) + q2Kf(xk-x2) + ... + qk(Kf(xk -xk) + S^(x2)) = yk### где – среднеквадратичное отклонение для шума в точке x.

Значения определяют априорно предполагаемый уровень шума (погрешности) в данных обучения и соответственно степень приближения, с которой функция (2) воспроизведет данные обучения. В выражении (3) коэффициенты t и n в «идеальном случае» должны быть приблизительно равны и устремлены в бесконечность, «каллибровочный» коэффициент связан со свойствами априорной случайной функции.

Применяя данный метод для рассматриваемой задачи, были получены результаты, представленные на рис. 10.

Исследована ошибка классификации данно-

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1 -

0 L

wwwYYW•YУ '

2     4     6     8    10    12    14    16    18    20

Рис. 10. Результат работы метода классификации на основе теории СФ на тестовой выборке: X - результат НС; • - данные тестовой выборки

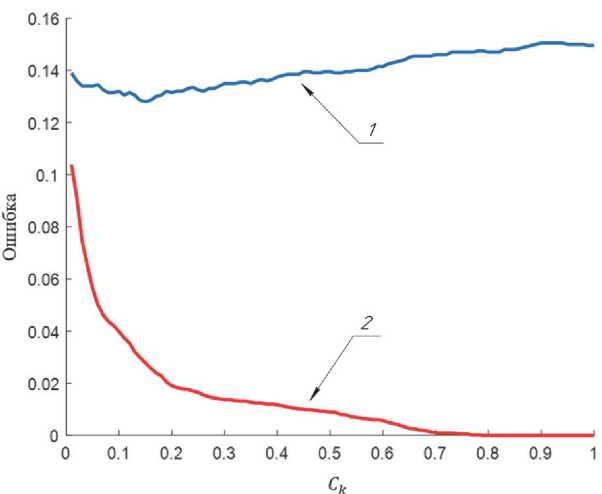
Рис. 11. Ошибка метода классификации на основе СФ на тестовой и обучающей выборке: 1 – тестовая выборка; 2 – обучающая выборка

Таблица 2. Матрица ошибок классификации метода на основе СФ при = 0,2

Результаты распознавания НС Самолет Вертолет Реальный объект Самолет 9 (90%) 1 (10%) техники Вертолет 1 (10%) 9 (90%) го метода при различных обучающих и тестовых выборках и значениях «каллибровочного» коэффициента , которая приведена на рис. 11.  1.

Как показывают результаты, минимальная   .

ошибка на тестовой выборке достигается при равном 0,2. Также можно заметить, что при увеличении ошибка классификации на тестовой выборке сначала уменьшается, а затем возрастает.

Ошибка классификации объектов (вертолет, самолет) на тестовой выборке представлена в табл. 2.

Как можно увидеть, ошибка классификации ^2. на основе теории СФ устойчива при различных тестовых и обучающих выборках по сравнению с ошибкой класификации НС. Время обучения при классификации НС больше. Также можно заметить, что при увеличении «каллибровоч-ного» коэффициента, ошибка классификации метода на основе теории СФ на обучающей выборке стремится к нулю, а ошибка классифика- 3. ции при помощи НС на обучающей выборке не достигает нулевого значения.

При тестировании метода классфикации на основе теории СФ было замечено, что при большой обучающей выборке не хватало мощностей 4. вычислительной машины для решения систем уравнений большой размерности, но в расма-триваемой задаче выборка небольшая, поэтому данная проблема не возникла.

ЗАКЛЮЧЕНИЕ

В данной работе был рассмотрен и приме-  5

нен информативный признак - отсчеты оценок . СПМ. Также проведена нейросетевая классификация и классификация методом на основе теории СФ реализации сигналов «вертолет», «самолет» с применением данного признака. Для поставленной задачи была разработана про-  6.

грамма в среде MATLAB, которая выполняет предварительную обработку звуковых файлов, выделение информативного признака сигнала, создание базы данных для обучения и тести-  7.

рования НС, а также для тестирования метода классификации на основе теории СФ. Результаты показали, что программа выполняет классификацию с хорошей точностью. В разработанной программе ошибка классификации метода 8. на основе СФ устойчива и стремится к нулю по сравнению с ошибкой классификации НС.