Применение обобщенного метода точечных источников поля для решения краевых задач математической физики
Автор: Князев Сергей Юрьевич, Щербакова Елена Евгеньевна
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Механика
Статья в выпуске: 2 (89) т.17, 2017 года.
Бесплатный доступ
Введение. Целью работы является разработка нового универсального численного метода решения краевых задач для линейных уравнений эллиптического типа. Материалы и методы. Предложенный метод основан на приведении исходного уравнения математической физики к более простому неоднородному уравнению с известным фундаментальным решением. Затем предлагается произвести переход к неоднородному интегральному уравнению с ядром, выражаемым через известное фундаментальное решение. Полученное интегральное уравнение совместно с граничными условиями решается численно. В результате было получено искомое приближенное решение, потенциал поля в аналитическом виде, что позволило не только находить приближенное значение потенциала поля в любой точке области решения, но и дифференцировать этот потенциал, причем без заметной потери точности. Это свойство разработанного численного метода выгодно отличает его от традиционных численных методов решения краевых задач, таких, например, как метод конечных элементов. Результаты исследования. Для подтверждения эффективности предложенного численного метода решена двумерная и трехмерная краевые задачи с известными решениями. Получены зависимости погрешности численного решения от числа линейных уравнений в результирующей системе. Показано, что даже при небольшом числе уравнений в системе (порядка нескольких сотен) достигается точность решения на уровне сотых долей процента. Еще одной важной иллюстрацией эффективности предложенного метода является решение квантово-механической задачи для одномерного и двумерного квантового осциллятора. Показано, что рассматриваемый метод позволяет находить собственные значения энергии и собственные функции с приемлемой точностью. Разработанный численный метод позволяет существенно расширить область применения традиционного метода точечных источников поля при решении прикладных задач моделирования полей различной физической природы, включая задачи на собственные значения. Обсуждение и заключения. Полученные результаты подтверждают, что физическое поле, описываемое практически любым линейным уравнением эллиптического типа, можно представить в виде суперпозиции полей точечных источников, удовлетворяющих более простому уравнению, решение которого находится с помощью метода точечных источников поля. Таким образом, представленный в данной работе численный метод можно рассматривать как обобщенный метод точечных источников поля.
Фундаментальное решение, метод фундаментальных решений, метод точечных источников, уравнения эллиптического типа, краевая задача
Короткий адрес: https://sciup.org/14250275
IDR: 14250275 | УДК: 539.182; | DOI: 10.23947/1992-5980-2017-17-2-12-22
Текст научной статьи Применение обобщенного метода точечных источников поля для решения краевых задач математической физики
Введение. Целью работы является разработка нового универсального численного метода решения краевых задач для линейных уравнений эллиптического типа.
Материалы и методы. Предложенный метод основан на приведении исходного уравнения математической физики к более простому неоднородному уравнению с известным фундаментальным решением. Затем предлагается произвести переход к неоднородному интегральному уравнению с ядром, выражаемым через известное фундаментальное решение. Полученное интегральное уравнение совместно с граничными условиями решается численно. В результате было получено искомое приближенное решение, потенциал поля в аналитическом виде, что позволило не только находить приближенное значение потенциала поля в любой точке области решения, но и дифференцировать этот потенциал, причем без заметной потери точности. Это свойство разработанного численного метода выгодно отличает его от традиционных численных методов решения краевых задач, таких, например, как метод конечных элементов.
Результаты исследования . Для подтверждения эффективности предложенного численного метода решена двумерная и трехмерная краевые задачи с известными решениями. Получены зависимости погрешности численного решения от числа линейных уравнений в результирующей системе. Показано, что даже при небольшом числе уравнений в системе (порядка нескольких сотен) достигается точность решения на уровне сотых долей процента. Еще одной важной иллюстрацией эффективности предложенного метода является решение квантово-механической задачи для одномерного и двумерного квантового осциллятора. Показано, что рассматриваемый метод позволяет находить собственные значения энергии и собственные функции с приемлемой точностью. Разработанный численный метод позволяет существенно расширить область применения традиционного метода точечных источников поля при решении прикладных задач моделирования полей различной физической природы, включая задачи на собственные значения.
Обсуждение и заключения. Полученные результаты подтверждают, что физическое поле, описываемое практически лю-
Introduction. The work objective is to develop a new universal numerical method for solving boundary value problems for linear elliptic equations.
Materials and Methods . The proposed method is based on the transformation of the original mathematical physics equation to a simpler inhomogeneous equation with the known fundamental solution. From this equation, the transition to an inhomogeneous integral equation with the kernel expressed by the known fundamental solution is carried out. The obtained integral equation with boundary conditions is solved numerically. An approximate solution, the field potential being in an analytical form, is resulted. That allows not only find an approximate value of the field potential at any point in the solutions domain, but also differentiate this potential, and all without perceptible loss of accuracy. This property of the developed numerical method sets it apart from the traditional numerical methods for solving boundary value problems, such as the finite element method.
Research Results . To confirm the effectiveness of the proposed numerical method, the two-dimensional and three-dimensional boundary value problems with the known solutions are solved. The dependences of the numerical solution error on the number of linear equations in the resulting system are obtained. It is shown that even at a small number of equations in the system (some hundreds) the solution accuracy is achieved at the level of hundredths of a percent. Another major illustration of the proposed method effectiveness is the solution to quantum mechanical problems for the one-dimensional and twodimensional quantum oscillators. It is shown that the given method allows finding the energy eigenvalues and eigenfunctions with an acceptable accuracy. The developed numerical technique allows greatly extend the application domain of the traditional point source method in solving applied problems for modeling fields of different physical nature, including the eigenvalue problems.
Работа выполнена в рамках инициативной НИР.
∗∗∗ The research is done within the frame of independent R&D.
бым линейным уравнением эллиптического типа, можно представить в виде суперпозиции полей точечных источников, удовлетворяющих более простому уравнению, решение которого находится с помощью метода точечных источников поля. Таким образом, представленный в данной работе численный метод можно рассматривать как обобщенный метод точечных источников поля.
Discussion and Conclusions. The results obtained confirm that a physical field described by any linear elliptic equation can be represented as a superposition of point source fields satisfying a simpler equation, the solution of which is obtained through the method of point source of the field. Therefore, the numerical method presented in this paper can be considered as a generalized point source method.
Введение. Основными методами численного решения краевых задач для уравнений математической физики в настоящее время являются метод конечных элементов (МКЭ) и, в значительно меньшей степени, метод конечных разностей (МКР). Эти методы могут использоваться при решении практически любых линейных уравнений, что позволяет считать МКЭ и МКР универсальными методами решения краевых задач. Область применения других методов обычно ограничивается вполне определенными типами уравнений математической физики. Тем не менее, методам МКЭ и МКР присущи определенные недостатки. Это, например, недостаточно быстрая сходимость численного решения с уменьшением шага разностной сетки и обусловленная этим высокая погрешность результата. Определенные трудности возникают, если граничные условия содержат производную по нормали от искомой функции. Если кроме искомой функции необходимо определить и ее производные, то для этого необходимо производить численное дифференцирование, что также ведет к появлению дополнительной, весьма значительной погрешности. В связи с этим проблема поиска новых численных методов решения краевых задач продолжает оставаться актуальной.
Одним из эффективных методов решения краевых задач, который может являться альтернативой МКЭ и МКР, является метод точечных источников поля (МТИ) [1–5]. Этот метод может использоваться для решения широкого круга задач математической физики. Наиболее эффективно использование этого метода при решении краевых задач для уравнений эллиптического типа: Лапласа, Гельмгольца, бигармонического уравнения [6–12]. Имеются сведения о возможности и эффективности использования этого метода при решении краевых задач для уравнений параболического типа, для волновых уравнений [13–15], при моделировании полей упругих напряжений в деформированных твердых телах [16–20] и т. д.
Для МТИ характерны высокое быстродействие в сочетании с малой вычислительной погрешностью, а также простота компьютерной реализации. Для возможности использования МТИ необходимо располагать фундаментальными решениями исходного уравнения в аналитическом виде. Однако при решении некоторых задач математической физики фундаментальные решения неизвестны, что является препятствием для использования МТИ. Тем не менее, как показано в [21–22], имеется возможность получения фундаментальных решений численно, с последующим их применением в МТИ. С помощью подхода, используемого в [23–24], искомое решение краевой задачи было получено без предварительных вычислений фундаментальных решений. Это позволило значительно расширить область применения МТИ.
Интегральные уравнения для численного решения краевой задачи. Пусть в области Ω фундаментальное решение g ( r , R ) уравнения LU = 0 известно. Требуется найти решение краевой задачи для неоднородного уравнения ( L + l ( r ) ) U ( r ) = f ( r ) , r eQ , (1)
с условиями на границе ∂Ω:
Л( r) U (r ) = ф( r), r edQ , (2)
где L , l ( r ) , Л ( r ) — линейные операторы в области О и на границе дО.
Для определенности будем считать, что операторы l ( r ) и Л ( r ) имеют вид:
l (r ) = a (r) + B (r )-V , r eQ ,dЛ(r) = a(r) + в(r)—, r edQ .
Здесь a ( r ) , B ( r ) , a ( r ) , P ( r ) — заданные скалярные и векторная функции в области О и на границе дО, V — оператор Гамильтона.
Ищем решение задачи (1)–(2) в виде:
U (r ) = и (r) + v (r), где функция v (r) удовлетворяет однородному уравнению
Lv = 0 , (3)
а неизвестная функции u ( r ) есть частное решение уравнения
Lu = f -1 (r) u -1 (r) v (r), правую часть которого f -1 (r)u -1 (r)v = p(r) можно рассматривать как плотность р(r) некоторого фиктивного заряда, распределенного в области О. Отсюда для функции u (r) получаем интегральное уравнение u (r) = Jg(r,R)p(R)dQr или u (r ) = J g (r,R)(f (R)-1 (R) v (R)-1 (R) u (R)) dQ R. (4)
q
Для функции v ( r ) , как в МТИ, используется приближенное выражение
Nq v (r )=Z qkg (r, Pk). (5)
k = 1
Здесь Nq — число точечных зарядов qk , моделирующих поле, располагаемых в точках с координатами ρ k за пределами области решения задачи Ω, вблизи ее границы.
Теперь уравнение (4) принимает вид:
Nq u (r ) = J g (r,R)| f (R)-1 (R )Z qkg (R, Pk)-l (R) u (R )I dQ R. (6)
Q V k = 1 7
Если оператор 1 ( R ) представляет собой скалярную функцию (это справедливо, если решается, например, стационарное уравнение Шредингера), то, вычисляя интеграл в правой части соотношения (6) численно, можно, как будет показано ниже, построить алгоритм для нахождения значений функции u ( r ) в узловых точках области О. В более общем случае подействуем на уравнение (6) оператором 1 ( r ) . Введя при этом новую функцию w ( r ) = 1 ( r ) u ( r ) , получим для этой неизвестной функции интегральное уравнение:
Nq w (r ) = J1 (r) g (r,R )|f (R)-w (R)-1 (R )Z qkg (R, Pk) I dQ r .
Q V k=1
Решая уравнение (7) численно находим функцию w ( r ) , после чего, используя уравнение (6), записанное в виде
Nq u (r ) = J g (r,R )|f (R)-1 (R )Z qkg (R Pk)-w (R) I dQ r ,(8)
Q V k=1
находим искомую функцию u ( r ) .
Пусть теперь r e dQ . Подействуем на уравнение (8) при r е dQ оператором Л ( r ) :
Nq
Л( r ) u ( r ) = J Л( r ) g ( r ,R ) | f ( R )- 1 ( R ) Z q k g ( R , P k )- w ( R ) I d Q R .
Q V k=1
Теперь граничное условие (2) можно записать в виде:
NqNq
JЛ(r)g(r,R)| f (R)-1 (R)Z qkg(R,Pk)- w(R) I dQR + Z qkЛ(r)g(r,Pk ) = Ф(r), r edQ .
Q V k=1 7
Соотношения (7)–(9) можно использовать для численного решения исходной краевой задачи. Построим алгоритм решения этой задачи.
Алгоритм численного решения краевой задачи . Область решения Ω разбивается на элементарные участки площадью (объемом), равным ω j . Число таких участков обозначим как Nu . Внутри каждого участка выбираем точку, узел с координатой R j . Некоторые из точек, узлов r k = R j , число которых N G =N q , располагаются на границе области решения. Теперь уравнение (7) принимает вид:
NuNuNq w (r )+Z1 (r) g (r,Rj) w (Rj^toj = z|f (Rj )-Z qk1 (R) g (Rj, Pk )I l (r) g (r,R j )®j.
-
j=1 j=1V k=1
Это уравнение должно выполняться во всех N u узловых точках, включая N G граничных узлов. Запишем уравнение (10) для каждого узла R i . Получим:
Nu Nu w (Ri) + Z 1 (Ri) g (Ri,Rj^ w (Rj)®y = Z 1 (Ri) g (Ri,Rj-)| f (Rj-)-Z qJ (Rj) g (Rj, Pk )I®j-.
-
j=1 j=1 V k=1
В результате получаем N u уравнений для N u + N G неизвестных. Это N u значений функции w ( r ) в N u узловых точках R i , и N q = N G зарядов q k , располагаемых в точках с координатами ρ k . Для получения замкнутой системы уравнений необходимо дополнить систему (11) уравнениями, учитывающими граничные условия для решаемой задачи. Для этого используем интегральное уравнение (9).
На границе ∂Ω, в точках с координатами r m располагаем граничные узловые точки, количество которых равно N q = N G . Заменяем приближенно интегралы в (9) интегральными суммами, как это сделано при получении соотношений (10), (11). В результате для каждого граничного узла получим уравнение:
Nu Nq Nq
Z Л( r m ) g ( rm,Rj ) \ f ( Rj ) -Z q k l ( R j ) g ( Rj , P k ) — w ( R j ) |® j + Z q k Л( r m ) g ( r m ,P k ) = Ф( r m ) • (12) j = 1 V k = 1 / " k = 1
Решая объединенную систему уравнений (11), (12) находим Nu значений функции w(r) в узловых точках области Ω, и NG значений точечных зарядов qk. Затем с помощью соотношения (8) вычисляем приближенное значение функции u (r) в произвольной точке области Q, и, обозначив w(Rj) как wj, а f (Rj) как fj, получаем искомое ре- шение исходной задачи в виде соотношения:
Nu Nq Nq
U ( r ) = Z g ( Г.R j ) I f - l ( R j ) Z Q k g ( R j ,P k ) - w j 7) ■ Z q k g ( r, P k ) . (13)
j = 1 V k = 1 7 k = 1
Следует обратить внимание на то, что соотношение (13) дает приближенное аналитическое выражение для искомой функции U ( r ) . Это значит, что с полученным решением U ( r ) можно поступать как с любым другим аналитическим выражением. Его можно дифференцировать, интегрировать, производить другие действия, и при этом не возникает дополнительная численная погрешность. Например, частную производную по координате х от функции U ( r ) можно вычислить с помощью формулы:
д U ( r ) д x
Z д g ( r.R ) j = 1 д x
д g ( r. P k ) д x
Аналогичным образом можно получить аналитические выражения для вычисления результатов других математических операций над функцией U ( r ) .
Решение тестовых задач. Ниже приводятся результаты решения тестовых задач, подтверждающих эффективность рассматриваемого метода при решении краевых задач для уравнений эллиптического типа. Сначала решалась двумерная краевая задача. В области Ω, представляющей собой квадрат со стороной L=2, центр которого совме- щен с началом координат, решалась задача для уравнения
A U ( r ) + 2 y 2
д U ( r ) + x 2 д x
д U ( r ) д y
+ sin ( xy ) U ( r ) = f ( r ) , r eQ
с условиями на границе ∂Ω
U ( r ) + xy ^ U ^ = ф ( r ) , r eдQ . v ’ 4 д n
Функции f ( r ) и ф ( r ) в соотношениях (15), (16) подбирались таким образом, чтобы они соответствовали точному решению краевой задачи (15)–(16) в виде:
U ( r ) = U ( x , y ) = x 2 + y + sin ( xy ) . (17)
При решении краевой задачи оператору L в уравнении (1) соответствовал двумерный оператор Лапласа L =Δ и, соответственно, фундаментальное решение g ( r , R ) имело вид:
g ( r , R ) = ;1ln r - R I.
2 n
2 д 2 д
Оператору l (r) в (1) соответствовал оператор l (r) = 2y--+ x2--+ sin (xy), а оператору Л( r) в (2) — оператор дx дy xy д
Л ( r ) = 1 + —--.
v ’ 4 д n
При численном решении краевой задачи (15)–(16) задавалось число N 0 , определяющее равномерный шаг h сетки в области решения Ω. Точечные заряды q k , моделирующие поле, равномерно располагались по периметру квадрата со стороной Lq=kL . Параметр k >1 определял удаленность зарядов от границ области решения. При этом слишком большое и слишком малое удаление зарядов, как и в стандартном варианте МТИ, нежелательны, так как это ведет к снижению точности решения задачи. Авторами при вычислениях использовалось k =1,3. Полное число узлов в области
Ω равнялось N u =N 0 2, а количество точечных зарядов, моделирующих поле N q =4( N 0 –1). Таким образом, полное число уравнений в системе (11)–(12) составило Nn =Nu +Nq = N 02+4( N 0–1).
После нахождения приближенного численного решения краевой задачи UN (r), при заданном полном числе уравнений N=Nn в системе (11)–(12), оценивалась максимальная относительная погрешность решения εmax. Для этого в области решения задачи случайным образом задавались координаты zi точек, число которых полагалось равным Nε=100, после чего относительная погрешность вычислялась с помощью формулы max UN (z,-)- U (z)|
max
U max где Umax — максимальное по абсолютной величине значение точного решения (17) в области Ω. Аналогичным образом, наряду с максимальной относительной погрешностью оценивалась и среднеквадратичная погрешность.
Количество узлов
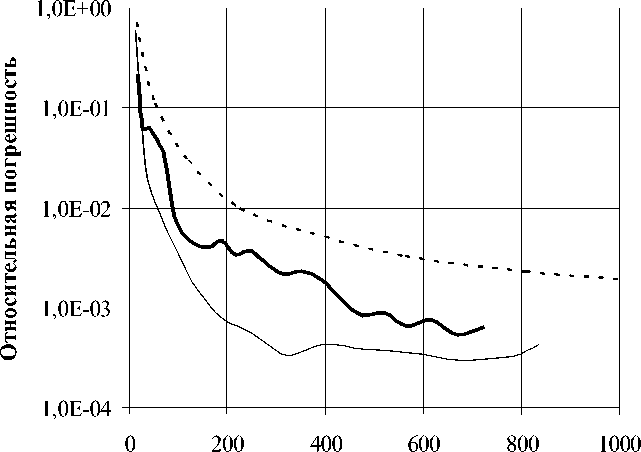
Рис. 1. Зависимость максимальной относительной погрешности численного решения от количества узлов при решении двумерной и трехмерной краевой задачи
Fig. 1. Dependence of maximum relative error of numerical solution of the number of nodes under solving two-dimensional and the three-dimensional boundary value problem
На рис. 1 представлена зависимость максимальной относительной погрешности от полного числа уравнений N=Nn в системе (11)–(12) (жирная сплошная линия). С ростом числа N от начального значения N =17 до значения N =721 погрешность решения уменьшается более чем на два порядка, от εmax=2,1∙10–1 до εmax=7,5∙10–4.
Для получения системы (11)–(12) использовался простейший метод численного интегрирования, аналог метода прямоугольников. Можно предположить, что использование более точного метода численного интегрирования позволит повысить точность решения краевой задачи. Действительно, использование метода Гаусса с третьим порядком интегрирования позволило повысить точность численного решения почти на порядок. Это проиллюстрировано рис. 1, где тонкая сплошная линия представляет зависимость погрешности решения краевой задачи от числа уравнений N , рассчитанной при использовании метода Гаусса.
Далее решалась трехмерная задача Дирихле. В области Ω, представляющей собой куб со стороной L =2, центр которого совмещен с началом координат, решалась задача для уравнения
d U (r) ,3 U (r) d U (r)
A U (r) + 2 y2---- ■ x2---- ■---- ■ sin (xy) U (r ) = f (r), r eQ . (18)
d x d y d z
Функции f ( r ) в уравнении (18) и в правой части условия Дирихле подбирались таким образом, чтобы они соответствовали точному решению краевой задачи в виде:
U ( r ) = U ( x , y , z ) = x 2 + y + sin ( xy ) - z . (19)
При решении краевой задачи оператору L в уравнении (1) соответствовал трехмерный оператор Лапласа L =Δ и, соответственно, фундаментальное решение g ( r , R ) имело вид
g ( r , R ) = — 4n| r - R'
d i00
Оператору l(r) в (1) соответствовал оператор l(r) = 2y--+ x2--1---+ sin(xy), а оператору Л(r) в (2) соответ- x 0y 0z ствовал оператор Л( r) = 1.
Пунктирная кривая на рис. 1 представляет зависимость относительной погрешности решаемой задачи Дирихле от размерности N , т. е. от числа уравнений в системе (11)–(12), для решения которой использовался аналог метода прямоугольников. Видно, что уже при относительно небольшой размерности численной задачи N =800 погрешность решения составляет εmax=2,0∙10–3. Можно предположить, что и в этом случае использование более точного метода численного интегрирования позволит снизить погрешность решения краевой задачи.
Решение стационарного уравнения Шредингера. Фундаментальное значение при решении квантовомеханических задач имеет уравнение Шредингера [25]. Аналитические решения этого уравнения могут быть получены лишь для весьма ограниченного круга задач, преимущественно одномерных. Несмотря на широкий спектр имеющихся численных методов решения уравнения Шредингера, проблема эффективных способов нахождения собственных энергий и собственных функций для основного уравнения квантовой механики, особенно при решении многомерных задач, продолжает оставаться актуальной [23–24]. Предложенный численный метод может, в ряде случаев, использоваться при решении квантово-механических задач.
Пусть частица массой т совершает финитное движение в силовом поле V (r). Запишем стационарное урав- нение Шредингера в виде:
Ау + 2^-Eу = 2mV(r)у .
Необходимо, решая уравнение (20), найти собственные значения энергии Е и соответствующие им собственные функции, волновые функции частицы у ( r ) .
При решении краевой задачи для уравнения Шредингера оператору L в уравнении (1) соответствует оператор
2 m 2 m
Лапласа L =Д, а оператор l ( r ) в (1) есть скалярная функция l ( r ) = E - -2- V ( r ) .
При реализации алгоритма решения уравнения Шредингера сначала задается энергия частицы E . Область решения для уравнения Шредингера Ω берется близкой, но несколько большей классически доступной для частицы области движения, границы которой определяются уравнением
V (r ) = E.
Размеры области Ω подбираются таким образом, чтобы на ее границах волновая функция с заданной точностью равнялась нулю. Для получения нетривиального решения задается некоторая точка М внутри области Ω, например, на границе классически допустимой области движения, в которой значение волновой функции заведомо не равняется нулю. В этой точке значение волновой функции полагается равным единице: у ( M ) = 1. После получения решения волновую функцию можно легко перенормировать.
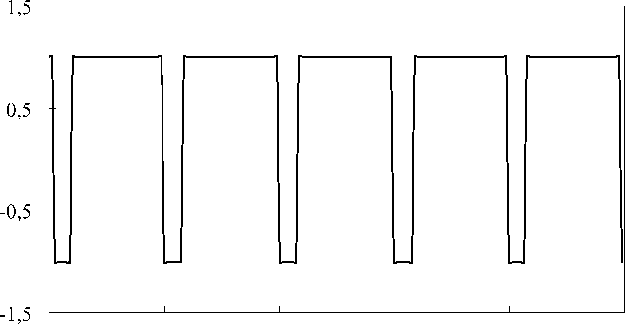
После численного решения задачи описанным выше способом проверяется найденное значение волновой функции в точке G. Если окажется, что с достаточной точностью выполняется условие у (G) = 0, то это означает, что заданное значение энергии E является собственным значением, а найденная волновая функция у(r) является собственной функцией для данной энергии E. В противном случае подбираются такие два значения энергии E1 и E2> E1 при которых у( G) имеет различные знаки. После этого собственное значение энергии в интервале (E 1, E2) и собственная функция находятся, например, с помощью метода половинного деления. Иллюстрацией такого подхода является рис. 2, на котором представлен график зависимости функции sign (у (G)) от значения квантового числа n для одномерного квантового осциллятора.
Квантовое число n
Рис. 2. Зависимость знака волновой функции в граничной точке G от значения квантового числа n
Fig. 2. Dependence of wave function sign at boundary point G on the value of quantum number n
Как известно, собственные значения одномерного квантового осциллятора определяются выражением
E = Atof n + ^j, где ю — частота осциллятора, а квантовое число n принимает целочисленные значения, начиная с нуля. Как продемонстрировано на рис. 2, вблизи целочисленных значений n знак у (G) изменяется с положительного (при меньших n) на отрицательное (при больших n). Вблизи такого перехода можно подобрать значение n=nN, при котором у(G) с приемлемой точностью равняется нулю. Величина An отклонения nN от целочисленного значения определяет погрешность для численного значения собственной энергии.
На рис. 2 также изображены переходы от отрицательных значений у ( G ) к положительным. По мере приближения к такому переходу значение у ( G ) резко возрастает по абсолютной величине, но не обращается в ноль. Поэтому такие переходы не соответствуют собственным значениям энергии.
Точность в определении собственных значений энергии увеличивается с ростом размерности N системы линейных уравнений, к которой приводится численная задача для уравнения Шредингера. Наибольшая точность, естественно, наблюдается при решении одномерной задачи Шредингера. Например, относительная погрешность Δ E при вычислении первого собственного значения энергии одномерного осциллятора изменялась от значения 0,15 при N =20 до значения 0,00025 при N =120. При решении двумерных и трехмерных задач точность вычислений значительно снижается. На рис. 3 представлены зависимости относительной погрешность Δ E для собственных значений энергии двумерного осциллятора от размерности N численной задачи. Жирная сплошная линия на рис. 3 соответствует основному, нулевому энергетическому уровню, тонкая сплошная линия — второму энергетическому уровню, пунктирная линия — четвертому энергетическому уровню. При решении двумерной задачи относительная погрешность порядка нескольких процентов легко достижима. Можно ожидать, что использование более точного метода численного интегрирования, как и в предыдущем случае, позволит повысить точность численного решения квантово-механической задачи.
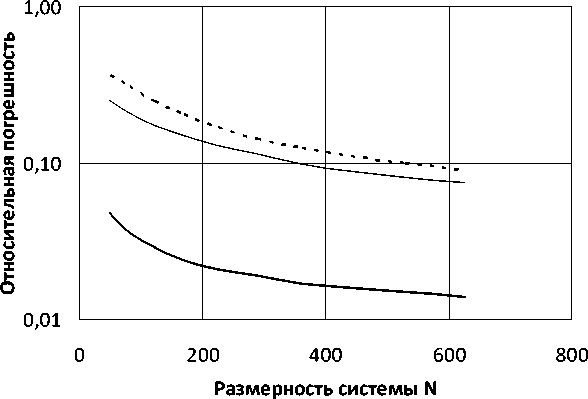
Рис. 3. Зависимость относительной погрешности от размерности системы уравнений для трех собственных значений энергии двумерного осциллятора
Fig. 3. Dependence of relative error on dimensionality of system of equations for three energy eigenvalues of two-dimensional oscillator
Описанный алгоритм численного решения стационарных квантово-механических задач не зависит от их размерности. Решение может несколько усложниться при наличии вырождения энергетических уровней, когда одному собственному значению энергии соответствует несколько собственных функций. Например, при решении задачи для двумерного квантового осциллятора собственные значения энергии определяются двумя квантовыми числами nx и ny: E = Ex + Ey = Йю( nx + ny +1). При численном решении краевой задачи область решения О, в соответствии с (21), зада- ется в виде прямоугольника, несколько большего классически доступной для частицы области движения, с соотноше-
L нием сторон х^= =
I nx + 1/2 n y + 1/2
. Отсюда следует, что, например, первый энергетический уровень с n = n x + n y = 1 два-
жды вырожден. Этому энергетическому уровню соответствуют две собственные функции, рассчитываемые при
y
При другом соотношении сторон по-
n = 1, n = 0 и n = 0, n = 1, и при соотношении сторон — xy xy Ly лучается смешанное состояние.
Заключение. Полученные результаты показывают, что физическое поле, описываемое практически любым линейным уравнением эллиптического типа ( L + l ( r ) ) U ( r ) = f ( r ) можно представить в виде суперпозиции полей точечных источников, удовлетворяющих более простому уравнению LU ( r ) = f ( r ) , решение которого находится с помощью МТИ. Поэтому разработанный численный метод можно рассматривать как обобщенный метод точечных источников поля (ОМТИ). Решение тестовых задач подтверждает эффективность ОМТИ при решении достаточно сложных краевых задач, включая трехмерные задачи и задачи на собственные значения, в том числе квантовомеханические. Существенным преимуществом ОМТИ по сравнению с традиционными методами численного решения краевых задач, таких как МКР или МКЭ, является возможность получения решения в аналитическом виде, что позволяет производить с этим решением соответствующие математические операции без потери точности. Численные эксперименты показали, что погрешность для производных по координатам имеет тот же порядок точности, что и погрешность для искомого потенциала.
Список литературы Применение обобщенного метода точечных источников поля для решения краевых задач математической физики
- Fairweather G. The method of fundamental solutions for elliptic boundary value problems/G. Fairweather, A. Karageorghis//Ad. Vol. Comput. Math. -1998. -Vol. 9. -P. 69-95.
- Alves C.J.S. A new method of fundamental solutions applied to nonhomogeneous elliptic problems/C.J.S. Alves, C.S. Chen//Advances in Computational Mathematics. -2005. -Vol. 23 -P. 125-142.
- Бахвалов, Ю. А. Погрешность метода точечных источников при моделировании потенциальных полей в областях с различной конфигурацией/Ю. А. Бахвалов, С. Ю. Князев, А. А. Щербаков, Е. Е. Щербакова//Известия высших учебных заведений. Электромеханика. -2012. -№ 5. -С. 17-21.
- Князев, С. Ю. Сравнительный анализ двух вариантов метода коллокаций при численном моделировании потенциальных полей/С. Ю. Князев, Е. Е. Щербакова, А. Н. Заиченко//Известия высших учебных заведений. Электромеханика. -2014. -№ 1. -С. 17-19.
- Князев, С. Ю. Компьютерное моделирование потенциальных полей методом точечных источников/С. Ю. Князев, Е. Е. Щербакова, А. А. Щербаков. -Ростов-на-Дону: Издательский центр ДГТУ, 2012. -156 с.
- Князев, С. Ю. Устойчивость и сходимость метода точечных источников поля при численном решении краевых задач для уравнения Лапласа/С. Ю. Князев//Известия высших учебных заведений. Электромеханика. -2010. -№ 1. -С. 3-12.
- Князев, С. Ю. Решение трехмерных краевых задач для уравнений Лапласа с помощью метода дискретных источников поля/С. Ю. Князев, Е. Е. Щербакова//Известия высших учебных заведений. Электромеханика. -2015. -№ 5. -С. 25-30.
- Князев, С. Ю. Численное решение краевых задач для уравнения Пуассона методом точечных источников поля/С. Ю. Князев, Е. Е. Щербакова, А. А. Енгибарян//Вестник Дон. гос. техн. ун-та. -2014. -Т. 14, № 2 (77). -С. 15-20.
- Князев, С. Ю. Численное решение уравнений Пуассона и Гельмгольца с помощью метода точечных источников/С. Ю. Князев//Известия высших учебных заведений. Электромеханика. -2007. -№ 2. -С. 77-78.
- Князев, С. Ю. Численное решение краевых задач для неоднородных уравнений Гельмгольца методом точечных источников поля/С. Ю. Князев, Е. Е. Щербакова, А. Н. Заиченко//Известия высших учебных заведений. Электромеханика. -2014. -№ 4. -С. 14-19.
- Князев, С. Ю. Применение метода точечных источников поля при численном решении задач на собственные значения для уравнения Гельмгольца/С. Ю. Князев, Е. Е. Щербакова//Известия высших учебных заведений. Электромеханика. -2016. -№ 3 (545). -С. 11-17.
- Щербакова, Е. Е. Решения задач на собственные значения для уравнения Гельмгольца методом точечных источников поля/Е. Е. Щербакова//Вестник Дон. гос. техн. ун-та. -2016. -Т. 16, № 3 (86). -С. 87-95.
- Князев, С. Ю. Решение задач тепло-и массопереноса с помощью метода точечных источников поля/С. Ю. Князев, Е. Е. Щербакова//Известия высших учебных заведений. Северо-Кавказский регион. Серия: Технические науки. -2006. -№ 4. -С. 43-47.
- Князев, С. Ю. Численное исследование стабильности термомиграции плоских зон/С. Ю. Князев, Е. Е. Щербакова//Известия высших учебных заведений. Электромеханика. -2007. -№ 1. -С. 14-19.
- Лунин, Л. С. Исследование стабильности термомиграции ансамбля линейных зон с помощью трехмерной компьютерной модели, построенной на основе метода точечных источников поля/Л. С. Лунин, С. Ю. Князев, Б. М. Середин, А. С. Полухин, Е. Е. Щербакова//Вестник Южного научного центра. -2015. -Т. 11, № 4. -С. 9-15.
- Liviu Marin The MFS-MPS for two-dimensional steady-state thermoelasticity problems/Liviu Marin, Andreas Karageorghis//Eng. Anal. Bound. Elem. -2013. -Vol. 37. Iss. 7-8. -P. 1004-1020.
- Yan Gu Improved singular boundary method for elasticity problems/Yan Gu, Wen Chen, Xiaoqiao He//Comput. & Structures. -2014. -Vol. 135. -P. 7-82.
- Князев, С. Ю. Моделирование полей упругих деформаций с применением метода точечных источников/С. Ю. Князев, В. Н. Пустовойт, Е. Е. Щербакова//Вестник Дон. гос. техн. ун-та. -2015. -Т. 15, № 1 (80). -С. 29-38.
- Князев, С. Ю. Моделирование трехмерных полей упругих деформаций с помощью метода точечных источников/С. Ю. Князев, В. Н. Пустовойт, Е. Е. Щербакова, А. А. Щербаков//Вестник Дон. гос. техн. ун-та. -2015. -Т. 15, № 4 (83). -С. 13-23.
- Князев, С. Ю. Математическое моделирование полей упругих деформаций методом точечных источников поля/С. Ю. Князев, Е. Е. Щербакова, А. А. Щербаков//Математические методы в технике и технологиях. -2015. -№ 5 (75). -С. 21-23.
- Князев, С. Ю. Применение численных фундаментальных решений в методе точечных источников поля/С. Ю. Князев, Е. Е. Щербакова//Вестник Дон. гос. техн. ун-та. -2016. -Т. 16, № 4 (87). -С. 118-125.
- Князев, С. Ю. Метод численного решения стационарного уравнения Шредингера/С. Ю. Князев, Е. Е. Щербакова//Известия высших учебных заведений. Физика. -2016. -Т. 59, № 10. -С. 87-92.
- Князев, С. Ю. Интегральное уравнение для численного решения стационарных квантово-механических задач/С. Ю. Князев//Вестник Дон. гос. техн. ун-та. -2016. -Т. 16, № 3 (86). -С. 79-86.
- Ландау, Л. Д. Квантовая механика. Нерелятивистская теория/Л. Д. Ландау, Е. М. Лифшиц. -Москва: Наука, 1963. -703 с.


