Применение пакета Maple для выполнения лабораторных работ по высшей математике
Автор: Рабчук А.В., Самигуллина Р.Г.
Журнал: Теория и практика современной науки @modern-j
Рубрика: Образование и педагогика
Статья в выпуске: 5 (5), 2015 года.
Бесплатный доступ
Лабораторные работы предназначены для предварительного ознакомления студентов 1-3 курсов с пакетом Mаple: вычисление производных, интегралов, пределов, решение дифференциальных уравнений, ряды, построение графиков. Приведены индивидуальные задания по вариантам. В данных лабораторных работах использовались материалы [1] а задачи - из различных задачников, в частности [2,3].
Производная, процедура, функция, среда maple, лабораторные работы, индивидуальные задания
Короткий адрес: https://sciup.org/140266719
IDR: 140266719
Текст научной статьи Применение пакета Maple для выполнения лабораторных работ по высшей математике
Для начала дадим некоторые основные процедуры и функции: Restart - начинать с каждой новой задачи. ^ - возведение в степень, / -деление, * - умножить,
Лабораторная работа N 1.
Вычисление производных.
Оператор diff (), -параметры процедуры: функция от которой берут производную, и переменная по которой берут производную.
ПРИМЕР1 . diff (sin(x),x); < enter> ответ: cos(x)
Plot (%);< enter> график косинуса
ПРИМЕР2. Найти производную
Y= (xsina+cosa) (xcosa-sina),
Можно сначала определить функцию следующим образом
Y:=x->(x*sin(a)+cos(a)*(x*cos(a)-sin(a)) ; < enter> diff(Y(x),x) ); < enter>
Plot (%) ;< enter>
ПРИМЕР 3. y=[x] cos(10 n x)
Y: =x->floor(x)*cos(10*pi*x); < enter> diff( Y(x),x ); < enter>
Plot (%) ;< enter>
Можно использовать оператор D.
D (SIN); ОТВЕТ COS или D (sin(x)); ответ cos(x).
ПРИМЕР 4.
1 - x если x<1
«( 1 - x )(2 - x ) если x < 2
-
Y= [ x - 2 если x>2
Производная от кусочно-гладкой функции с помощью процедуры PIECEWISE (... ) в ней последний интервал не указывается
Y: =X-> PIECEWISE(X<1,1-X, X<=2, (1-X)*(2-X),-2+X); < enter>
F: =X->diff(Y(X),X) ; < enter>
F(X); < enter> plot ([Y(X),F(X)]);< enter> графики функции и производной.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
-
1 y = 8[x 3 + 5ln x + ctgx ; || y = xfx .
ln x
x ( x 2 + 1)
y = .
—+ xctgx ;
y — i
12. V1 - x 2 ;
x
2. sin x
g y = -3/ 1 + 5 cos x ;
13. y = x ;
4. y = cos 100 x ;
14 . y = ( x - 1)V( x + 1) 2 ( x - 2);
5. y = ( x^
1 - x 2 + arcsin x );
15. y = e 1/ln x ;
2 x
6. y = e
ln tg ( x /2)
;
16 y = log7cosV1 + x.
7 y = ln( x + 31 x 2 + 6).
7. ;
7 x 2
17. y e ;
y = ln4
8.
1 + sin3 x
x - 1
y = arctg 1/ x +------
2 + cos 5 x . ;
18. x ;
2 x
y 2 + 4 4 + 52 x ;
y = (cos 7 x )
;
sin9 x
;
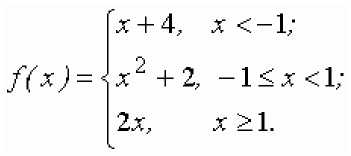
ig y = ln 5 sin x.
20 У = tg sin cos x
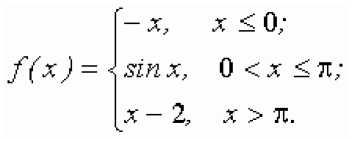
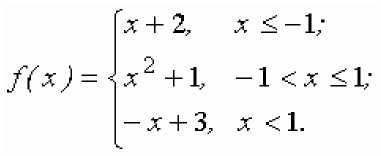
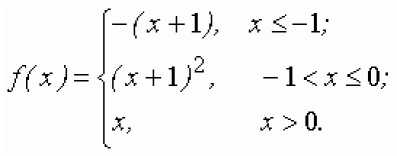
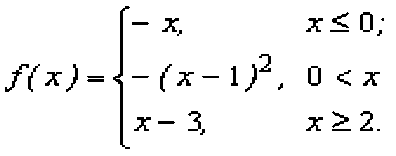
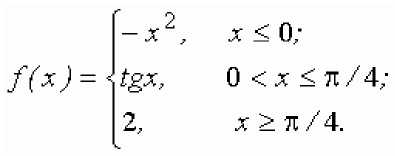
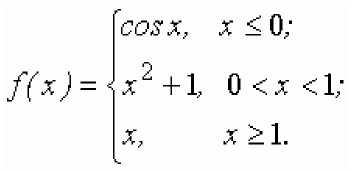
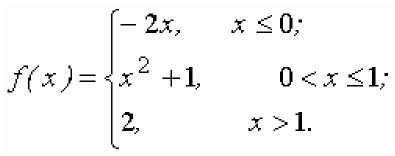
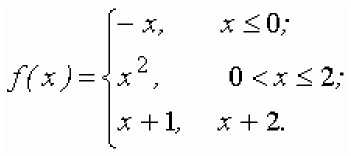
Список литературы Применение пакета Maple для выполнения лабораторных работ по высшей математике
- Васильев А.Н. Самоучитель Maple 8.:-М.: Издательский дом “Вильямс”,2003.-352с.
- Шипачев В.С. Сборник задач по высшей математике. М.,Высшая школа,1994.
- Запорожец Г.И. Руководство к решению задач по математическому анализу. Издание


