Применение PANS модели турбулентности для расчета течения в модельной радиально-осевой гидротурбине Francis-99

Отрыв и закрутка потока – самые распространённые в технических приложениях явления гидродинамики [1]. Закрученные течения широко известны в различных областях техники: горелках теплоэлектростанций, гидротурбинах, при обтекании крыла самолета, в судовых движителях и т.д. При высокой степени закрутки течение осложняется распадом вихря и формированием крупномасштабных нестационарных структур.

В гидроэнергетике проявлением неустойчивости закрученного потока выступает прецессирующий вихревой жгут в отсасывающей трубе. За рабочим колесом гидротурбины располагается отсасывающая труба, которая представляет собой расширяющийся канал, соединяющий турбину с нижним бьефом. В режиме неполной загрузки за рабочим колесом формируется – 727 – зона возвратного течения, граница которой неустойчива и сворачивается в прецессирующий вихревой жгут. Эти нестационарные длинноволновые структуры обладают значительной турбулентной кинетической энергией и характеризуются достаточно большим временем существования, что вызывает серьёзные затруднения при численном моделировании течений в тракте гидротурбин.

Инструментарий численного моделирования турбулентных течений сегодня включает широкий набор методов: от расчёта течения в отдельных элементах с помощью RANS моделей (Reynolds-Averaged Navier – Stokes – решение усреднённых по Рейнольдсу уравнений Навье – Стокса) до метода моделирования крупных вихрей (Large Eddy Simulation, LES). Тем не менее при моделировании нестационарных процессов требуются очень большие вычислительные ресурсы, что побуждает использовать некие компромиссные модели.

К сложностям, возникающим при нестационарном статистическом (URANS) моделировании закрученных течений, прежде всего нужно отнести такие особенности, отсутствующие в простых течениях, на которых выполнялась калибровка моделей. В частности, существование вторичной сдвиговой деформации, кривизна линий тока, сильное отклонение от локального равновесия генерации и диссипации турбулентной энергии и эффекты анизотропии турбулентности. Применение более развитых RANS моделей, в частности моделей второго порядка замыкания, разрешающих анизотропию турбулентности и восприимчивых к неустойчивостям течения, позволяет преодолеть основные недостатки моделей вихревой вязкости [2,3].

Альтернативный подход к моделированию сложных турбулентных течений, широко используемых в индустрии, основан на гибридизации RANS и LES методов [4–6]. Главная идея всех гибридных методов состоит в использовании LES подхода вдали от стенки и решении RANS уравнений в пристеночной области течения, что позволяет избежать значительных требований к сеточной детализации в пограничном слое, предъявляемых к LES методам. Гибридные методы кажутся привлекательными для моделирования закрученных ограниченных течений, так как они могут обеспечить хорошее разрешение когерентных и вторичных вихревых структур, возникающих в закрученном ядре потока. Конечно, это возможно лишь в случае достаточно детальной сетки, удовлетворяющей всем критериям разрешимости инерционного диапазона для LES методов.

Использование LES подхода для непосредственного разрешения вихревых структур в ядре течения сводит решения RANS уравнений вблизи стенки к постановке граничных условий для LES метода. Влияние статистических моделей ограничено относительно небольшим пристеночным регионом, что может объяснить применение простых одно- или двухпараметрических RANS моделей в качестве RANS ветки гибридных методов. Для описания внутренних течений со сложными каналами, особенно осложненных тепло- и массообменными процессами, при выборе пристеночной RANS модели следует обращать внимание на особенности течения. Характерные для задачи пристеночные явления требуют применения адекватной более универсальной RANS модели, содержащей в себе достаточно физики для их моделирования. С этой точки зрения лучшим кандидатом на роль RANS подмодели подходят модели второго порядка замыкания [2,3,7].

Осознание того, что URANS модели, в независимости от уровня замыкания, могут разрешить только очень крупные структуры, возникающие из-за существенных факторов, при- сущих данному течению (отрыв вихря, силы плавучести или другие массовые силы), привело к развитию адаптивных URANS моделей, обладающих повышенной чувствительностью к развитию неустойчивостей [6]. Модели этого класса строятся посредством введения в уравнения дополнительных масштабов турбулентности, представляющих высокочастотную область турбулентных пульсаций.

Один из развивающихся перспективных методов моделирования турбулентности –модель частично осредненных уравнений Навье-Стокса (Partially Averaged Navier-Stokes, PANS) [8]. В рамках данного подхода ширина фильтра осреднения пульсаций скорости контролируется заданным или определяемым в процессе расчета отношением моделируемой турбулентной энергии к полной кинетической энергии – параметром разрешения f k . Основное преимущество модели состоит в возможности разрешения длинноволновых энергонесущих структур на более грубых сетках по сравнению с сетками, необходимыми для адекватного моделирования методом крупных вихрей (LES). Этот метод должен обеспечивать разрешение минимальных возможных (при данных «сеточных условиях») масштабов. Доля разрешаемых турбулентных пульсаций приближается к возможностям LES, но сам оригинальный метод не включает в себя явным образом пространственную фильтрацию и не так строго ограничен сеточным разрешением, как LES методы.

Целью настоящей работы является построение гибридной PANS модели на основе модели второго порядка замыкания. Предложена гибридная модель, использующая зональный подход для гибридизации и модель переноса рейнольдсовых напряжений RSM SSG [9] в качестве базовой RANS модели. В пристеночной области используется URANS вариант базовой модели, а в области ядра течения вдали от стенки применяется PANS вариант модели с постоянным коэффициентом доли моделируемой турбулентной энергии – параметром разрешения. С помощью зональной PANS модели с разными значениями параметра выполнены численные расчёты нестационарного течения в отсасывающей трубе в режиме частичной нагрузки.

1.    Математическая модель

Рассматриваемая турбина типа Френсиса состоит из спиральной камеры, 14 статорных колонн, 28 лопаток направляющего аппарата, рабочего колеса с 15 полноразмерными лопастями и 15 сплиттерами и отсасывающей трубы (рис. 1) [10,11]. Для данной турбины были проведены расчёты нестационарного течения в отсасывающей трубе. Для постановки граничных условий на входе на первом этапе рассчитывали стационарное течение в части проточного тракта, включающей рабочее колесо и отсасывающую трубу. При этом область рабочего колеса моделировали в приближении «замороженного колеса» с использованием вращающейся системы отсчёта и без учёта движения лопастей рабочего колеса относительно отсасывающей трубы. На втором этапе выполняли нестационарные расчёты течения в отсасывающей трубе с граничными условиями на входе, полученными из предварительного расчёта. Для предварительных расчётов сетка состояла из 6,7 млн контрольных объемов: 3,1 млн в рабочем колесе и 3,6 млн в отсасывающей трубе. Безразмерное расстояние до стенки y+ пристеночных узлов рабочего колеса варьировалось от 10 до 100. На входе в рабочее колесо задавались постоянные тангенциальная и радиальная компоненты скорости так, что угол между вектором скорости и нормалью ко входу соответствовал углу поворота лопаток направляющего аппарата в рассматриваемом режиме (рис. 1, в).

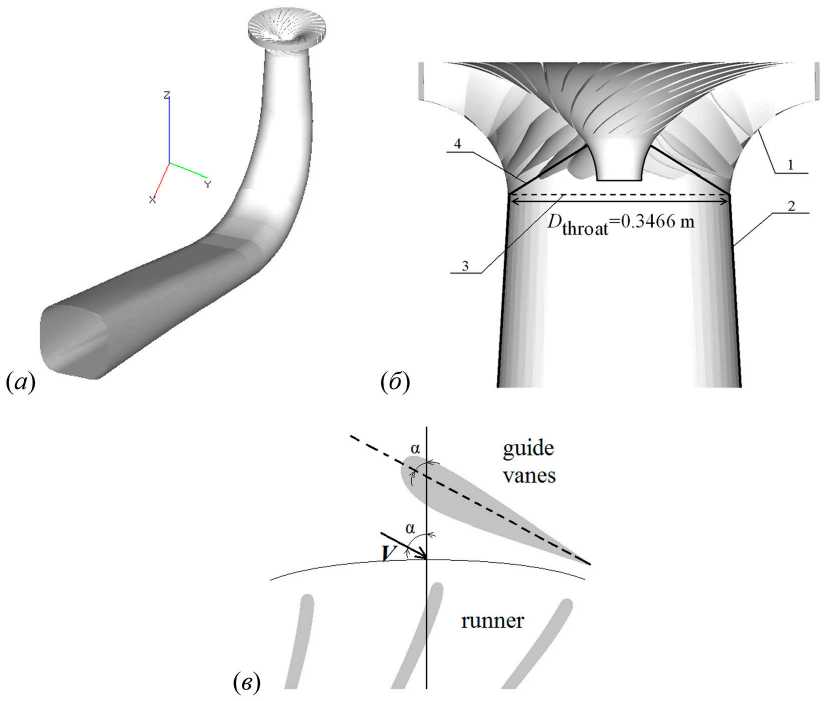
Рис. 1. Расчётная область для предварительных (стационарных) расчётов течения в турбине Francis-99 и расчётная область для нестационарных расчётов течения в отсасывающей трубе: 1– область рабочего колеса, 2 – отсасывающая труба, 3 – интерфейс, 4 – входная граница для нестационарных расчётов

Fig. 1. Computational domain for preliminary (stationary) calculations of the flow in the Francis-99 turbine and computational domain for non-stationary calculations of the flow in the suction pipe: 1 – impeller area, 2 – suction pipe, 3 – interface, 4 – inlet boundary for non-stationary calculations

Нестационарные расчёты были выполнены только для отсасывающей трубы, причём входная граница расчётной области представляла собой конус, опирающийся меньшим основанием на обтекатель рабочего колеса (рис. 1, б). На входе задавалось вращающееся с частотой вращения рабочего колеса двумерное распределение скорости, полученное из стационарного совместного расчёта ротор/отсасывающая труба.

Расчёты были проведены с использованием модели эллиптической релаксации k-8-Z-f [12], модели переноса рейнольдсовых напряжений RSM SSG [9] и гибридной RANS/ LES модели на основе k-8—Z—f. Для гибридной модели граница RANS/ LES была определена на основе предварительных URANS расчётов с помощью модели k-8—Z—f. Результаты этих исследований опубликованы в [13].

Здесь представлены численные расчёты нестационарного течения в отсасывающей трубе в режиме частичной нагрузки с помощью PANS модели турбулентности, построенной на основе модели переноса рейнольдсовых напряжений RSM SSG. В оригинальной PANS модели [8] отношения моделируемой или отфильтрованной энергии турбулентных пульсаций к полной энергии турбулентных пульсаций и соответствующее отношение скоростей диссипации турбулентной энергии произвольны (не зависят от самого решения и сетки) и постоянны во време-– 730 – ни и в пространстве. Решение PANS модели зависит от этих заданных отношений, являющихся внешними по отношению к модели параметрами.

Базовые транспортные уравнения PANS модели формулируются для моделируемой (неразрешаемой) энергии турбулентных пульсаций к и скорости её диссипации е на основе исходной RANS модели. Предполагая, что отношения этих величин к полным величинам кинетической энергии турбулентных пульсаций k tot и скорости её диссипации ε tot постоянны

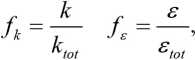
модифицируется уравнение переноса скорости диссипации исходной PANS модели:

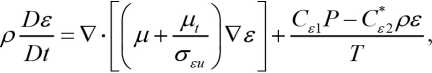
где коэффициенты модели зависят от внешних параметров модели f k и f :

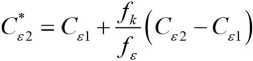
и числа Шмидта уравнений переноса турбулентных величин:

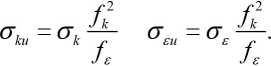
На практике для моделирования высокорейнольдсовых течений параметр f приравнивается к единице. Исходная PANS модель предполагает постоянство параметра f_k , лежащего в диапазоне от нуля до единицы. Когда параметр разрешения f k стремится к нулю, численное решение эффективно соответствует прямому численному моделированию турбулентности. Если параметр разрешения стремится к единице, решение PANS модели соответствует решению исходной RANS модели. В целом ряде работ показано, что в случае моделирования течений с крупномасштабными неустойчивостями переход к PANS модели позволяет улучшить результат по сравнению с базовой RANS моделью [14,15]. А важной особенностью PANS подхода является меньшая по сравнению с методами крупных вихрей (LES) зависимость от сеточной детализации [16].

На основе RSM SSG модели разработана зональная PANS модель. Расчётная область разбивается на две зоны - пристеночную и «свободную» (или область вдали от стенки). В пристеночной области применяется исходная (U)RANS модель, в «свободной» - PANS версия с постоянным параметром разрешения f k = const меньше единицы.

Положение границы пристеночной области определятся на основе предварительного стационарного RANS расчёта с помощью модели вихревой вязкости. В пристеночной области выполняется требование А >  L t /10, где А - шаг сетки, L t = к ^3/2/е - турбулентный масштаб крупных энергонесущих вихрей. Положение интерфейса в процессе расчёта не меняется. Выполнены расчёты с тремя значениями параметра разрешения f_k = 1, 0.6, 0.4 в «свободной» области. PANS модель с параметром разрешения f k = 1 соответствует исходной RANS RSM модели.

2.    Результаты

Сравнение результатов расчёта проводили с экспериментальными данными [10,11], которые представляют собой распределение аксиальной и тангенциальной компонент скорости и их пульсаций в двух сечениях в отсасывающей трубе.

На рис. 2 показаны расчётные и экспериментальные профили скорости в отсасывающей трубе для режима частичной нагрузки. Модель RSM в целом хорошо воспроизводит профили компонент скорости, в том числе реалистичный профиль тангенциальной компоненты скорости. Расчёты с разными значениями параметра разрешения дают практически неотличимые результаты. Небольшое улучшение при уменьшении параметра разрешения наблюдается в ядре течения в нижнем сечении.

На рис. 3 показаны среднеквадратичные пульсации аксиальной и тангенциальной компонент скорости. В верхнем сечении все модели недооценивают уровень турбулентных пульсаций, что, по-видимому, связано с недостатками постановки граничных условий на входе. Все модели корректно предсказывают два пика пульсаций в сдвиговом слое. Увеличение разрешаемой части энергии пульсации (уменьшение параметра разрешения) немного улучшает предсказание уровня пульсаций скорости в сдвиговом слое при r ~ 120 мм.

В нижнем сечении численные результаты хорошо соответствуют экспериментальным данным. Исходная RSM модель недооценивает уровень пульсаций тангенциальной компоненты скорости в центре и слегка переоценивает уровень пульсаций аксиальной компоненты

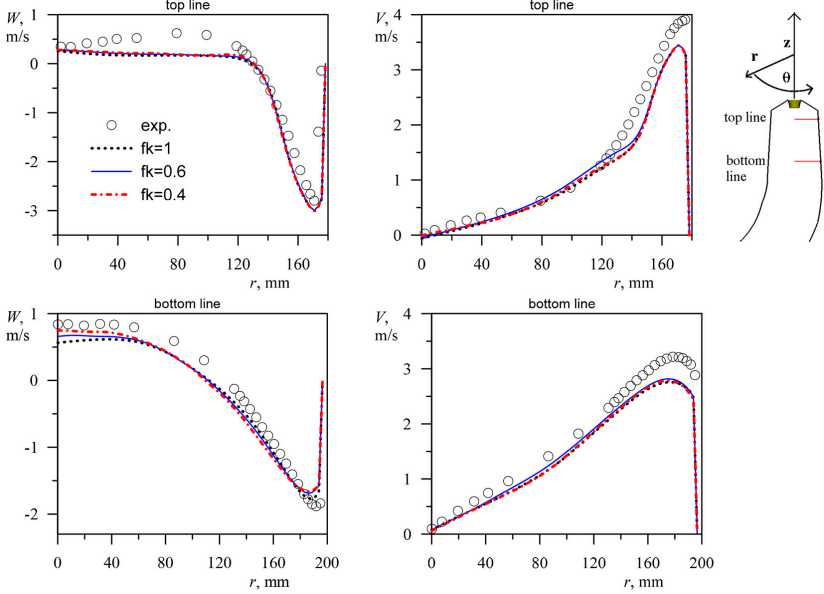
Рис. 2. Радиальное распределение средних аксиальной и тангенциальной компонент скорости

Fig. 2. Radial distribution of the average axial and tangential velocity components

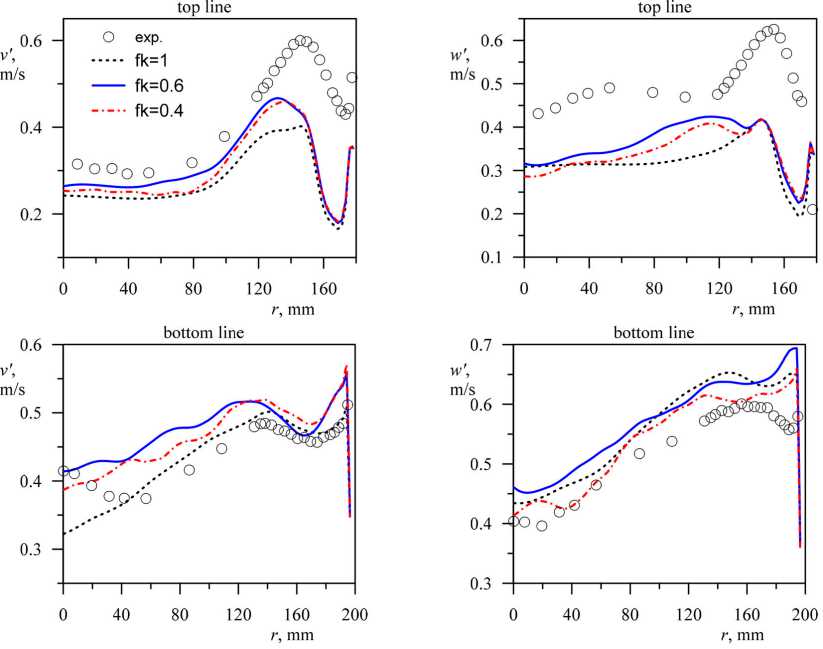
распределение среднеквадратичных пульсаций аксиальной и тангенциальной

Рис. 3. Радиальное компонент скорости

Fig. 3. Radial distribution of root-mean-square fluctuations of the axial and tangential velocity components скорости в сдвиговом слое. Уменьшение параметра разрешения приводит к повышению предсказываемого уровня пульсаций тангенциальной компоненты в ядре течения при r < 40 мм и уменьшению пульсаций аксиальной компоненты в сдвиговой области при r ~ 120–160 мм. В целом переход к PANS версии модели позволяет улучшить согласование с экспериментальными данными по пульсациям скорости.

На рис. 4 представлены профили кинетической энергии турбулентных пульсаций и численно получаемой доли моделируемой энергии турбулентных пульсаций, которая рассчитывается на основе собранной статистки:

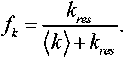
PANS варианты модели приводят к увеличению уровня пульсаций скорости в сдвиговом течении в верхнем сечении и в ядре течения в нижнем сечении. Как и ожидалось, уменьшение параметра разрешения или «требуемой» доли моделируемой турбулентной энергии понижает численно реализующуюся долю моделируемой турбулентной энергии. Вдали от стенки распределение доли моделируемой турбулентной энергии относительно монотонно. Значения этого параметра лежат в следующих диапазонах в зависимости от параметра разрешения модели:

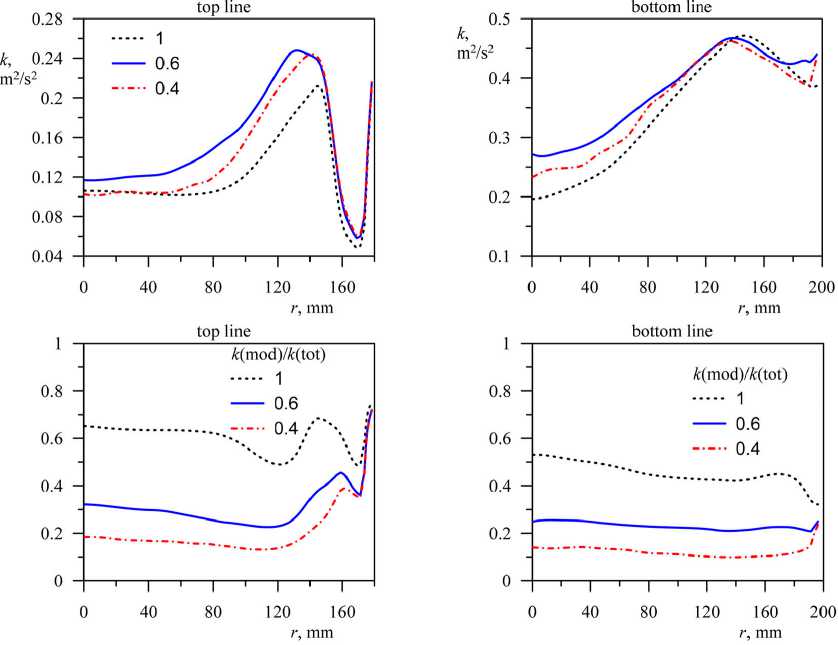
Рис. 4. Радиальное распределение полной кинетической энергии турбулентных пульсаций и расчётной доли моделируемой турбулентной энергии

Fig. 4. Radial distribution of the total kinetic energy of turbulent fluctuations and the calculated fraction of the simulated turbulent energy при fk = 1 – (0.4–0.6), при fk = 0.6 – (0.2–0.4) и при fk = 0.4 – (0.1–0.2). Задание параметра разрешения при fk = 0.4 практически приводит к LES-подобному моделированию, при котором доля разрешаемой энергии турбулентных пульсаций превосходит 80 %.

Сложная система вихрей, обнаруженная в отсасывающей трубе данной турбины в режиме частичной нагрузки, представляет интерес и с научной, и с практической точек зрения, поскольку она перераспределяет энергию течения, приводит к потерям энергии и генерирует интенсивные пульсации давления.

Рис. 5 демонстрирует особенности течения и вихревых структур, полученные с помощью трёх рассмотренных вариантов модели. Визуализация с помощью критерия λ ₂ показывает спиральные вихревые структуры, охватывающие центральную часть течения. В зоне подъемного течения находится широкий центральный вихрь с близким к твердотельному вращением жидкости. Сильно закрученный опускной поток вблизи стенки насыщен множеством спиральных вихревых структур.

Модель RSM (PANS c f k =1) обнаруживает большую восприимчивость к неустойчивости, показывая крупномасштабные спиральные вихревые структуры. Сразу за рабочим колесом в пристеночном сдвиговом слое между опускным и подъемным течением развивается несколь- – 734 –

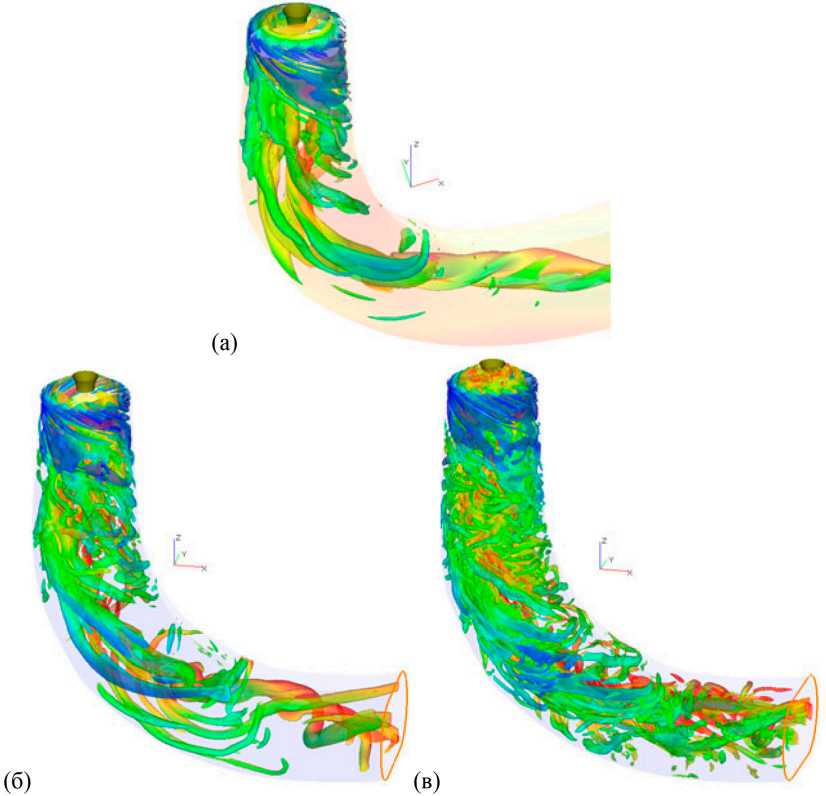
Рис. 5. Структура течения в отсасывающей трубе в режиме частичной нагрузки: мгновенные вихревые структруры, визуализированные с помощью изоповерхности λ2 критерия (цветом также показана аксиальная компонента скорости): а) fk =1; б) fk =0,6; в) fk =0,4

Fig. 5. The structure of the flow in the suction pipe in the partial load mode: instantaneous vortex structures visualized using the isosurface Z2 criterion (the axial velocity component is also shown in color): a) fk =1; b) fk =0.6; c) fk =0.4

ко протяженных крупномасштабных вихрей. Их образование происходит путем слияния вихревых структур, сходящих с лопастей рабочего колеса. Эти вихри сворачиваются в спиральные жгуты и вращаются вокруг зоны подъемного течения. В каждый момент времени наблюдается четыре или пять подобных структур. Ниже по течению колена отсасывающей трубы эти структуры преобразуются в один прецессирующий вихрь (рис. 5а).

Увеличение требуемой доли разрешаемой турбулентной энергии ожидаемо приводит к увеличению разрешаемого диапазона пространственных масштабов вихревых структур. PANS варианты модели показывают характерную для метода моделирования крупных вихрей картину течения (рис. 5 б, в), разрешая структуры в широком диапазоне масштабов, среди которых можно выделить крупномасштабные когерентные структуры.

Изменение масштабов разрешаемых вихревых структур хорошо отслеживается на графике спектра пульсаций в выбранной точке, показанном на рис. 6. Здесь частоты отнормированы

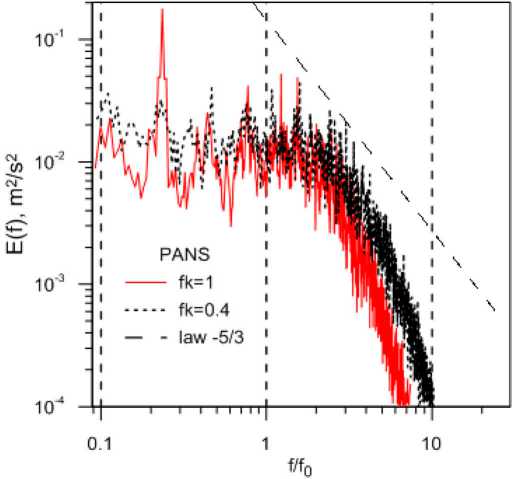
Рис. 6. Спектральная плотность мощности пульсаций скорости

Fig. 6. Power spectral density of velocity pulsations на частоту вращения рабочего колеса f0. В области низких частот < 2f0 (или, соответственно, крупных линейных масштабов) преобладает линейчатый спектр, в области частот выше 2f0 спектр пульсаций скорости близок к сплошному. Увеличение требуемой доли разрешаемых масштабов пульсаций (уменьшение fk) приводит к уменьшению пиков пульсаций в низкочастотной области, увеличению амплитуды пульсаций в высокочастотной области и насыщению высокочастотного хвоста спектра пульсаций. При переходе от fk= 1 к fk = 0.4 интенсивность пульсаций крупных вихрей уменьшается, увеличивается диапазон разрешаемых турбулентных вихрей и лучше разрешается каскадный механизм переноса энергии пульсаций.

Выводы

В целом приведенные результаты расчётов с зональной PANS RSM модели позволяют сформулировать следующие выводы. К достоинствам модели можно отнести возможность увеличения диапазона разрешаемых масштабов, вплоть до масштабов инерционного интервала, в зависимости от сеточной детализации. Использование в качестве базовой наиболее физически обоснованной модели, а именно дифференциальной модели переноса турбулентных напряжений, радикально улучшает предсказательность модели для сильно анизотропных течений. Базовая RANS модель имеет высокую чувствительность к неустойчивостям закрученного течения и проявляет вихреразрешающие способности. Отсутствие необходимости разрешать вихревые структуры инерционного интервала приводит к меньшим требования к сеточной детализации по сравнению с моделями крупных вихрей LES и, как следствие, требует меньших вычислительных ресурсов и снижает время подготовки и построения сеточной модели. PANS подход в рассмотренной реализации не содержит явной зависимости от шага пространственной сетки.

Вместе с тем следует отметить и недостатки рассмотренного подхода. PANS модель наследует недостатки базовой RANS модели, прежде всего увеличенные по сравнению с моделями вихревой вязкости вычислительные затраты из-за большего числа уравнений переноса. Расширение спектра разрешаемых пульсаций приводит к увеличению времени для сбора статистики.

К существенным недостаткам отнесем и некую произвольность выбора параметра разрешения, который в данном подходе задаётся однородным и постоянным вне зависимости от сеточной детализации. Параметр разрешения должен быть согласован с получаемым численным решением и сеточным разрешением. В дальнейшем предполагается рассмотреть вариант PANS модели с динамическим параметром разрешения турбулентности, зависящим от локального характера течения.