Применение подхода Лагранжа к решению одномерной задачи распространения волн в газе в рамках применимости адиабатического закона

1. МАТЕМАТИЧЕСКАЯ

ФОРМУЛИРОВКА ЗАДАЧИ где P (смотри [2]) определяется следующим об- разом

Уравнения, описывающие одномерную задачу линейной акустики, получаются из уравнений Навье-Стокса при отбрасывании конвекционных и вязких членов. Закон изменения давления считается адиабатическим, в результате в размерных переменных будем иметь [1]

P = fcd ₽ р ^,

тогда систему (2) можно привести к системе уравнений, аналогичных уравнениям конвекции (переноса) [2]

др* . д u *

+ Р — =0 0

д t *        дх*      ’

д Wj д t

д w 1 д х

= 0

д u * c *2 др * д t * р * д х *

= 0

.

д w,   д w,

---- - c--- 2 д t      д х

= 0

Здесь u * — скорость, р * - плотность, х * — координата, t * — время, _c*2 = kp * /р * — квадрат скорости звука, p^* – давление, k – показатель адиабаты.

Введя следующие безразмерные переменные: u = u * /u₀ , р = р * / р ₀ , х = x */ b , t = t * b/u₀ , c = c / u₀ , где b - характерный размер, u₀ -

характерная скорость, р ₀ - характерная плотность, система уравнений (1) примет безразмерную форму[1]

др   д u А р = 0 д t    д х

д u c² др _А

— +-- = 0 0

д t р д х

Сделаем следующую замену переменных w_J = u + P , w₂ = u - P ,    (3)

Здесь мы будем считать, что плотность в волне сжатия изменяется по закону изоэнтропической адиабаты, а не ударной адиабаты. Данный подход справедлив [2], если плотность газа в волне сжатия возрастает не более чем в два раза по сравнению с невозмущенным газом. В случае изоэнтропической адиабаты равенство (4) приобретает вид

2c — p = г-г(р2 — J).        (6)

k - J

Система (5) не имеет аналитического решения, но ее можно решить [2] методом характеристик. Если задано начальное распределение значений u и P, то на следующем слое эти величины находятся как

^u(t,x) = 2 [ ^WJ ( ^t0^,Xi ) ^{+ W}2 ( ^t0^,Xi + J ) ] ,

^P ( ^t,x ) = 2 [ W J ( ^t0^,Xi ) ^- W 2 (t o^,xi + J ) ] ,     (7)

где

h t = t0 +           х = х + ci(t -t0) . (8)

^ci ^{+ c}i + i ,

Здесь h – шаг однородной сетки, t₀ - начальный момент времени. Решение, полученное с помощью метода характеристик, мы будем использовать в качестве тестового.

• 2.    ЧИСЛЕННЫЕ СХЕМЫ

• 2.1.    Применение метода Годунова для решения уравнений нелинейной акустики

ПРИМЕНЯЕМЫХ МЕТОДОВ

Хотя в книге [3] метод Годунова для решения задач нелинейной акустики не описан, здесь мы рассмотрим применение его подхода для линейных задач, адаптированного под нелинейную задачу.

В методе Годунова [3] используется “шахматная” сетка, когда в центрах ячеек определяются “малые” переменные, а на границах ячеек – “большие” переменные. Значения величин плотности и скорости в следующий момент времени при применении метода Годунова находятся как

j        j-1 A tc      j-1j w1i = w1i -- (w1i - w1i-1), h j         j-1      tc       j-1j w2i = w2i      h (w'''l - w2i ) .(12)

ГУ на стенке накладываются согласно (11), после чего они подставляются в (3).

2.3. Применение подхода Лагранжа для решения уравнений нелинейной акустики в форме конвективных уравнений

Систему уравнений (5) можно также решить с применением подхода Лагранжа к рассмотрению движения среды. Здесь предлагается использовать метод, применяемый для моделирования конвекции в методе “вихрь в ячейке” (ВЯ) [4]. При этом моделируется движение двух волн. Одна распространяется вправо и переносит величину w₁ . При этом в следующий момент времени

p i = P i ¹

^^^^^^^^

At ( TJj ¹ , (U i + 0.5 h

^^^^^^^в

U ¹ 1 U i - 0.5 )   ,

* ^j           j - 1

^w1i = ^w1i   ,

x i = x i ^{- 1 +} c Д t .      (13)

u j = u i ¹ - ^A

tc2

h p

(R i - 0.5

- Ri^) ,

где _д t — шаг по времени,

■ j^- i + 0.5

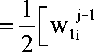
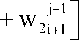
A k - 1

j - i + 0.5

pI

^Г i+ 0.5

I

k - 1

+ 1

)

> j-1

i + 0.5

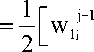
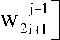
а w₁ и w₂ - находятся с помощью (3).

Если центр ячейки i+1 находится “внутри” тела, то граничные условия (ГУ) на стенке определяются следующим образом:

u i - =- u i ^{- 1} .      p i + 1 =p i ^{- 1} .         (11)

При этом ГУ (11) подставляются в (3), а потом (3) подставляются (10).

2.2. Применение схемы вперед по потоку для решения уравнений нелинейной акустики в форме конвективных уравнений

К системе уравнений (5) удобно применить конечно-разностную схему вперед по потоку (ВП), в результате будем иметь

Другая волна распространяется влево и переносит величину w₂ , причем

w 2i = w₂ i ^{- 1} , x i = x i ^{- 1} - c _д t . (14)

Здесь w₁^*_i^j и w^*_2i^j обозначают величины w₁ и w₂ на искаженной после перемещения сетке. Для того, чтобы получить величины w₁ и w₂ на основной однородной сетке, аналогично методу ВЯ производится процедура перераспределения новых значений в ячейки сетки

^w1k = ^w*i ^{л (x}k ^{- 1 -} x i ) , ^w2k = ^w2i ^{л (x}k ^{- 1} - x i ) ,

где в качестве интерполяционной функции Л предлагается использовать кусочно-постоянное

или кусочно-линейное распределение

^Л 1^(z)

| 1 -I z/h|

1     0,

|z/h| <  1

|z/h| >

, (16)

Рассмотрим ГУ на стенке для правой волны. Если ячейка при своем движении (13) оказывается “внутри” тела, то она “отражается” от его поверхности, и ее координата определяется как x j = 2x b - x i - c д t ,          (18)

где x_b – координата стенки тела. При этом правая волна превращается в левую волну и в точке с координатой (18) оказывается уже величина

U = 0

w₂ j =- u j ^{- 1} - P ij ^{- 1} . (19)

Равенство (19) получается при подстановке ГУ (10) в выражения (3). После чего полученная величина (19) перераспределяется в ячейки расчетной сетки согласно (15), (16) или (15), (17). ГУ на стенке для левой волны получается аналогично.

3. ТЕСТИРОВАНИЕ МЕТОДОВ

Описанные выше четыре численных схемы тестировались на трех задачах, отличающихся начальными условиями (НУ) и ГУ.

В первой тестовой задаче НУ соответствуют однородному потоку u0 = 1, Р0 = 1, (20) а в момент времени t > 0 в точке x = 0 ставится непроницаемая перегородка.

НУ второй тестовой задачи задавались следующим образом:

Р 0

= <

• 1,    x < 0.5

  • 1.2,    x > 0.5’

твердые границы отсутствовали.

В третьей тестовой задаче твердые границы также отсутствовали, а НУ задавались как

u0 = <

1, 0.4 < x < 0.6

0, x < 0.4 U x > 0.6’

p ⁰ = 1 .                                (22)

В тестовых расчетах использовались конечные области. В первой задаче область принималась равной x g [ - 1,1 ] , а во второй и третьей задачах области имели вид x g [ 0,1 ] .

Численное решение сравнивалось с решением методом характеристик (7), (8). В результате

расчетов выяснилось, что наилучшие результаты для первых двух рассмотренных методов получаются, если шаг по времени удовлетворяет выражению

h

Д t = k a----

, max

называемому критерием Куранта-Фридриха-Леви [5], с величиной коэффициента k a = 1 . Заметим, что для предложенной схемы, использующей подход Лагранжа, можно варьировать шагом по времени, и наилучшие результаты получаются, когда k_a – ограниченное натуральное число.

Результаты, показанные на рис. 1-6, получены после 20 шагов по времени ( t = 5.76195268 - 10^-4 ) для С = 347.105 , h = 0.01 . В некоторых случаях графики результатов, получаемые с помощью разных методов,

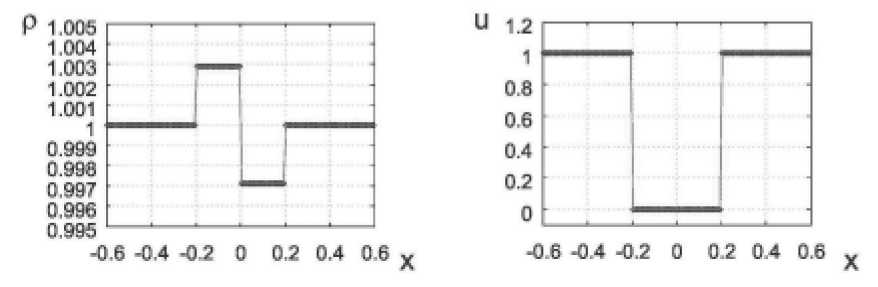
Рис. 1. Распределение плотности и скорости в задаче (20) для всех рассмотренных методов: – численное решение, – аналитическое решение

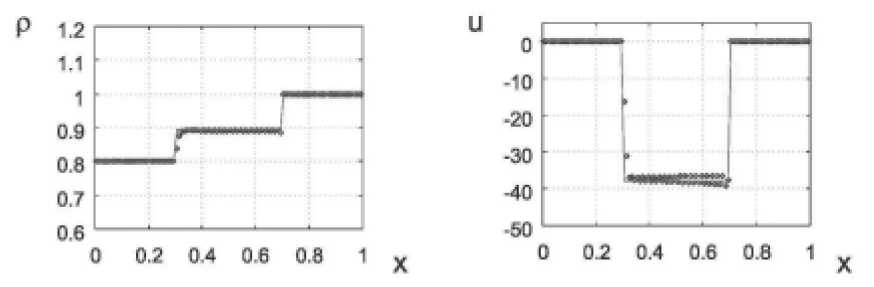
Рис. 2. Распределение плотности и скорости в задаче (21) для метода, использующего схему Годунова: – численное решение, – аналитическое решение

Рис. 3. Распределение плотности и скорости в задаче (21) для метода, использующего ВП схему:

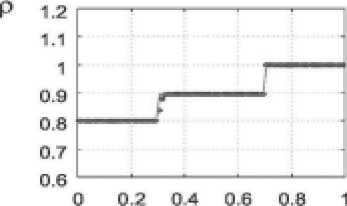
о – численное решение, – аналитическое решение

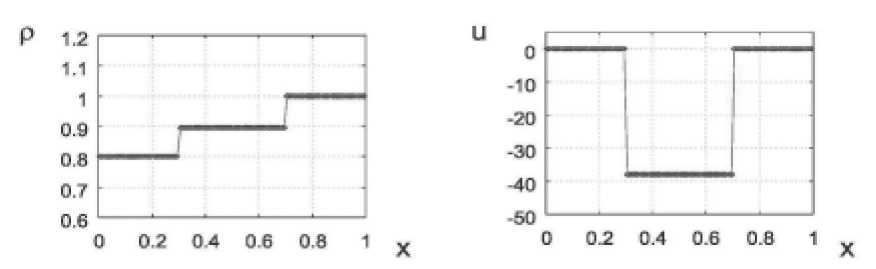
Рис. 4. Распределение плотности и скорости в задаче (21) для метода, использующего подход Лагранжа с распределением (16): о – численное решение, – аналитическое решение

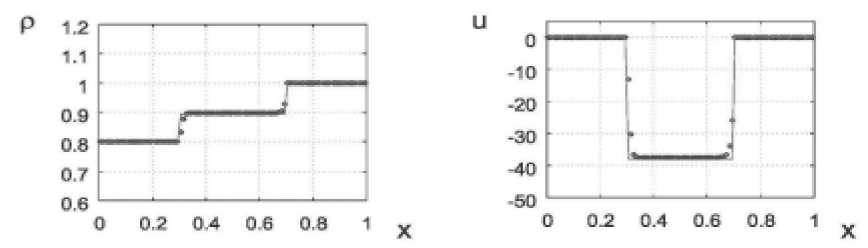
Рис. 5. Распределение плотности и скорости в задаче (21) для метода, использующего подход Лагранжа с распределением (17): о – численное решение, – аналитическое решение

визуально не отличаются, поэтому они приведены один раз. Заметим, что на графике скорости на рис. 2 наблюдается два ряда чередующихся точек. Это указывает на “пилообразный” характер решения.

Погрешность решения определялась следующим образом:

δ

u

=max

x

ui

-

u char

u char

⋅100 %,

где uchar – значение скорости, полученное методом характеристик. Заметим, что для задачи (20) максимальная погрешность наблюдается в зоне нулевой скорости. В этом случае, чтобы избежать деления на ноль в формуле (24), ее знаменатель принимался равным единице.

Ошибка численного решения (24) после 20 шагов по времени ( k_a =1) представлена в табл. Из анализа табл. видно, что наибольшую точность имеет метод, использующий подход Лагранжа с распределением (16). Худшие результаты метода, использующего подход Лагранжа с распределением (17), объясняется большой численной диффузией данного перераспределения. Значительный рост погрешности в задаче (21) объясняется тем, что при таких начальных данных начинает сказываться нелинейность задачи (изменения плотности и скорости).

Для предложенной в настоящей работе схемы, использующей подход Лагранжа, проводилось моделирование данных задач для k_a равных 1, 2, 4 и 20. При этом средняя погрешность

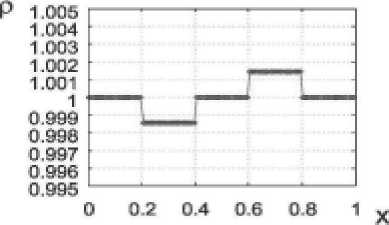
Рис. 6. Распределение плотности и скорости в задаче (22) для всех рассмотренных методов:

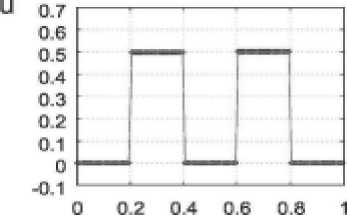
о – численное решение,

– аналитическое решение

Таблица. Максимальная погрешность решения рассмотренных задач, полученного различными методами численного решения уменьшается при увеличении k . Это объясняется меньшим количеством a выполняемых арифметических операций (в том числе и перераспределения в ячейки сетки).

В заключение можно сделать следующие выводы:

• 1)    Метод, использующий подход Лагранжа с распределением (16), адекватно моделируют распространение волн в одномерных задачах нелинейной акустики в рамках применимости адиабатического закона.

• 2)    Предложенный метод позволяет варьировать в широких пределах шагом по времени.