Применение полносвязной искусственной нейронной сети для прогнозирования режимов хранения отечественного низкомасличного сырья в контролируемых средах

В настоящее время остро стоит проблема развития импортозамещающих технологий, рационального использования отечественных сырьевых ресурсов, в этой связи переработка вторичных фракций зародышей пшеницы (ЗП) представляет интерес. Создание на их основе пищевых продуктов с прогнозируемым биопотенциалом и потребительскими свойствами, является важным и перспективным направлением развития пищевой промышленности страны.

ЗП обладают низкой стабильностью при хранении (рисунок 1). С целью разработки практических рекомендаций по режимам хранения ЗП были выбраны интервалы варьирования факторов (таблица 1). Воспользовавшись программой обучения и анализа обучения искусственной нейронной сети (ИНС) на языке Python 2.7 с программными библиотеками математической обработки научных данных «scipy», разработали программный продукт, с помощью которого экспериментальные данные были обработаны.

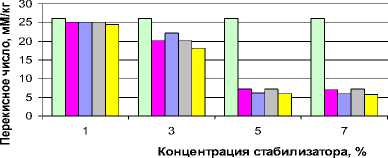
□ Контроль

□ Смесь III

□ Смесь I

□ Смесь IV

□ Смесь II

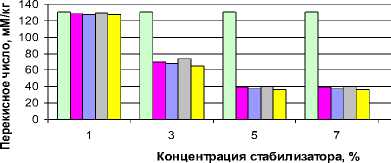
□ Контроль      □ Смесь I

□ Смесь II

□ Смесь III

□ Смесь IV

б

Рисунок 1. Значения перекисных чисел на 8 неделе хранения зародышей пшеницы, обработанных композициями органических кислот: а – холодильник; б – склад

Для работы была выбрана полносвязная нейронная сеть. В качестве входных параметров нейронной сети рассматривали: влажность пшеничных зародышей (х1, %), относительную влажность окружающего воздуха (х2, %), температуру окружающей среды (х3, ºС) и концентрацию смеси органических кислот (х4, %). Сеть будет иметь один выход – значение пере- кисного числа (у, мМ/кг). Время хранения считалось постоянным (8 недель). При определении диапазона изменения факторов интервалы измерений устанавливались таким образом, чтобы нужные нам величины располагались внутри интервала (таблица 1).

Т а б л и ц а 1

Интервалы варьирования входных параметров нейронной сети

Факторы	Единица измерения	Интервал варьирования
		Нижний предел	Верхний предел
Влажность зародышей пшеницы	%	14	16
Относительная влажность окружающего воздуха	%	60	80
Температура окружающей среды	ºС	0	28
Концентрация стабилизатора	%	1	7

Искусственная нейронная сеть (ИНС) - математическая модель, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма. Нейронные сети позволяют решать очень большой круг практических проблем, в частности, классификаций. Задача, решаемая в проведенных исследованиях, в представленном виде не является задачей классификации, но может быть сведена к ней [1, 2, 3].

При осуществлении функционирования нейрон одновременно принимает множество входных сигналов. Каждый вход нейронной сети обладает своим личным синоптическим весом, который оказывает влияние на него и необходим для функции сумматора. Вес считается мерой значимости входных связей. Весы влиятельного входа увеличиваются и, наоборот, вес несущественного входа принудительно сокращается, что характеризует силу входного сигнала. Весы могут меняться в соответствии с обучающими примерами, в качестве которых используются значения перекисных чисел на 8 неделе хранения зародышей пшеницы, стабилизированных комплексами органических кислот. Также влияние оказывает архитектура сети и правила обучения. Первым действием нейрона считается расчет взвешенной суммы всех входов, в результате будет получено одно число. Результат функции сумматора проходит через передаточную функцию и преобразуется в выходной сигнал. В передаточной функции для выявления выхода нейрона общая сумма сверяется с некоторым порогом. Если сумма

Вестник ВГУИТ, №3, 2015 больше значения порога, нейрон генерирует сигнал, в противном случае сигнал будет нулевым или тормозящим [4].

Далее после передаточной функции выходной сигнал проходит дополнительную обработку масштабирования, то есть результат передаточной функции множится на масштабирующий коэффициент и добавляется смещение. По аналогии с биологическим нейроном, каждый искусственный нейрон имеет один выходной сигнал, который передается множеству других нейронов. В основном, выход прямо пропорционален результату передаточной функции. В некоторых сетевых архитектурах результаты передаточной функции изменяются для создания соревнования между соседними нейронами. Нейронам предлагается соревноваться между собой, блокируя действия нейронов, имеющих несильный сигнал. Конкуренция может происходить между нейронами, расположенными на одном или разных слоях. Во-первых, конкуренция определяет, какой искусственный нейрон будет активным и обеспечит выходной сигнал. Во-вторых, конкурирующие выходы помогают выяснить, какой нейрон будет участвовать в процессе обучения [3-5].

Целью обучения является настраивание весов соединений на входах каждого нейрона в соответствии с заданным алгоритмом обучения для получения требуемого результата. Существует два способа обучения: контролируемое и неконтролируемое. В случае неконтролируемого обучения система самоорганизовывается по внутреннему критерию, заложенному в алгоритм обучения. Контролируемое обучение (применяемое в нашем случае) требует обучающего множества данных или наблюдателя, который отслеживает эффективность результатов сети.

Среди известных архитектурных решений выделяют группу слабосвязанных нейронных сетей, в которой нейроны связаны лишь со своими соседями, и полносвязные сети (применяемые в нашем случае), в которых нейроны связаны по принципу “каждый с каждым”.

Анализируя наиболее известные на данное время разработки нейронных сетей, необходимо отметить, что самым распространенным вариантом архитектуры являются многослойные сети с прямым распространением. Нейроны в данной архитектуре объединяются в структуры под названием слои, у которых существует один вектор входов. Внешний набор входов называется рецепторами, а внешний набор выходов из последнего слоя называются эффекторами. Между наборами входов и выходов имеется некоторое количество слоев [5].

Далее, для исследования зависимости перекисного числа речь будет идти исключительно про полносвязанные нейронные сети. На рисунке 2 представлен результат обучения нейронной сети, где по оси абсцисс расположены значения количества слоев, по оси ординат – ошибка обучения. Несложно увидеть, что минимальная ошибка соответствует сетям с количеством слоев 2 и 4 (рисунок 2).

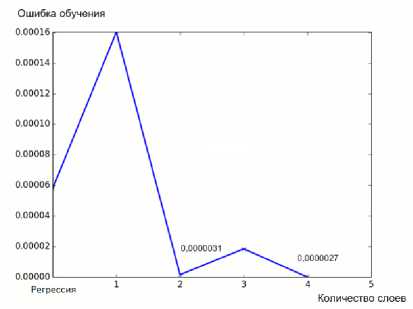
Рисунок 2. Зависимость ошибки обучения от количества слоев нейронной сети

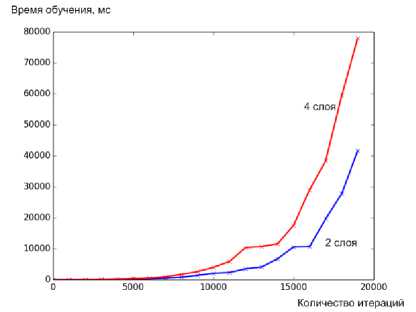
Рисунок 3. Зависимость времени обучения в миллисекундах от количества итераций:

красный график – нейронная сеть с 4 слоями, синий график – нейронная сеть с 2 слоями

Особенность нейронных сетей, как аналога биологического мозга, состоит в способности к обучению ”с учителем”, что означает наличие исходного обучающего множества. Обучение нейронной сети в данном контексте рассматривается как синтез и анализ архитектуры и весовых коэффициентов нейронных связей в соответствии с данными обучающего множества для решения проблемы. Наличие экспериментальных данных в этой работе позволяет использовать режим контролируемого обучения.

С помощью программного обеспечения были спроектированы и обучены несколько нейронных сетей. По результатам обучения выбранные сети необходимо протестировать на скорость работы. Результаты исследования представлены на рисунке 3. Очевидно, что для моделирования следует использовать сеть с двумя слоями, как наиболее “быструю” с точки зрения эффективности использования машинного времени и ошибки обучения (рисунок 2).

Коэффициенты выбранной нейронной сети представлены на рисунке 4.

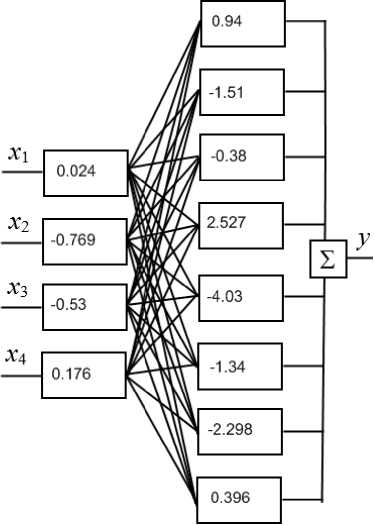
Рисунок 4. Выбранная архитектура нейронной сети, где х₁ - влажность пшеничных зародышей, %; х₂ - относительная влажность окружающего воздуха, %; х з - температура окружающей среды, °С; х₄ - концентрация стабилизатора; у - значение перекисного числа, мМ/кг

Результат работы ИНС представлен на рисунках 5, 6.

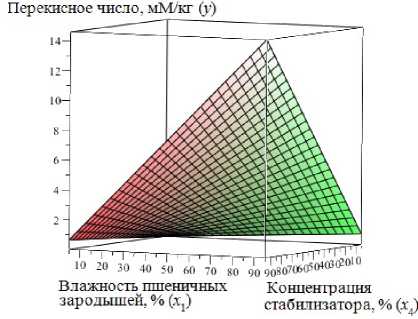
Рисунок 5. Результат работы нейронной сети с зафиксированными входными параметрами (x 2 = 60, %, х з = 20, °C): два вида одной трехмерной поверхности, построенной как y (x i , Х 4 )

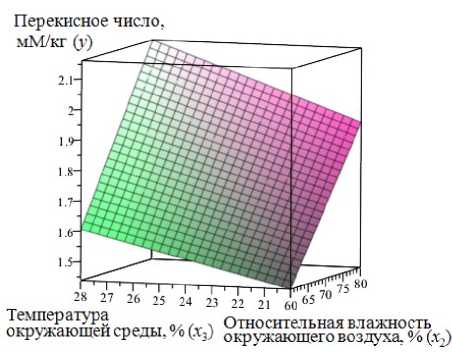
Рисунок 6. Результат работы нейронной сети с зафиксированными входными параметрами (x₁=15 %, Х 4 =5 %): два вида одной трехмерной поверхности, построенной как y(x 2 , х з )

Применяя разработанную и обученную нейронную сеть, можно построить зависимость у (х 1 , х 2 , х з , х д ) - это пятимерное пространство, которое сложно визуализировать. Для визуализации в трехмерном пространстве необходимо ограничить количество аргументов функции двумя. На рисунке 5 представлен результат работы нейронной сети y (x i , Х 4 ) с зафиксированными входными параметрами (х 2 = 60, %, х з =20, °C). На рисунке 6 представлен результат работы нейронной сети у (х 2 , х з ) с зафиксированными входными параметрами (х 1 = 15 %, х 4 = 5 %).

В результате работы получили обученную нейронную сеть, которая по заданной совокупности значений влажности пшеничных зародышей, относительной влажности окружающего воздуха, температуры окружающей среды и концентрации смеси органических кислот позволяет получить конкретное значение выходного параметра - перекисного числа [5, 6]. В результате подстановки различных значений параметров х 1 , х 2 , х з , х 4 можно сделать вывод, что при самых неблагоприятных условиях хранения пшеничных зародышей в складе (относительная влажность воздуха 80 %, температура 28 ºС) минимально возможное значение стабилизирующей смеси составляет 5 %, при этом значение перекисного числа изменяется в допустимых пределах. Данная математическая модель позволяет с высокой точностью получать значения концентрации стабилизирующей смеси в зависимости от конкретных условий и планировать режимы хранения в контролируемых средах [5, 7, 8].